[机器学习] Coursera笔记 - Support Vector Machines

Posted 2022-12-08 WangBo_NLPR

序言

　　机器学习栏目记录我在学习Machine Learning过程的一些心得笔记，包括在线课程或Tutorial的学习笔记，论文资料的阅读笔记，算法代码的调试心得，前沿理论的思考等等，针对不同的内容会开设不同的专栏系列。
　　机器学习是一个令人激动令人着迷的研究领域，既有美妙的理论公式，又有实用的工程技术，在不断学习和应用机器学习算法的过程中，我愈发的被这个领域所吸引，只恨自己没有早点接触到这个神奇伟大的领域！不过我也觉得自己非常幸运，生活在这个机器学习技术发展如火如荼的时代，并且做着与之相关的工作。
　　写博客的目的是为了促使自己不断总结经验教训，思考算法原理，加深技术理解，并锻炼自己的表述和写作能力。同时，希望可以通过分享经验帮助新入门的朋友，结识从事相关工作的朋友，也希望得到高人大神的批评指正！
　　
　　
　　

前言

　　[机器学习] Coursera笔记系列是以我在Coursera上学习Machine Learning（Andrew Ng老师主讲）课程时的笔记资料加以整理推出的。内容涵盖线性回归、逻辑回归、Softmax回归、SVM、神经网络和CNN等等，主要学习资料来自Andrew Ng老师在Coursera的机器学习教程以及UFLDL Tutorial，Stanford CS231n等在线课程和Tutorial，同时也参考了大量网上的相关资料。
　　
　　本文主要整理自“Support Vector Machines (SVMs)”课程的笔记资料和一些经典教材，同时也参考了网上经典的关于SVM的博客（后面会列出）。由于Ng讲解的SVM实在是简单的不能再简单了，与传统的SVM Tutorial相差太多，很多细节甚至没法深入推敲……我估计很多同学在学习该课程时候都会产生大量的疑问，所以本文并不对Ng的SVM课程知识结构做梳理（因为实在是简单的都变形了，大量重要知识点都被略过），而是给出课程中每个知识点与常规SVM Tutorial进行对比，希望能给读者一个思路。
　　
　　文章小节安排如下：
　　1）SVM的基本思想
　　2）优化目标（Optimization Objective）
　　3）假设函数与决策边界（Hypothesis Function And Decision Boundary）
　　4）什么是支持向量
　　5）核函数（Kernels Function）
　　6）最后的总结
　　
　　

零-1、关于Ng的SVM课程

　　Ng老师在Coursera的SVM课程实在是简单的不能再简单了，课程所讲的SVM甚至有点变形了，很多同学在学习Coursera Ng SVM这一章时候都会产生大量疑问…………等读者接触了更多的SVM资料就会发现，Ng老师为了让我们更好的入门SVM，为了消除我们对SVM理论的恐惧感，为了建立我们的信心，真的是将SVM理论简化的不能再简化了……没有VC维，没有结构风险概念，没有SMO算法，没有KKT条件，没有拉格朗日……SVM严谨漂亮的数学被Ng老师全都略去了……
　　
　　要知道微软的SVM Tutorial中第一段是这样说的：
　　The tutorial starts with an overview of the concepts of VC dimension and structural risk minimization.
　　
　　大部分教材的基础部分会复习一下函数间隔和几何间隔，然后从最大化间隔思想推导出SVM的优化目标，进而会讲解支持向量是什么，硬间隔和软间隔分类器是什么，以及其他等等等重要细节…………然而，Ng老师把这些都略去了，试图呈现给初学者最简单的一面，让读者花费最少的力气摸一下SVM的大门。
　　
　　这里一方面为Ng老师点赞，另一方面也要提醒各位读者，SVM其实不是你在Ng老师课程里看到的那么简单的……
　　
　　
　　

零-2、关于这篇博客

　　整理这篇关于SVM的博客时是比较棘手的，为什么为这么纠结，有两方面原因：
　　
　　1）因为Ng老师的SVM课程非常简单，讲解思路甚至跟常规的SVM教材都不一致（例如SVM是怎么来的），所以很难把Ng老师的讲解思路和常规SVM的讲解思路整合起来。
　　
　　2）SVM有着严密的数学理论，涉及的理论概念和数学公式一箩筐，深入浅出的文章已经不少，我再写一篇深入浅出的导论性质的博客，意义不大。如果后面时间和精力允许，我就把SVM相关的理论算法完完整整推导一遍。
　　
　　所以最后我觉得这篇博客还是只整理Ng老师在Coursera课程里的内容，同时做一定程度的扩展，如果读者在学习Ng课程时候有问题，可以在本博客里找找答案，如果读者想要深入学习SVM，建议找专业的资料研读（后面我会给一些）。
　　
　　
　　

零-3、SVM的优质博客和Tutorial等资料

　　网上已经有很多关于SVM的优质博客了，这里推荐几篇：
　　Jasper - SVM入门系列
　　http://www.blogjava.net/zhenandaci/category/31868.html
　　pluskid - 支持向量机系列
　　http://blog.pluskid.org/?page_id=683
　　JerryLead - 支持向量机系列
　　http://www.cnblogs.com/jerrylead/tag/Machine%20Learning/
　　
　　比较不错的Tutorial：
　　Microsoft - A Tutorial on Support Vector Machines for Pattern Recognition
　　https://www.microsoft.com/en-us/research/publication/a-tutorial-on-support-vector-machines-for-pattern-recognition/
　　Support Vector and Kernel Machines
　　http://www.support-vector.net/icml-tutorial.pdf
　　Support Vector Machine (and Statistical Learning Theory) Tutorial
　　http://www.cs.columbia.edu/~kathy/cs4701/documents/jason_svm_tutorial.pdf
　　
　　VC Dimension
　　http://www.svms.org/vc-dimension/

　　-
　　
　　

一、SVM的基本思想

1.1 常规Tutorial的讲解

　　SVM（Support Vector Mechines）的是一种定义在特征空间上的间隔最大的线性分类器。在李航的《统计学习方法中》，是这样描述SVM的基本思想：
　　支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
　　
　　也就是说，SVM不仅要求能将两类样本正确分开，而且要求几何间隔最大，因此我们很容易知道，SVM优化问题的解是唯一的。专业一点说法，SVM的学习算法是求解凸二次规划的最优化算法。
　　
　　基于上述思想，得到SVM的目标函数和约束条件，进而得到SVM的优化目标。
　　-
　　

1.2 Ng老师的讲解

　　再来看看Ng老师是怎么讲的。
　　Ng认为SVM是源自逻辑回归，是在逻辑回归的基础上，修改了样本代价计算函数、正则化参数等，原话是这样说的：
　　
　　很多监督学习算法都是从逻辑回归扩展出来的，比如神经网络，SVMs等，它们或多或少都与逻辑回归有那么些关系，甚至可以说，分类算法起源于逻辑回归，各种分类算法的差异主要在于代价函数计算、正则化参数等。
　　
　　基于上述思想，Ng推导出了SVM的优化目标。
　　
　　
　　
　　

二、优化目标（Optimization Objective）

2.1 常规Tutorial的讲解

　　在常规的SVM教材中，在讲解SVM的目标函数过程中，至少要涉及到数学概念：函数间隔和几何间隔。SVM被称作是大间隔分类器，这里的间隔指的就是几何间隔。
　　
　　有了这两个概念，通过SVM的基本思想就可以推导出SVM的目标函数和约束条件：
　　

　　
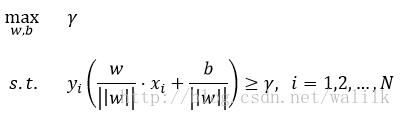
　　再利用函数间隔与几何间隔的关系式，将优化问题改写为：　　
　　
　　
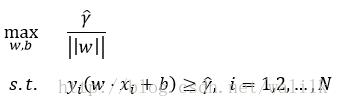
　　再利用max和min的等价关系，以及系数不影响优化问题的解，最终得到SVM的优化目标：
　　
　　
　　

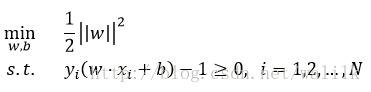
2.2 Ng老师的讲解

　　在Ng的课程里，SVM源自逻辑回归，那么首先看一下逻辑回归的代价函数，并逐步引出SVM的代价函数。
　　在逻辑回归中，对于单个样本 (x, y)，其代价函数为：
　　

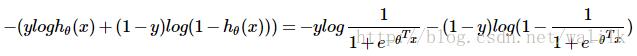
　　1）如果 y=1，令z=<θ, x>，则上述代价函数随z的变化曲线如下图：
　　
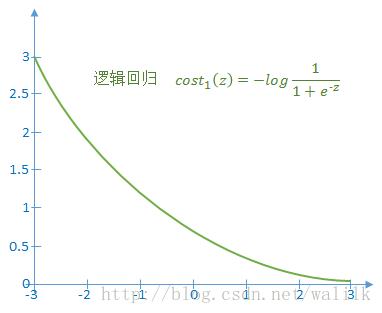
　　2）如果y=0，令z=<θ, x>，则上述代价函数随z的变化曲线如下图：
　　
　　
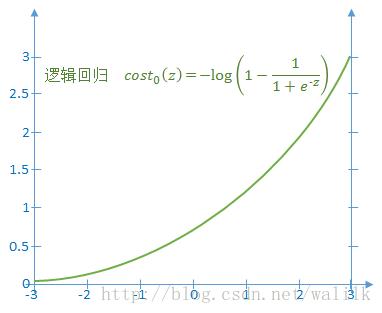
　　在SVM中，对于单个样本 (x, y)，将其代价函数改为：
　　
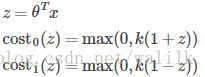
　　因此，
　　1）如果 y=1，令z=<θ, x>，则上述代价函数随z的变化曲线如下图：
　　
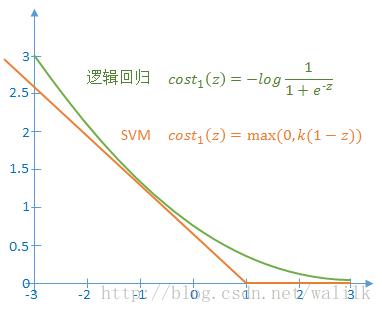
　　2）如果y=0，令z=<θ, x>，则上述代价函数随z的变化曲线如下图：
　　
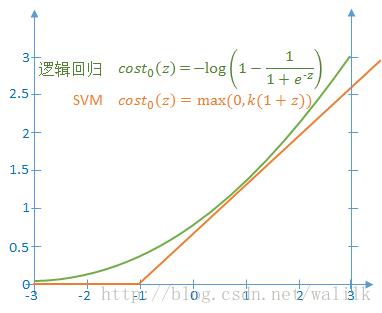
　　从图中可以看出，SVM使用一条折线作为新的代价函数。 新的代价函数形式可以带来计算上的优势，因为省去了 log(sigmoid(z)) 的计算，转而直接计算一个线性函数。
　　
　　综上对单个样本代价函数的对比分析，来对比逻辑回归和SVM的优化目标函数：
　　对于逻辑回归，其目标函数是：
　　
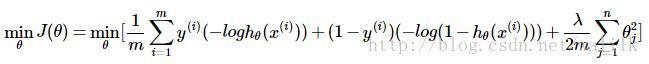
　　SVM在逻辑回归的基础上更换了目标函数中的样本代价计算，采用了更易于计算的分段线性函数，因此可以写为：
　　
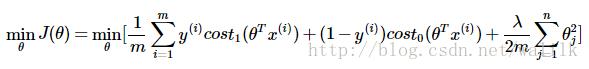
　　同时，SVM修改了正则化参数的形式（Ng老师说这仅仅是因为支持向量机的惯例……），用C代替1/λ，并去掉了系数中的1/m（不影响优化结果），得到SVM的目标函数如下。
　　
　　
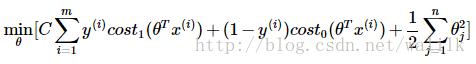
　　 Tip1：为何去掉1/m
　　目标函数乘以一个常数不影响最优解，例如最小化下面两个优化函数，其最优解是相同的：
　　
　　
　　
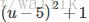
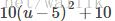
　　 Tip2：为何用C代替1/λ？
　　首先明确一点，用参数 C 替换 1/λ，这两个优化函数的参数解是一致的。
　　逻辑回归：A+λB
　　SVM：CA+B
　　
　　λ 和 C 都可以理解为目标函数优化过程中的控制参数（正则化参数），在优化过程中，权衡A和B的优化力度，也就是说利用 λ 和 C 来控制和影响优化过程。
　　
　　

2.3 C去哪里了

　　Ng这样讲解：
　　如果 C 非常大，则优化重点在于：选择参数使得第一项等于0，这就会导致新的优化问题，其最小化的目标函数的形式也发生改变，即：
　　

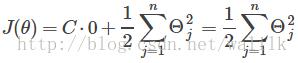
　　同时必须满足约束：
　　
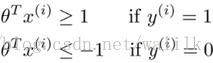
　　这两个约束条件用以保证 J(θ) 的第一项为0，换句话说，通过将 C 设置的非常大，从而将目标函数的最小化问题转换成一个：带约束的二次规划(quadratic programming, QP)问题，整体描述如下：
　　
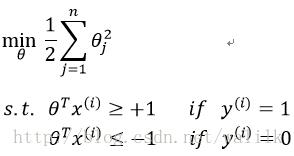
　　当求解这个二次规划问题的时候，会得到一个具有最大间隔性质的决策边界。
　　
　　以上是Ng老师对于SVM优化目标的推导过程，当时看这里着实不解，感觉不成体系。
　　就说这个C，大家发现没有，C没了……这TMD的就尴尬了……我们还要利用C来控制正则化程度呀…………
　　
　　

2.4 对比

　　李航《统计学习方法》中给出的SVM优化目标（未加正则项）：
　　

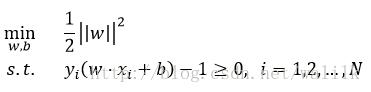
　　论文中大都也是这个形式，每一步推导由有理有据，非常好理解。
　　加上正则项，也就是SVM中的松弛变量，优化目标如下：
　　
　　
　　

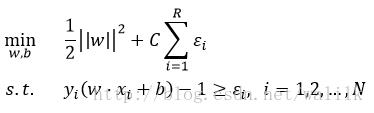
Ng老师给出的SVM优化目标：

　　
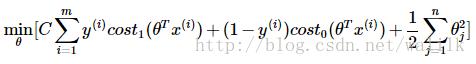
　　加上C非常大导致第一项为0，再加上约束条件，得到最终的SVM的优化问题：
　　
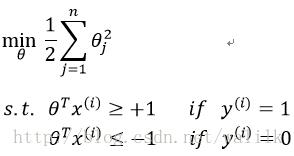
　　当时看到这个式子，真是令我百思不得其解也………………所以在这里我给出对比，希望同样有困惑的读者可以茅塞顿开。
　　
　　
　　

三、假设函数与决策边界（Hypothesis Function And Decision Boundary）

　　讨论SVM的假设函数也就是讨论给一个样本进来，SVM应该怎么输出。不同的Tutorial给出的观点不同，在不同的SVM开源实现中也是有差异的。
　　李航《统计学习方法》中给出的分类决策函数如下：
　　

　　
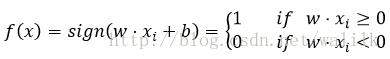
　　在有些Tutorial中，也可能会给出如下分类决策函数：
　　
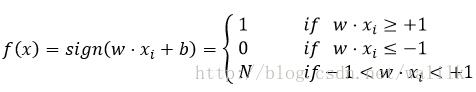
　　即处在间隔的的样本拒绝分类。
　　
　　两者的差别其实就是如何处在间隔中的样本，图示图下：
　　
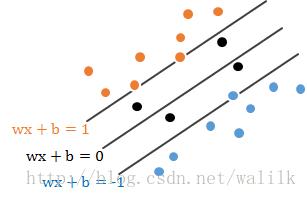
　　这个没有统一定论，而是要根据需求来选择。
　　
　　
　　

四、什么是支持向量

　　Ng的课程中并没有讲解什么是支持向量，这里给出简单介绍。
　　上图：
　　

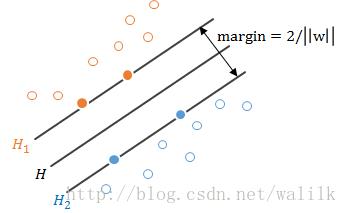
　　离H最近的正负样本刚好分别落在H1和H2上，这样的样本就是支持向量。
　　 可以看出，其实大部分样本对于分类超平面都没有作用，能决定分离超平面的只是训练样本中的很小一部分，也就是支持向量。
　　
　　
　　

五、核函数（Kernel Function）

　　核函数是SVM的精华，也是SVM处理分线性分类问题的关键。
　　核函数方法的基本思想是：
　　利用一个变换将原始特征映射到新的特征空间，通过在新特征空间学习线性分类模型，进而解决原始特征空间的非线性分类问题。
　　换句话说，核函数方法就是将原始特征空间线性不可分的问题，转换成一个新特征空间的线性可分问题来求解。
　　
　　Ng老师的课程中给出了核函数的的直观介绍，核函数在做的事情可以看作是特征映射：
　　

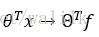
　　并给出了一种映射方式：
　　
　　
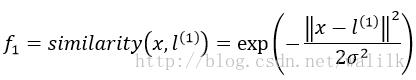
　　这也就是高斯核函数。
　　
　　Ng老师讲的很简单，更多关于核函数的原理，建议深入研读经典。
　　
　　
　　

六、最后的总结

　　SVM是个好东西，易于理解，易于使用，现在很多开源的SVM工具包都把SVM算法封装的极好，拿着教程就可以分分钟搞定简单的分类问题。但同时，SVM涉及的问题也是非常多的，可研究的点也是很丰富，我们课题组也有同学在博士期间一直研究SVM，所以大家可不要小瞧了SVM这个神器。

　　通常在拿到一个机器学习问题时候我会拿SVM先试一试，这样可以大致评估一下问题的难度，并可以及时发现任务的难点在哪里。
　　
　　对于Ng所讲的SVM，是比较简单的版本，掌握了课程的内容，基本就可以在任务中使用SVM了，比如libsvm等。但想要深入理解这个神器，还是得找本教材好好研究一下才可以。