CS231n笔记3--Gradient Descent与Backward Propagation
Posted LiemZuvon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CS231n笔记3--Gradient Descent与Backward Propagation相关的知识,希望对你有一定的参考价值。
Gradient Descent与Backward Propagation
梯度下降-Gradient Descent
求梯度的方法
- 根据梯度的定义:Numerical Method
- 利用求导的常用公式
根据梯度的定义求梯度
f′(x)=limΔx→0f(x+Δx)−f(x)Δx
根据上面的式子,我们可以用一个非常小的 Δx 来近似求导。
优点:
- 实现简单
- 代码直观
- 常用作梯度检测
缺点:
- 计算量大
- 不稳定
计算量大:因为每对一个参数求梯度,就需要一次正向的计算,根据正向计算的复杂度增大,梯度的计算量也会相应的增大,放在深度学习这种庞大的模型中会导致计算效率低下
不稳定:由于这种方法只是一种近似的方法,效果取决于选取的 Δx 的大小,当 Δx 太大时,不具代表性,当 Δx 太小时,很有可能会因为计算机的精度问题而导致原本应该很大的梯度最后变成零
下面给出python代码实现:
def gradcheck_naive(f, x):
"""
Gradient check for a function f
- f should be a function that takes a single argument and outputs the cost and its gradients
- x is the point (numpy array) to check the gradient at
"""
rndstate = random.getstate()
random.setstate(rndstate)
fx, grad = f(x) # Evaluate function value at original point
h = 1e-4
# Iterate over all indexes in x
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
ix = it.multi_index
# replace with return to avoid side effects
x[ix] += h # increment by h
random.setstate(rndstate)
fxh, _ = f(x) # evalute f(x + h)
x[ix] -= 2 * h # restore to previous value (very important!)
random.setstate(rndstate)
fxnh, _ = f(x)
x[ix] += h
numgrad = (fxh - fxnh) / 2 / h
# Compare gradients
reldiff = abs(numgrad - grad[ix]) / max(1, abs(numgrad), abs(grad[ix]))
if reldiff > 1e-5:
print "Gradient check failed."
print "First gradient error found at index %s" % str(ix)
print "Your gradient: %f \\t Numerical gradient: %f" % (grad[ix], numgrad)
return
it.iternext() # Step to next dimension
print "Gradient check passed!"
利用求导的常见公式
求导常见公式:
http://baike.baidu.com/link?url=QTF45fRpmnGVcbsni2AqQB-XpqSQtFNOmeT80ti7vIQ9EV8eYjGYamCazte-VKAW
我们这里更关注的是求导的链式法则
例如 ,使用链式法则对y求导可得:
利用链式法则和常见的求导公式,我们已经可以解决在深度学习中遇到的所有求梯度的问题了,下面我们来讲讲在后向传播算法Backward Propagation中,链式法则和常见的求导公式是怎么派上用场的。
后向传播算法-Backward Propagation
小试牛刀
我们先看一个简单的例子
求f对其输入x,y,z的梯度。
为了方便理解我们可以先画出其对应的计算流程图,如下
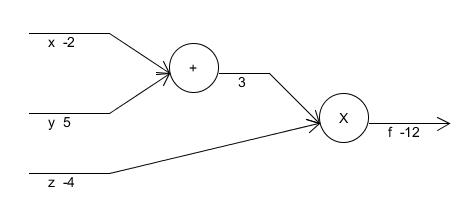
为了求x处的梯度,我们可以求在运算+处的梯度,然后利用该梯度乘于运算+对x的梯度(这里是为了能够与图对应才说运算+出的梯度,而非正规的数学形式,读者不要被我误导了)
这时我们发现我们需要求f对运算+处的梯度,就要用到运算*对运算+的梯度
而注意到f即是运算*的结果,因此 ,整合一下,我们可以得到下列的求梯度步骤:
仔细观察上面的求导步骤,我们可以看出,为了求x处的导数,我们从最后面的结果开始,往前求导,并不断的累乘,得到了最后的结果,这个就是Backward Propagation的原理,就是这么简单,剩下的y,z我希望读者能够自己试着求下,最后的结果应该是。
来点狠的
下面我们将根据上面的步骤,来看看一个稍微复杂一点的情况我们应该怎么利用BP。我们用CS231课上的例子来演示,读者们可以拿出纸笔跟着计算一下。
给出Sigmoid式子:
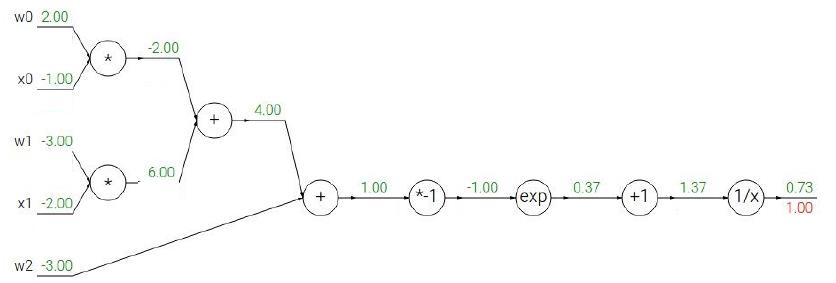
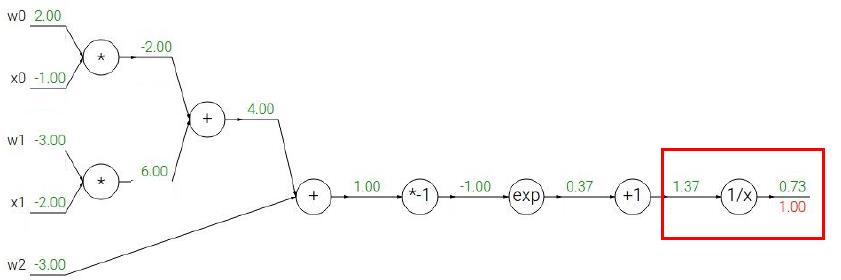
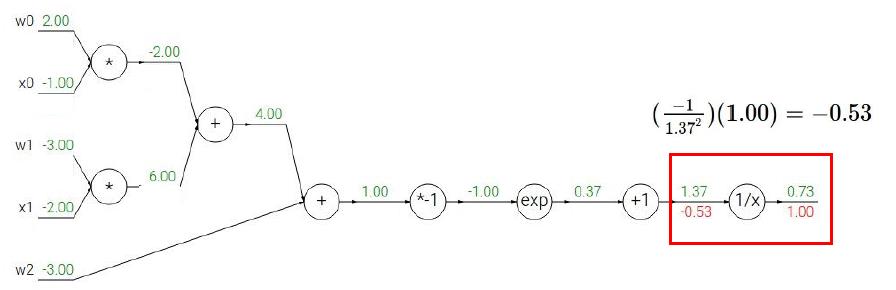
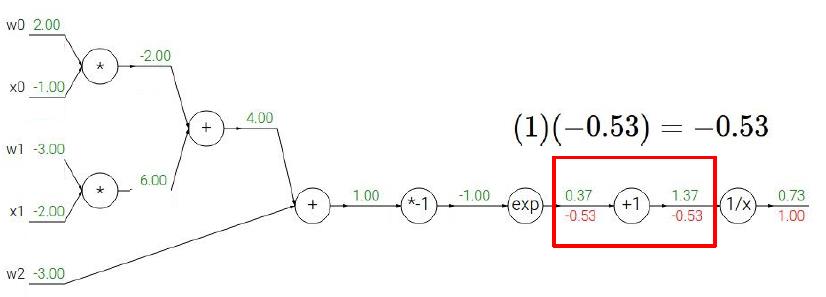
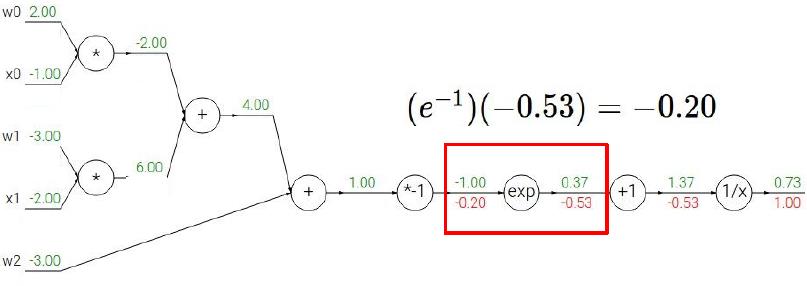

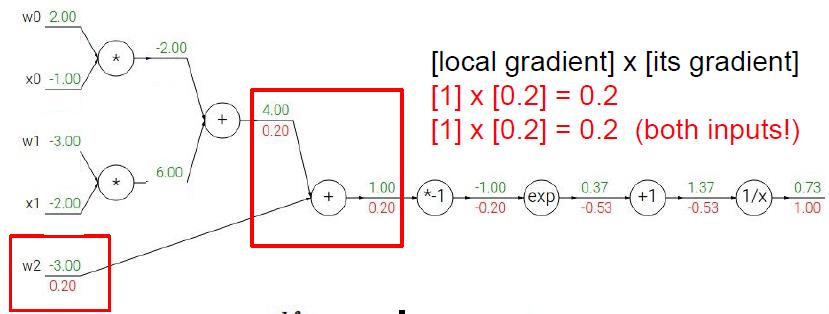
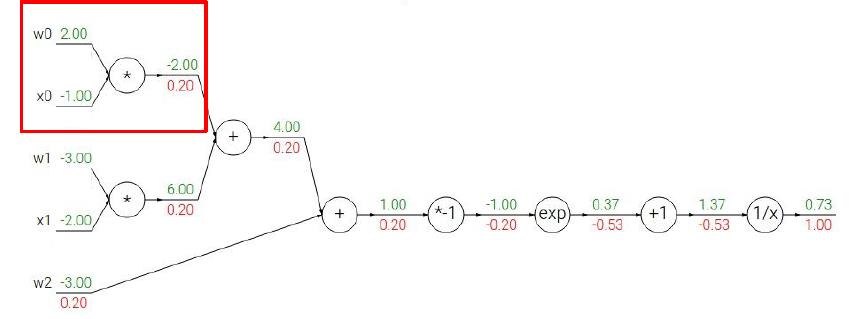
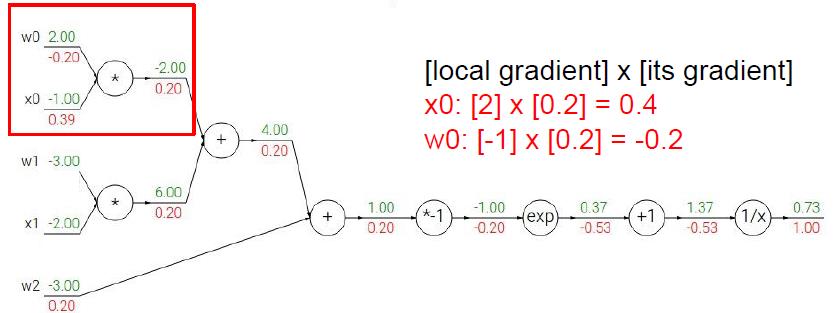
相信上面的步骤读者看得都很直观,所以我也就不多赘述了,最后补充一点,当遇到计算图出现下面情形时
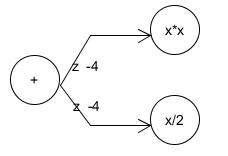
为了求运算+处的梯度,我们需要分别求运算xx对运算+的导数以及运算x/2对运算+的导数,并将这两个导数相加即可!例如,对于上图运算+处的导数应该是2z+0.5=-7.5
后言
到这里,我们已经具备了求解所有深度学习导数的能力,在后面的环节中,我们会进入深度学习的层的学习,并利用本章学习的知识,给出每一层的计算以及梯度的求解!
以上是关于CS231n笔记3--Gradient Descent与Backward Propagation的主要内容,如果未能解决你的问题,请参考以下文章