Opencv2.4.9源码分析——Neural Networks
Posted zhaocj
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Opencv2.4.9源码分析——Neural Networks相关的知识,希望对你有一定的参考价值。
一、原理
神经网络(Neural Networks)是一种模仿生物神经系统的机器学习算法。该算法的提出最早可追述至上个世纪四十年代,这几乎与电子计算机的历史同步。但它的发展并非一帆风顺,也经历了初创阶段—黄金阶段—停滞阶段—复兴阶段,直到目前的高速发展阶段。年初由Google公司开发的神经网络围棋——AlphaGo击败世界围棋冠军李世石,使神经网络技术更是受到世人的注目,因为它的意义要远大于1997年IBM的超级计算机——深蓝击败国际象棋大师卡斯帕罗夫。
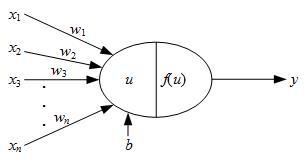
图1 神经元
与生物神经系统相似,人工神经网络也是由若干个神经元构成。如图1所示,x1、x2、…xn为该神经元的输入,y为该神经元的输出。显然,不同的输入对神经元的作用是不同的,因此用权值w1、w2、…wn来表示这种影响程度的不同。神经元内部包括两个部分,第一个部分是对输入的加权求和,第二个部分是对求和的结果进行“激活”,得到输出。加权求和的公式为:
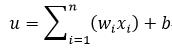 (1)
(1)
式中,b为偏移量,该偏移量也可以定义为输入恒为1的权值w0,即权值也包括偏移量,因此式1可以改写为:
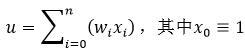 (2)
(2)
激活的公式为:
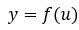 (3)
(3)
式中,f(·)称为激活函数。激活函数可以有多种形式,如线性函数:
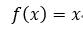 (4)
(4)
阈值函数:
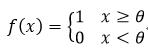 (5)
(5)
Sigmoid函数:
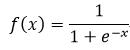 (6)
(6)
对称Sigmoid函数:
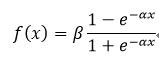 (7)
(7)
双曲正切函数:
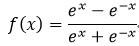 (8)
(8)
高斯函数:
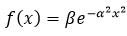 (9)
(9)
式7和式9中的α和β均为函数的系数。
前馈神经网络是神经网络的一种,也是最常用的一种神经网络。它包括一个输入层,一个输出层和若干个隐含层,因此具有该种拓扑结构的神经网络又称为多层感知器(MLP)。如图2所示,该MLP包括一个输入层,一个输出层和一个隐含层,其中某一层的神经元只能通过一个方向连接到下一层的神经元。
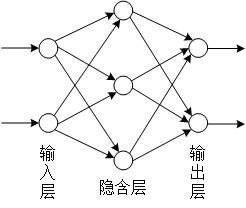
图2 前馈神经网络
对于MLP,我们可以用Backprop(backward propagation oferrors,误差的反向传播,简称BP)算法实现它的建模,该算法具有结构简单、易于实现等特点。
Backprop算法是一种监督的机器学习算法,输入层的神经元数量一般为样本的特征属性的数量,输出层的神经元的数量一般为样本的所有的可能目标值的数量,如果是分类问题,则为样本的分类数量,因此,与其他机器学习算法不同,在MLP中,样本对应的响应值应该是一个相量,相量的维数与输出层的神经元的数量一致。而隐含层的层数以及各层神经元的数量则根据实际情况进行选取。Backprop算法的核心思想是:通过前向通路(箭头的方向)得到误差,再把该误差反向传播实现权值w的修正。
MLP的误差可以用平方误差函数来进行表示。设某个样本x对应的目标值为t,样本x有n个特征属性,即x=x1, x2,…,xn,目标值t有J种可能的值,即t=t1, t2,…,tJ,因此该MLP的输入层(即第一层)一共有n个神经元,输出层(即第L层,设MLP一共有L层)一共有J个神经元。设样本x经过前向通路得到的最终输出为y=y1L,y2L,…,yJL ,输出y的下标表示y所在层的神经元索引,上标表示y所在的层,则该样本的平方误差为:
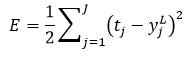 (10)
(10)
之所以式10中的平方误差函数要除以2,是为了便于后面的求导运算,因为它并不影响误差的变化趋势。
显然,MLP算法的目标就是使E最小。由图1可知,式10中的yjL是由上一层(即第L-1层)所有神经元的输出经加权激活后得到,而第L-1层神经元的输出又由第L-2层的所有神经元的输出经加权激活后得到,因此可以说误差E是全体权值w的函数,通过改变权值w,就可达到使误差E最小的目的。
Backprop算法是一种迭代的方法,也就是我们不必通过一次改变权值w来达到使E最小的目的,我们只需渐进的减小E即可。w和E的关系可以形象的比作山坡,山的高度是误差,平面的维度空间是权值,山坡越陡(误差大),平面维度空间的变化(权值的变化)就越大,权值的变化与误差有关,而当权值改变时,误差就要重新计算。这样两者相互作用,即不断迭代,直到误差小于某个值(即收敛)为止。该方法就是我们常用的梯度下降法。
误差E对权值w的导数为w的变化率,即:
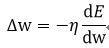 (11)
(11)
式中,η表示学习效率,它的取值在0和1之间,它起到控制收敛速度和准确性的作用。如果η过大,导致振荡,则很难收敛,如果η过小,则需要更长的时间收敛。为了改变因η选取的不好而带来的问题,又引入了被称为“动量(momentum)”的参数μ,则w的变化率改写为:
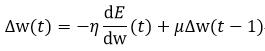 (12)
(12)
式中,t表示当前,t-1表示上一次,而t+1表示下一次,因此本次的w变化率不仅与E的导数有关,还与上次w的变化率有关。参数μ的作用是提供了一些惯性,使之平滑权值的随机波动。由Δw更新当前的权值w,即:
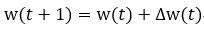 (13)
(13)
式13所表示的更新权值的过程是从输出层经过隐含层,向输入层逐层推进的过程,也就是误差反向传播的过程,这也就是Backprop算法名称的由来。当所有的权值更新完后,再由前向通路计算得到误差E,此时就完成了一次迭代。
下面我们就来讲解如何由前向通路得到误差E,又如何计算w的变化率,及由反向通路更新w的过程。
设wkhl表示第l层的第k个神经元与第l-1层的第h个神经元之间连接时的权值。由式1和式3可以,第l层的第k个神经元的输出ykl为:
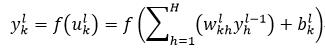 (14)
(14)
式中,ukl表示第l层的第k个神经元的加权和,bkl表示第l层的第k个神经元的偏移量,即
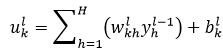 (15)
(15)
这里我们设第l层一共有K个神经元,第l-1层一共有H个神经元。则第l层的所有K个神经元的加权和ul可以比较方便的用矩阵的形式表示:
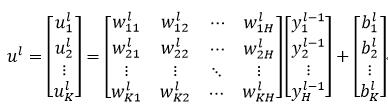 (16)
(16)
则第l层的所有K个神经元输出yl为:
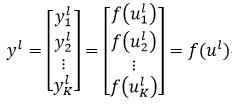 (17)
(17)
我们把每层的输出yl级联在一起,就构成了MLP的前向通路,则当一个样本x添加到MLP的输入层时,经过层层计算,最终得到了MLP的输出yL,把yL带入到式10,就得到了该样本x的误差。
前向通路的计算过程总结为:样本经过权值的计算后,再经过激活函数得到输出,最终得到误差,即
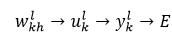 (18)
(18)
下面我们计算权值的变化率,即对误差求导。由链式法则可知,样本x的误差E对权值wkhl的偏导数可以表示为:
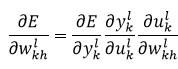 (19)
(19)
由上式可知,要想得到误差的导数,只需要计算等式右侧的三个偏导即可。上式中右侧的前两个偏导又可以定义为δkl,即
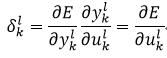 (20)
(20)
由式1可以得到式19右侧的第三个偏导:
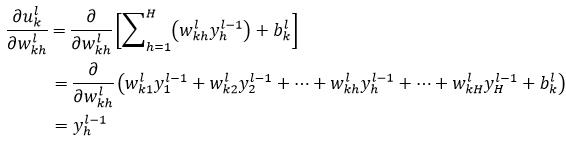 (21)
(21)
式21表示求导的结果为第l-1层的第h个神经元的输出,如果第l-1层为输入层,则yhl-1为样本的第h个特征属性值xh。
式19右侧的第二个偏导为:
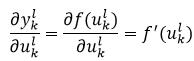 (22)
(22)
式22中的f(·)就是式4至式9给出的激活函数。式4所表示的函数的导数为:
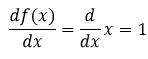 (23)
(23)
式6所表示的函数的导数为:
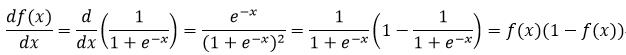 (24)
(24)
式7所表示的函数的导数为:
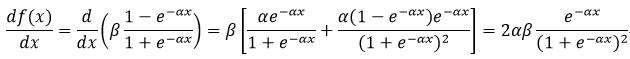 (25)
(25)
式8所表示的函数的导数为:
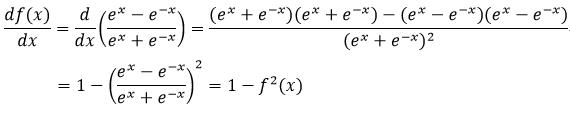 (26)
(26)
式9所表示的函数的导数为:
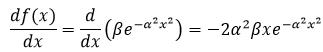 (27)
(27)
下面计算式19右侧的第一个偏导。当ykl为输出层的输出时,即yjL,该项的偏导很简单:
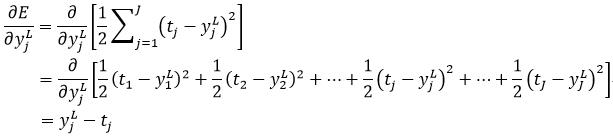 (28)
(28)
因此,基于输出层的权值wjhL的误差导数,即式19为:
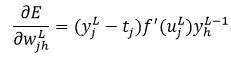 (29)
(29)
其中,
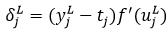 (30)
(30)
而当ykl为MLP内部神经元的输出时,要想计算式19右侧的第一个偏导就略显复杂。这是因为我们不知道内部神经元的输出误差,而我们只知道输出层的误差,所以我们需要把内部神经元误差传递到输出层。很显然,所有接受到前面神经元输出的后续神经元都会受到该神经元误差的影响,而后续的神经元都直接或间接的与前面神经元连接,因此内部所有神经元的误差最终都会传递到输出层的所有神经元上。
设yhl为中间第l层的第h个神经元的输出,则
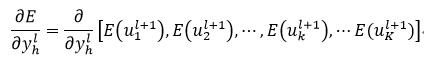 (31)
(31)
式中,E(ukl+1)表示误差E是ukl+1的函数。式31表明,第l层的第h个神经元的输出误差传递到了第l+1层内的所有K个神经元内,则
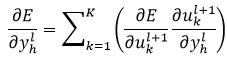 (32)
(32)
由式15可以得到式32中右侧第二个偏导为:
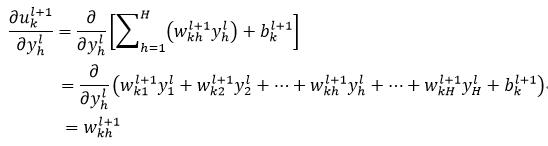 (33)
(33)
由式20可以得到式32中右侧第一个偏导
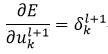 (34)
(34)
因此,基于中间层的权值wkhl的误差导数,即式19为:
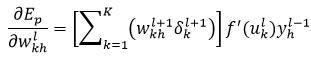 (35)
(35)
因为我们是通过反向传播的方式计算式19,即先得到最后层(即输出层)的结果,再计算倒数第二层,以此类推,所以在计算第l层误差导数时,事先一定会得到第l+1层的δkl+1,从而保证式35能够顺利计算。现在我们把式29和式35写在一起,完整的得到误差导数:
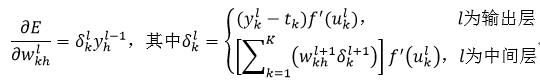 (36)
(36)
由式36就得到了基于wkhl的误差导数,再把该结果带入式11或式12中就得到了该权值的变化率,最后由式13就得到了更新后的权值。在反向传播的过程中,所有权值都经过了上述计算后,就得了更新后的所有权值。用新得到的权值计算下一个样本,以此类推,直至所有样本都经过MLP计算为止,此时就完成了所有样本的一次迭代过程。在每次迭代完成后,我们可以比较两次迭代的误差大小,如果两个误差之差满足我们的设计要求,则可以终止迭代,否则继续下次迭代。该方法也称作在线方法,因为样本是一个一个的进入MLP,每完成一个样本的计算就更新一次权值。为了增加鲁棒性,在每次迭代之前,可以把全体样本打乱顺序,这样每次迭代的过程中提取样本的顺序就会不相同。除了在线方法,还有一种方法称为批量方法,即把所有样本的误差累加在一起,用该累加误差计算误差的导数,进而得到权值的变化率。
在完成上述计算的过程之前,首先要解决的问题就是初始化权值,即第一次权值如何选择。一般的做法是随机选择很小的值作为初始权值,但这样做收敛较慢。比较好的方法是采用Nguyen-Widrow算法初始化权值。它的基本思想是每个神经元都有属于自己的一个区间范围,通过初始化权值就可以限制它的区间位置,当改变权值时,该神经元也只是在自己的区间范围内变化,因此该方法可以大大提高收敛速度。
Nguyen-Widrow算法初始化MLP权值的方法为:对于所有连接输出层的权值和偏移量,初始值为一个在正负1之间的随机数。对于中间层的权值,初始为:
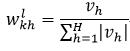 (37)
(37)
式中,vh是一个在正负1之间的随机数,H为第l-1层神经元的数量。而中间层的偏移量初始为:
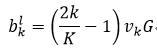 (38)
(38)
式中,vk是一个在正负1之间的随机数,K为第l层神经元的数量,而G为:
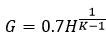 (39)
(39)
以上我们介绍了经典的Backprop算法,该算法还是有一些不足之处。首先是它的学习效率η是需要我们事先确定好;另外权值的变化是基于误差梯度的变化率,虽然这点乍一看,似乎没有问题,但我们不敢保证它永远正确有效。为此Riedmiller等人提出了RPROP算法(resilient backpropagation),用以改善Backprop算法。
RPROP算法的权值变化率并不是基于误差梯度的变化率,而是基于它的符号:
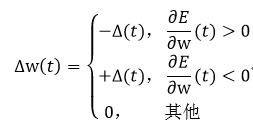 (40)
(40)
式中,Δ(t)为:
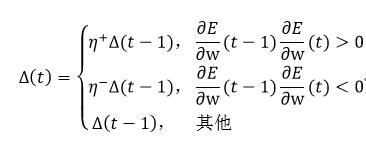 (41)
(41)
式中,常数η+必须大于1,常数η-必须在0和1之间。式40和式41中的∂E/∂w由式36得到。
关于式40和式41,还有一些问题需要解决,那就是Δ(t)的初始值和它的变化范围。Riedmiller等人已经给出了Δ(0)初始化为0.1是比较正确的选择,而Δmax(t)=50,Δmin(t)=10-6可以有效的防止溢出。
二、源码分析
Opencv的神经网络实现了MLP算法,具体为BACKPROP算法和RPROP算法两种,BACKPROP算法使用的是在线方法,RPROP算法使用的是批量方法。
结构CvANN_MLP_TrainParams表示MLP训练算法所需的参数,它的构造函数为:
CvANN_MLP_TrainParams::CvANN_MLP_TrainParams()
//表示训练迭代的终止条件,默认为迭代次数(大于1000)和权值变化率(小于0.01)
term_crit = cvTermCriteria( CV_TERMCRIT_ITER + CV_TERMCRIT_EPS, 1000, 0.01 );
//具体应用的MLP算法,默认为RPROP
train_method = RPROP;
// bp_dw_scale为式13中的η,bp_moment_scale为式13中的μ
bp_dw_scale = bp_moment_scale = 0.1;
//RPROP算法所需的参数(式40和式41),依次为Δ(0)、η+、η-、Δmin(t)、Δmax(t)
rp_dw0 = 0.1; rp_dw_plus = 1.2; rp_dw_minus = 0.5;
rp_dw_min = FLT_EPSILON; rp_dw_max = 50.;
CvANN_MLP_TrainParams::CvANN_MLP_TrainParams( CvTermCriteria _term_crit,
int _train_method,
double _param1, double _param2 )
term_crit = _term_crit;
train_method = _train_method;
bp_dw_scale = bp_moment_scale = 0.1;
rp_dw0 = 1.; rp_dw_plus = 1.2; rp_dw_minus = 0.5;
rp_dw_min = FLT_EPSILON; rp_dw_max = 50.;
if( train_method == RPROP ) //RPROP算法
rp_dw0 = _param1; //输入参数_param1表示Δ(0)
if( rp_dw0 < FLT_EPSILON ) //Δ(0)不能太小
rp_dw0 = 1.;
rp_dw_min = _param2; //输入参数_param2表示Δmin(t)
rp_dw_min = MAX( rp_dw_min, 0 ); //Δmin(t)不能小于0
else if( train_method == BACKPROP ) //BACKPROP算法
bp_dw_scale = _param1; //输入参数_param1表示η
//确保η在一个合理的范围内
if( bp_dw_scale <= 0 )
bp_dw_scale = 0.1;
bp_dw_scale = MAX( bp_dw_scale, 1e-3 );
bp_dw_scale = MIN( bp_dw_scale, 1 );
bp_moment_scale = _param2; //输入参数_param2表示μ
//确保μ在一个合理的范围内
if( bp_moment_scale < 0 )
bp_moment_scale = 0.1;
bp_moment_scale = MIN( bp_moment_scale, 1 );
//如果输入参数_train_method为除了RPROP和BACKPROP以外的值,则程序给出的算法为RPROP
else
train_method = RPROP;
类CvANN_MLP实现了MLP模型,不像其他的机器学习模型,MLP模型的构建和训练是由两个不同步骤来完成的。我们先给出CvANN_MLP类的一个构造函数:
CvANN_MLP::CvANN_MLP( const CvMat* _layer_sizes,
int _activ_func,
double _f_param1, double _f_param2 )
//_layer_sizes用整型相量的形式表示MLP中的一共有几层(包括一个输入层,一个输出层,以及若干个隐含层),每层有多少个神经元,相量的维数表示层数,相量元素的值表示对应层的神经元的数量
//_activ_func表示激活函数的类型,可以为CvANN_MLP::IDENTITY,CvANN_MLP::SIGMOID_SYM或CvANN_MLP::GAUSSIAN,分别表示线性激活函数(式4),对称SIGMOID激活函数(式7),和高斯激活函数(式9),对于所有的神经元,都需采用同一个激活函数
//_f_param1和_f_param2分别表示激活函数中的参数α和β
//layer_sizes与输入参数_layer_sizes的含义相同,wbuf表示存储权值的空间
layer_sizes = wbuf = 0;
//输出层规范化用到的一些变量
min_val = max_val = min_val1 = max_val1 = 0.;
weights = 0; //用来表示权值
rng = &cv::theRNG(); //表示随机数
default_model_name = "my_nn";
//调用create函数,构建MLP模型,该函数在下面给出详细介绍
create( _layer_sizes, _activ_func, _f_param1, _f_param2 );
构建MLP模型:
void CvANN_MLP::create( const CvMat* _layer_sizes, int _activ_func,
double _f_param1, double _f_param2 )
CV_FUNCNAME( "CvANN_MLP::create" );
__BEGIN__;
// l_count表示MLP的层数,buf_sz表示开辟存储权值的内存空间的大小
int i, l_step, l_count, buf_sz = 0;
int *l_src, *l_dst;
clear(); //清除和初始化一些全局变量
//判断_layer_sizes的格式、数据类型是否正确,_layer_sizes必须是相量形式,数据类型必须为CV_32SC1,不对则报错
if( !CV_IS_MAT(_layer_sizes) ||
(_layer_sizes->cols != 1 && _layer_sizes->rows != 1) ||
CV_MAT_TYPE(_layer_sizes->type) != CV_32SC1 )
CV_ERROR( CV_StsBadArg,
"The array of layer neuron counters must be an integer vector" );
//调用set_activ_func函数,设置激活函数,该函数在后面给出详细介绍
CV_CALL( set_activ_func( _activ_func, _f_param1, _f_param2 ));
//l_count为相量_layer_sizes的维数,即MLP的层数L
l_count = _layer_sizes->rows + _layer_sizes->cols - 1;
l_src = _layer_sizes->data.i; //_layer_sizes的首地址指针
//_layer_sizes元素的步长
l_step = CV_IS_MAT_CONT(_layer_sizes->type) ? 1 :
_layer_sizes->step / sizeof(l_src[0]);
//创建相量layer_sizes
CV_CALL( layer_sizes = cvCreateMat( 1, l_count, CV_32SC1 ));
l_dst = layer_sizes->data.i; //layer_sizes的首地址指针
max_count = 0; //表示某层中,最多的神经元的数量
for( i = 0; i < l_count; i++ ) //遍历MLP的所有层
int n = l_src[i*l_step]; //得到当前层的神经元的数量
//满足条件:0 < i && i < l_count-1,说明i为隐含层,该if语句的作用是,如果是隐含层,则神经元的数量一定要大于1,如果是输入层或输出层,则神经元的数量至少应为1,否则程序报错
if( n < 1 + (0 < i && i < l_count-1))
CV_ERROR( CV_StsOutOfRange,
"there should be at least one input and one output "
"and every hidden layer must have more than 1 neuron" );
//把当前层的神经元的数量赋值给变量layer_sizes所对应的层
l_dst[i] = n;
//记录下MLP层中数量最多的神经元的数量
max_count = MAX( max_count, n );
//统计该MLP一共有多少个权值,其中也包括偏移量
if( i > 0 )
buf_sz += (l_dst[i-1]+1)*n;
// l_dst[0]表示输入层神经元的数量,l_dst[l_count-1]表示输出层神经元的数量
buf_sz += (l_dst[0] + l_dst[l_count-1]*2)*2;
//创建相量wbuf,用于存储权值
CV_CALL( wbuf = cvCreateMat( 1, buf_sz, CV_64F ));
//为weights开辟内存空间
CV_CALL( weights = (double**)cvAlloc( (l_count+2)*sizeof(weights[0]) ));
//weights[0]指向wbuf的首地址,它表示输入层规范化所用的系数
weights[0] = wbuf->data.db;
//定义weights[1]首地址
weights[1] = weights[0] + l_dst[0]*2;
// weights[1]至weights[l_count]表示MLP相应层的所有权值,包括偏移量(即公式中的+ 1),它存放在数组的最后一个位置上
for( i = 1; i < l_count; i++ )
weights[i+1] = weights[i] + (l_dst[i-1] + 1)*l_dst[i];
// weights[l_count]和weights[l_count+1]都表示输出层规范化所用到的系数,训练时用的是weights[l_count+1]内的值,预测时用的是weights[l_count]内的值
weights[l_count+1] = weights[l_count] + l_dst[l_count-1]*2;
__END__;
设置激活函数:
void CvANN_MLP::set_activ_func( int _activ_func, double _f_param1, double _f_param2 )
CV_FUNCNAME( "CvANN_MLP::set_activ_func" );
__BEGIN__;
//判断激活函数是否为线性、对称SIGMOR、或高斯中的一种
if( _activ_func < 0 || _activ_func > GAUSSIAN )
CV_ERROR( CV_StsOutOfRange, "Unknown activation function" );
activ_func = _activ_func; //赋值
//根据不同的激活函数类型,赋予不同的参数
switch( activ_func )
case SIGMOID_SYM: //对称SIGMOID激活函数
max_val = 0.95; min_val = -max_val;
max_val1 = 0.98; min_val1 = -max_val1;
//如果用户定义的对称SIGMOID激活函数的参数过小,则重新赋值
if( fabs(_f_param1) < FLT_EPSILON )
_f_param1 = 2./3;
if( fabs(_f_param2) < FLT_EPSILON )
_f_param2 = 1.7159;
break;
case GAUSSIAN: //高斯激活函数
max_val = 1.; min_val = 0.05;
max_val1 = 1.; min_val1 = 0.02;
//如果用户定义的高斯激活函数的参数过小,则重新赋值
if( fabs(_f_param1) < FLT_EPSILON )
_f_param1 = 1.;
if( fabs(_f_param2) < FLT_EPSILON )
_f_param2 = 1.;
break;
default: //线性激活函数
min_val = max_val = min_val1 = max_val1 = 0.;
_f_param1 = 1.;
_f_param2 = 0.;
f_param1 = _f_param1; //赋值α
f_param2 = _f_param2; //赋值β
__END__;
int CvANN_MLP::train( const CvMat* _inputs, const CvMat* _outputs,
const CvMat* _sample_weights, const CvMat* _sample_idx,
CvANN_MLP_TrainParams _params, int flags )
//_inputs表示MLP的输入数据,即待训练的样本数据
//_outputs表示MLP的输出数据,即待训练的样本响应值或分类标签
//_sample_weights表示事先定义好的样本的权值
//_sample_idx表示真正被用于训练的样本数据的索引,即有一部分样本不用于训练MLP
//_params表示MLP模型参数
//flags表示控制算法的参数,可以为UPDATE_WEIGHTS、NO_INPUT_SCALE和NO_OUTPUT_SCALE,以及它们的组合,这些变量的含义为:UPDATE_WEIGHTS表示算法需要更新网络的权值;NO_INPUT_SCALE表示算法无需规范化MLP的输入数据,规范化的意思就是使输入样本的特征属性均值为0,标准方差为1;NO_OUTPUT_SCALE表示算法无需归一化MLP的输出数据
//该函数返回迭代次数
const int MAX_ITER = 1000; //表示最大迭代次数
const double DEFAULT_EPSILON = FLT_EPSILON; //定义一个常数
double* sw = 0; //表示样本的权值
CvVectors x0, u; //分别表示MLP的输入数据和输出数据
int iter = -1; //表示训练MLP所需的迭代次数
//初始化首地址指针
x0.data.ptr = u.data.ptr = 0;
CV_FUNCNAME( "CvANN_MLP::train" );
__BEGIN__;
int max_iter;
double epsilon;
params = _params; //MLP模型参数
// initialize training data
//调用prepare_to_train函数,为MLP模型的训练准备参数,该函数在后面给出详细的介绍
CV_CALL( prepare_to_train( _inputs, _outputs, _sample_weights,
_sample_idx, &x0, &u, &sw, flags ));
// ... and link weights
//如果没有定义UPDATE_WEIGHTS,则需要调用init_weights函数进行权值的初始化,该函数在后面给出了详细的介绍
if( !(flags & UPDATE_WEIGHTS) )
init_weights();
//得到最大迭代次数
max_iter = params.term_crit.type & CV_TERMCRIT_ITER ? params.term_crit.max_iter : MAX_ITER;
max_iter = MAX( max_iter, 1 ); //最大迭代次数必须大于等于1
//得到用前后两次误差之差来判断终止迭代的系数
epsilon = params.term_crit.type & CV_TERMCRIT_EPS ? params.term_crit.epsilon : DEFAULT_EPSILON;
epsilon = MAX(epsilon, DBL_EPSILON);
//重新定义终止MLP训练的条件
params.term_crit.type = CV_TERMCRIT_ITER + CV_TERMCRIT_EPS;
params.term_crit.max_iter = max_iter;
params.term_crit.epsilon = epsilon;
//如果是BACKPROP算法,则调用train_backprop函数,如果是RPROP算法,则调用train_rprop函数,这个两个函数在后面有详细的介绍
if( params.train_method == CvANN_MLP_TrainParams::BACKPROP )
CV_CALL( iter = train_backprop( x0, u, sw ));
else
CV_CALL( iter = train_rprop( x0, u, sw ));
__END__;
//释放内存空间
cvFree( &x0.data.ptr );
cvFree( &u.data.ptr );
cvFree( &sw );
return iter; //返回迭代次数
为训练MLP模型准备参数:
bool CvANN_MLP::prepare_to_train( const CvMat* _inputs, const CvMat* _outputs,
const CvMat* _sample_weights, const CvMat* _sample_idx,
CvVectors* _ivecs, CvVectors* _ovecs, double** _sw, int _flags )
bool ok = false; //该函数正确返回的标识
CvMat* sample_idx = 0; //表示样本数据的索引
CvVectors ivecs, ovecs; //分别表示输入层和输出层的数据
double* sw = 0; //表示样本的权值
int count = 0;
CV_FUNCNAME( "CvANN_MLP::prepare_to_train" );
ivecs.data.ptr = ovecs.data.ptr = 0; //初始化为0
assert( _ivecs && _ovecs ); //确保输入参数_ivecs和_ovecs有效
__BEGIN__;
const int* sidx = 0; //该指针指向sample_idx
// sw_type和sw_count分别表示样本权值数据的类型和数量
int i, sw_type = 0, sw_count = 0;
int sw_step = 0; //示样本权值数据的步长
double sw_sum = 0; //表示样本权值的累加和
//通过判断layer_sizes是否被正确赋值,来确保MLP模型是否被构建好
if( !layer_sizes )
CV_ERROR( CV_StsError,
"The network has not been created. Use method create or the appropriate constructor" );
//判断输入参数_inputs是否正确
if( !CV_IS_MAT(_inputs) || (CV_MAT_TYPE(_inputs->type) != CV_32FC1 &&
CV_MAT_TYPE(_inputs->type) != CV_64FC1) || _inputs->cols != layer_sizes->data.i[0] )
CV_ERROR( CV_StsBadArg,
"input training data should be a floating-point matrix with"
"the number of rows equal to the number of training samples and "
"the number of columns equal to the size of 0-th (input) layer" );
//判断输入参数_outputs是否正确
if( !CV_IS_MAT(_outputs) || (CV_MAT_TYPE(_outputs->type) != CV_32FC1 &&
CV_MAT_TYPE(_outputs->type) != CV_64FC1) ||
_outputs->cols != layer_sizes->data.i[layer_sizes->cols - 1] )
CV_ERROR( CV_StsBadArg,
"output training data should be a floating-point matrix with"
"the number of rows equal to the number of training samples and "
"the number of columns equal to the size of last (output) layer" );
//确保样本的输入和输出的数量一致,即每个样本都必须有一个响应值或分类标签
if( _inputs->rows != _outputs->rows )
CV_ERROR( CV_StsUnmatchedSizes, "The numbers of input and output samples do not match" );
//如果定义了_sample_idx,则需要掩码一些样本数据
if( _sample_idx )
//得到真正用于训练的样本
CV_CALL( sample_idx = cvPreprocessIndexArray( _sample_idx, _inputs->rows ));
sidx = sample_idx->data.i; //指针赋值
count = sample_idx->cols + sample_idx->rows - 1; //得到训练样本的数量
else
count = _inputs->rows; //得到训练样本的数量
if( _sample_weights ) //如果定义了_sample_weights
if( !CV_IS_MAT(_sample_weights) ) //确保_sample_weights格式正确
CV_ERROR( CV_StsBadArg, "sample_weights (if passed) must be a valid matrix" );
sw_type = CV_MAT_TYPE(_sample_weights->type); //数据类型
sw_count = _sample_weights->cols + _sample_weights->rows - 1; //数量
//判断sw_type格式是否正确,sw_count是否与样本的数量一致
if( (sw_type != CV_32FC1 && sw_type != CV_64FC1) ||
(_sample_weights->cols != 1 && _sample_weights->rows != 1) ||
(sw_count != count && sw_count != _inputs->rows) )
CV_ERROR( CV_StsBadArg,
"sample_weights must be 1d floating-point vector containing weights "
"of all or selected training samples" );
sw_step = CV_IS_MAT_CONT(_sample_weights->type) ? 1 :
_sample_weights->step/CV_ELEM_SIZE(sw_type); //得到步长
CV_CALL( sw = (double*)cvAlloc( count*sizeof(sw[0]) )); //为sw分配空间
//为MLP的输入和输出数据开辟一块内存空间
CV_CALL( ivecs.data.ptr = (uchar**)cvAlloc( count*sizeof(ivecs.data.ptr[0]) ));
CV_CALL( ovecs.data.ptr = (uchar**)cvAlloc( count*sizeof(ovecs.data.ptr[0]) ));
ivecs.type = CV_MAT_TYPE(_inputs->type); //指定类型
ovecs.type = CV_MAT_TYPE(_outputs->type); //指定类型
ivecs.count = ovecs.count = count; //相量的长度,即维数
for( i = 0; i < count; i++ ) //遍历所有的待训练样本数据
int idx = sidx ? sidx[i] : i; //表示样本索引值
//给MLP的输入和输出数据赋值
ivecs.data.ptr[i] = _inputs->data.ptr + idx*_inputs->step;
ovecs.data.ptr[i] = _outputs->data.ptr + idx*_outputs->step;
if( sw ) //如果sw被定义
int si = sw_count == count ? i : idx; //得到样本索引值
double w = sw_type == CV_32FC1 ? //得到当前样本的权值
(double)_sample_weights->data.fl[si*sw_step] :
_sample_weights->data.db[si*sw_step];
sw[i] = w; //赋值
if( w < 0 ) //权值不能小于0
CV_ERROR( CV_StsOutOfRange, "some of sample weights are negative" );
sw_sum += w; //权值累加
// normalize weights
if( sw ) //如果sw被定义,归一化样本权值
sw_sum = sw_sum > DBL_EPSILON ? 1./sw_sum : 0; //倒数
for( i = 0; i < count; i++ )
sw[i] *= sw_sum; //归一化
//调用calc_input_scale和calc_output_scale函数,依据_flags分别对输入数据(样本值)和输出数据(样本响应值)进行规范化处理,这两个函数在后面给出详细的介绍
calc_input_scale( &ivecs, _flags );
CV_CALL( calc_output_scale( &ovecs, _flags ));
ok = true; //标识函数返回值
__END__;
if( !ok ) //没有正确对训练过程进行预处理,则清空一些变量
cvFree( &ivecs.data.ptr );
cvFree( &ovecs.data.ptr );
cvFree( &sw );
cvReleaseMat( &sample_idx ); //释放空间
*_ivecs = ivecs; //赋值
*_ovecs = ovecs; //赋值
*_sw = sw; //赋值
return ok;
对输入数据进行规范化处理:
void CvANN_MLP::calc_input_scale( const CvVectors* vecs, int flags )
//vecs表示MLP的输入层数据,即样本
//flags为UPDATE_WEIGHTS、NO_INPUT_SCALE或NO_OUTPUT_SCALE
// reset_weights表示没有定义UPDATE_WEIGHTS
bool reset_weights = (flags & UPDATE_WEIGHTS) == 0;
// no_scale表示定义了NO_INPUT_SCALE
bool no_scale = (flags & NO_INPUT_SCALE) != 0;
double* scale = weights[0]; //表示输入层规范化所用到的系数
int count = vecs->count; //表示样本数据的数量
//没有定义UPDATE_WEIGHTS,则权值需要初始化
if( reset_weights )
//vcount表示MLP输入层的神经元数量,即样本的特征属性的数量
int i, j, vcount = layer_sizes->data.i[0];
int type = vecs->type; //输入数据的类型
//定义了NO_INPUT_SCALE,则a为1,否则为0
double a = no_scale ? 1. : 0.;
//遍历所有的特征属性,初始化数组scale,即weights[0],weights[0]空间大小为vcount×2
for( j = 0; j < vcount; j++ )
scale[2*j] = a, scale[j*2+1] = 0.;
//定义了NO_INPUT_SCALE,则无需后面的操作,函数直接返回
if( no_scale )
return;
for( i = 0; i < count; i++ ) //遍历所有的样本
//得到当前样本的两种不同数据类型的形式
const float* f = vecs->data.fl[i];
const double* d = vecs->data.db[i];
for( j = 0; j < vcount; j++ ) //遍历所有的特征属性
//如果数据类型是CV_32F,则用f,否则用d,t为当前的特征属性值
double t = type == CV_32F ? (double)f[j] : d[j];
scale[j*2] += t; //累加所有样本的当前特征属性值
scale[j*2+1] += t*t; //平方累加所有样本的当前特征属性值
//再次遍历所有的特征属性,使特征属性规范化为均值为0,标准方差为1的值
for( j = 0; j < vcount; j++ )
double s = scale[j*2], s2 = scale[j*2+1];
double m = s/count, sigma2 = s2/count - m*m;
scale[j*2] = sigma2 < DBL_EPSILON ? 1 : 1./sqrt(sigma2);
scale[j*2+1] = -m*scale[j*2];
对输出数据进行规范化处理:
void CvANN_MLP::calc_output_scale( const CvVectors* vecs, int flags )
//vecs表示MLP的输出层数据,即样本的响应值
//flags为UPDATE_WEIGHTS、NO_INPUT_SCALE或NO_OUTPUT_SCALE
//vcount表示MLP输出层的神经元数量
int i, j, vcount = layer_sizes->data.i[layer_sizes->cols-1];
int type = vecs->type; //样本响应值的类型
double m = min_val, M = max_val, m1 = min_val1, M1 = max_val1;
// reset_weights表示没有定义UPDATE_WEIGHTS
bool reset_weights = (flags & UPDATE_WEIGHTS) == 0;
// no_scale表示定义了NO_OUTPUT_SCALE
bool no_scale = (flags & NO_OUTPUT_SCALE) != 0;
int l_count = layer_sizes->cols; //MLP的层数
// scale和inv_scale都表示输出层规范化所用到的系数,两者互为倒数
double* scale = weights[l_count];
double* inv_scale = weights[l_count+1];
int count = vecs->count; //样本数量
CV_FUNCNAME( "CvANN_MLP::calc_output_scale" );
__BEGIN__;
//没有定义UPDATE_WEIGHTS
if( reset_weights )
double a0 = no_scale ? 1 : DBL_MAX, b0 = no_scale ? 0 : -DBL_MAX;
for( j = 0; j < vcount; j++ ) //先初始化输出层规范化系数
scale[2*j] = inv_scale[2*j] = a0;
scale[j*2+1] = inv_scale[2*j+1] = b0;
//定义了NO_OUTPUT_SCALE,则无需后面的操作,函数直接返回
if( no_scale )
EXIT;
for( i = 0; i < count; i++ ) //遍历所有样本
//得到当前样本的两种不同数据类型的形式
const float* f = vecs->data.fl[i];
const double* d = vecs->data.db[i];
for( j = 0; j < vcount; j++ ) //遍历所有的输出层神经元
//如果数据类型是CV_32F,则用f,否则用d
double t = type == CV_32F ? (double)f[j] : d[j];
if( reset_weights ) //没有定义UPDATE_WEIGHTS
double mj = scale[j*2], Mj = scale[j*2+1];
if( mj > t ) mj = t; //得到最小值
if( Mj < t ) Mj = t; //得到最大值
scale[j*2] = mj; //赋值
scale[j*2+1] = Mj; //赋值
else //定义了UPDATE_WEIGHTS
//计算一个新的值,并判断该是否在要求的范围内
t = t*inv_scale[j*2] + inv_scale[2*j+1];
if( t < m1 || t > M1 )
CV_ERROR( CV_StsOutOfRange,
"Some of new output training vector components run exceed the original range too much" );
if( reset_weights ) //没有定义UPDATE_WEIGHTS
//遍历所有输出层的神经元,计算输出层的规范化系数
for( j = 0; j < vcount; j++ )
// map mj..Mj to m..M
double mj = scale[j*2], Mj = scale[j*2+1];
double a, b;
double delta = Mj - mj;
if( delta < DBL_EPSILON )
a = 1, b = (M + m - Mj - mj)*0.5;
else
a = (M - m)/delta, b = m - mj*a;
inv_scale[j*2] = a; inv_scale[j*2+1] = b;
a = 1./a; b = -b*a;
scale[j*2] = a; scale[j*2+1] = b;
__END__;
初始化权值:
void CvANN_MLP::init_weights()
int i, j, k;
for( i = 1; i < layer_sizes->cols; i++ ) //遍历除输入层以外的MLP的所有层
int n1 = layer_sizes->data.i[i-1]; //当前层的前一层的神经元的数量
int n2 = layer_sizes->data.i[i]; //当前层的神经元的数量
//val表示正负1之间的一个随机的数,G为式39中的G
double val = 0, G = n2 > 2 ? 0.7*pow((double)n1,1./(n2-1)) : 1.;
double* w = weights[i]; //w表示当前层的权值
// initialize weights using Nguyen-Widrow algorithm
//利用Nguyen-Widrow算法初始化权值
for( j = 0; j < n2; j++ ) //遍历当前层的所有神经元
double s = 0;
for( k = 0; k <= n1; k++ ) //遍历连接当前神经元的所有权值,包括偏移量
val = rng->uniform(0., 1.)*2-1.; //得到正负1之间的一个随机数
w[k*n2 + j] = val; //权值先赋一个初始值
s += fabs(val); //计算所有随机数的累计和
//如果当前层不是最后一层,即输出层,而输出层的权值由上面的for循环直接得到
if( i < layer_sizes->cols - 1 )
//把偏移量的随机数去掉后,得到式37的分母部分
s = 1./(s - fabs(val));
for( k = 0; k <= n1; k++ )
w[k*n2 + j] *= s; //得到中间层的初始权值,即式37
w[n1*n2 + j] *= G*(-1+j*2./n2); //得到偏移量的初始值,即式38
BACKPROP算法的具体训练过程:
int CvANN_MLP::train_backprop( CvVectors x0, CvVectors u, const double* sw )
//x0表示输入样本
//u表示样本响应值
//sw表示样本的权值
CvMat* dw = 0;
CvMat* buf = 0;
double **x = 0, **df = 0;
CvMat* _idx = 0;
//iter表示训练MLP所需的迭代次数,count表示训练样本的数量
int iter = -1, count = x0.count;
CV_FUNCNAME( "CvANN_MLP::train_backprop" );
__BEGIN__;
//ivcount表示输入层的神经元的数量,ovcount表示输出层的神经元的数量,l_count表示MLP的层数,total表示MLP模型的所有神经元的数量,max_iter表示
int i, j, k, ivcount, ovcount, l_count, total = 0, max_iter;
double *buf_ptr; //该指针指向矩阵buf
//E表示误差,prev_E表示前一次迭代的误差
double prev_E = DBL_MAX*0.5, E = 0, epsilon;
//得到最大迭代次数,乘以count表示每个样本都要计算
max_iter = params.term_crit.max_iter*count;
epsilon = params.term_crit.epsilon*count; //得到两次迭代的最小误差变化
l_count = layer_sizes->cols; //得到MLP的层数
ivcount = layer_sizes->data.i[0]; //得到输入层的神经元的数量
ovcount = layer_sizes->data.i[l_count-1]; //得到输出层的神经元的数量
// allocate buffers
//得到MLP模型的所有神经元的数量
for( i = 0; i < l_count; i++ )
total += layer_sizes->data.i[i] + 1;
//定义矩阵dw的大小及数据类型,与wbuf一致,dw表示权值的变化率
CV_CALL( dw = cvCreateMat( wbuf->rows, wbuf->cols, wbuf->type ));
cvZero( dw ); //dw矩阵初始化为0
//定义矩阵buf的大小及数据类型,表示所有神经元及样本的存储空间
CV_CALL( buf = cvCreateMat( 1, (total + max_count)*2, CV_64F ));
//定义矩阵_idx的大小及数据类型,表示样本索引
CV_CALL( _idx = cvCreateMat( 1, count, CV_32SC1 ));
for( i = 0; i < count; i++ )
_idx->data.i[i] = i; //初始化_idx
//为x分配内存空间,表示所有神经元
CV_CALL( x = (double**)cvAlloc( total*2*sizeof(x[0]) ));
df = x + total; //赋予指针df的具体指向,表示激活函数的导数
buf_ptr = buf->data.db; //定义指针
for( j = 0; j < l_count; j++ ) //遍历所有MLP的层
x[j] = buf_ptr; //当前层的x指针指向对应的buf空间的相应位置
df[j] = x[j] + layer_sizes->data.i[j]; //当前层的df指针指向x的下一层
buf_ptr += (df[j] - x[j])*2; //移动buf的指针
// run back-propagation loop
/*
y_i = w_i*x_i-1
x_i = f(y_i)
E = 1/2*||u - x_N||^2
grad_N = (x_N - u)*f'(y_i)
dw_i(t) = momentum*dw_i(t-1) + dw_scale*x_i-1*grad_i
w_i(t+1) = w_i(t) + dw_i(t)
grad_i-1 = w_i^t*grad_i
*/
for( iter = 0; iter < max_iter; iter++ ) //进入MLP算法的迭代
int idx = iter % count; //得到当前训练样本的索引
double* w = weights[0]; //表示输入层规范化系数
double sweight = sw ? count*sw[idx] : 1.; //得到样本权值
CvMat _w, _dw, hdr1, hdr2, ghdr1, ghdr2, _df;
CvMat *x1 = &hdr1, *x2 = &hdr2, *grad1 = &ghdr1, *grad2 = &ghdr2, *temp;
//如果样本是当前迭代的第一个训练样本,则需要判断是否满足迭代的终止条件,并且要打乱样本的次序
if( idx == 0 )
//printf("%d. E = %g\\n", iter/count, E);
//比较两次误差的变化率,如果满足要求,则退出迭代
if( fabs(prev_E - E) < epsilon )
break;
prev_E = E; //重新赋值
E = 0; //初始化当前误差为0
// shuffle indices
//遍历所有的样本,打乱样本的先后次序
for( i = 0; i < count; i++ )
int tt;
j = (*rng)(count); //得到两个小于count的随机数
k = (*rng)(count);
CV_SWAP( _idx->data.i[j], _idx->data.i[k], tt ); //交换位置
idx = _idx->data.i[idx]; //真正得到当前的训练样本的索引
//样本进入MLP的输入层
if( x0.type == CV_32F ) //如果样本是CV_32F数据类型
const float* x0data = x0.data.fl[idx]; //得到当前样本
//输入数据进行规范化处理,w[j*2]和w[j*2 + 1]由calc_input_scale函数得到
for( j = 0; j < ivcount; j++ )
x[0][j] = x0data[j]*w[j*2] + w[j*2 + 1];
else //如果样本是CV_64F数据类型
const double* x0data = x0.data.db[idx]; //得到当前样本
//输入数据进行规范化处理,w[j*2]和w[j*2 + 1]由calc_input_scale函数得到
for( j = 0; j < ivcount; j++ )
x[0][j] = x0data[j]*w[j*2] + w[j*2 + 1];
//初始化矢量x1,x1表示输入层的输出
cvInitMatHeader( x1, 1, ivcount, CV_64F, x[0] );
// forward pass, compute y[i]=w*x[i-1], x[i]=f(y[i]), df[i]=f'(y[i])
//前向传播步骤,遍历所有的层,得到当前样本经MLP处理后的输出
for( i = 1; i < l_count; i++ )
//初始化矢量x2,x2表示当前层输出
cvInitMatHeader( x2, 1, layer_sizes->data.i[i], CV_64F, x[i] );
//初始化矩阵_w,它表示权值wkhl
cvInitMatHeader( &_w, x1->cols, x2->cols, CV_64F, weights[i] );
//实现x1×&_w=x2,即式16,这里的x2为加权和
cvGEMM( x1, &_w, 1, 0, 0, x2 );
_df = *x2; //赋值指针
_df.data.db = df[i]; //赋值指针
//计算激活函数及它的导数,该函数在后面给出详细的介绍
calc_activ_func_deriv( x2, &_df, _w.data.db + _w.rows*_w.cols );
//交换x1和x2的位置,即此次的输出作为下次的输入
CV_SWAP( x1, x2, temp );
//初始化矢量grad1,它表示式30的δ
cvInitMatHeader( grad1, 1, ovcount, CV_64F, buf_ptr );
*grad2 = *grad1; //变量赋值,两者具有相同的类型
grad2->data.db = buf_ptr + max_count; //定义grad2的指针
w = weights[l_count+1]; //w表示输出规范化所用到的系数
// calculate error
//计算输出层误差
if( u.type == CV_32F ) //如果样本响应值是CV_32F数据类型
const float* udata = u.data.fl[idx]; //得到当前样本的响应值
//遍历输出层的所有神经元,即样本的所有可能值
for( k = 0; k < ovcount; k++ )
//udata[k]*w[k*2] + w[k*2+1]表示规范化后的输出层的输出,w[k*2]和w[k*2+1]由calc_output_scale函数得到
double t = udata[k]*w[k*2] + w[k*2+1] - x[l_count-1][k]; //得到误差
grad1->data.db[k] = t*sweight; //误差乘以样本权值
E += t*t; //误差平方的累加,式10
else //如果样本响应值是CV_64F数据类型
const double* udata = u.data.db[idx]; //得到当前样本的响应值
//遍历输出层的所有神经元,即样本的所有可能值
for( k = 0; k < ovcount; k++ )
//udata[k]*w[k*2] + w[k*2+1]表示规范化后的输出层的输出,w[k*2]和w[k*2+1]由calc_output_scale函数得到
double t = udata[k]*w[k*2] + w[k*2+1] - x[l_count-1][k]; //得到误差
grad1->data.db[k] = t*sweight; //误差乘以样本权值
E += t*t; //误差平方的累加,式10
E *= sweight; //再乘以样本权值
// backward pass, update weights
//反向步骤,计算权值的变化率及更新权值
for( i = l_count-1; i > 0; i-- ) //遍历MLP的所有层,输入层除外
//n1为前一层的神经元的数量,n2为当前层的神经元的数量
int n1 = layer_sizes->data.i[i-1], n2 = layer_sizes->data.i[i];
//初始化矩阵_df,它指向df[i],表示激活函数的导数
cvInitMatHeader( &_df, 1, n2, CV_64F, df[i] );
//实现grad1和&_df中的对应元素相乘,并再次赋值给grad1,即得到式36的δkl
cvMul( grad1, &_df, grad1 );
//初始化矩阵_w,它表示权值
cvInitMatHeader( &_w, n1+1, n2, CV_64F, weights[i] );
//初始化矩阵_dw,它表示权值的变化率
cvInitMatHeader( &_dw, n1+1, n2, CV_64F, dw->data.db + (weights[i] - weights[0]) );
//初始化x1,它表示前一层的输出
cvInitMatHeader( x1, n1+1, 1, CV_64F, x[i-1] );
x[i-1][n1] = 1.; //初始化为1,它的含义就相当于式2中x0
//实现params.bp_dw_scale×x1×grad1+params.bp_moment_scale×&_dw=&_dw,即式12
cvGEMM( x1, grad1, params.bp_dw_scale, &_dw, params.bp_moment_scale, &_dw );
//实现&_w+&_dw=&_w,即式13
cvAdd( &_w, &_dw, &_w );
if( i > 1 ) //计算中间层的式36中的∑kwδ部分
grad2->cols = n1; //前一层的神经元数量
_w.rows = n1; //权值的行
//实现了grad1×(&_w的转置)= grad2,即得到式36中的∑kwδ部分
cvGEMM( grad1, &_w, 1, 0, 0, grad2, CV_GEMM_B_T );
//交换grad1和grad2的位置,即下次循环用grad1
CV_SWAP( grad1, grad2, temp );
iter /= count; //得到真正的迭代次数
__END__;
//释放内存空间
cvReleaseMat( &dw );
cvReleaseMat( &buf );
cvReleaseMat( &_idx );
cvFree( &x );
return iter; //返回迭代次数
计算激活函数,及它的导数:
void CvANN_MLP::calc_activ_func_deriv( CvMat* _xf, CvMat* _df,
const double* bias ) const
//_xf作为输入变量表示式15中的∑部分,经该函数处理后该变量表示激活函数的结果,即式14中的ykl
//_df表示激活函数的导数
//bias表示偏移量,即式15中的bkl
//n其实就是1,cols表示该层的神经元的数量
int i, j, n = _xf->rows, cols = _xf->cols;
double* xf = _xf->data.db; //指针赋值
double* df = _df->data.db; //指针赋值
//scale表示由激活函数的参数α得到常数,scale2表示激活函数的参数β
double scale, scale2 = f_param2;
//确保_xf和_df的类型一致
assert( CV_IS_MAT_CONT( _xf->type & _df->type ) );
if( activ_func == IDENTITY ) //线性激活函数
for( i = 0; i < n; i++, xf += cols, df += cols )
for( j = 0; j < cols; j++ ) //遍历该层的所有神经元
xf[j] += bias[j]; //加上偏移量后,得到激活函数的输出结果
df[j] = 1; //线性激活函数的导数,式23
return;
else if( activ_func == GAUSSIAN ) //高斯激活函数
scale = -f_param1*f_param1; //得到-α2
scale2 *= scale; //得到-α2β
for( i = 0; i < n; i++, xf += cols, df += cols )
for( j = 0; j < cols; j++ ) //遍历该层的所有神经元
double t = xf[j] + bias[j]; //加上偏移量后,得到激活函数的输入
df[j] = t*2*scale2; //得到-2α2βx
xf[j] = t*t*scale; //得到-α2x2
cvExp( _xf, _xf ); //计算式9中的e指数部分
n *= cols; //其实就等于cols
xf -= n; df -= n; //重新定义xf和df的指针
for( i = 0; i < n; i++ )
df[i] *= xf[i]; //得到激活函数的导数,即式27
else //对称Sigmoid激活函数
scale = f_param1; //参数α
for( i = 0; i < n; i++, xf += cols, df += cols )
for( j = 0; j < cols; j++ ) //遍历该层的所有神经元
xf[j] = (xf[j] + bias[j])*scale; //得到αx,其中x包含偏移量
df[j] = -fabs(xf[j]); //得到-|αx|
cvExp( _df, _df ); //得到式7中的e指数部分
n *= cols; //其实就等于cols
xf -= n; df -= n; //重新定义xf和df的指针
// ((1+exp(-ax))^-1)'=a*((1+exp(-ax))^-2)*exp(-ax);
// ((1-exp(-ax))/(1+exp(-ax)))'=(a*exp(-ax)*(1+exp(-ax)) + a*exp(-ax)*(1-exp(-ax)))/(1+exp(-ax))^2=
// 2*a*exp(-ax)/(1+exp(-ax))^2
scale *= 2*f_param2; //得到2αβ
for( i = 0; i < n; i++ )
//如果αx大于0,则s0为1,否则为-1
int s0 = xf[i] > 0 ? 1 : -1;
double t0 = 1./(1. + df[i]); //得到式25中的分母部分
double t1 = scale*df[i]*t0*t0; //得到式25
t0 *= scale2*(1. - df[i])*s0; //得到式7,但要根据αx赋予正负号
df[i] = t1; //激活函数的导数
xf[i] = t0; //激活函数的结果输出
RPROP算法的具体训练过程:
int CvANN_MLP::train_rprop( CvVectors x0, CvVectors u, const double* sw )
const int max_buf_size = 1 << 16;
CvMat* dw = 0;
CvMat* dEdw = 0;
CvMat* prev_dEdw_sign = 0;
CvMat* buf = 0;
double **x = 0, **df = 0;
int iter = -1, count = x0.count; //count表示样本的数量
CV_FUNCNAME( "CvANN_MLP::train" );
__BEGIN__;
int i, ivcount, ovcount, l_count, total = 0, max_iter, buf_sz, dcount0;
double *buf_ptr;
double prev_E = DBL_MAX*0.5, epsilon;
double dw_plus, dw_minus, dw_min, dw_max;
double inv_count;
max_iter = params.term_crit.max_iter;
epsilon = params.term_crit.epsilon;
dw_plus = params.rp_dw_plus;
dw_minus = params.rp_dw_minus;
dw_min = params.rp_dw_min;
dw_max = params.rp_dw_max;
l_count = layer_sizes->cols; //得到MLP的层数
ivcount = layer_sizes->data.i[0]; //得到输入层的神经元的数量
ovcount = layer_sizes->data.i[l_count-1]; //得到输出层的神经元的数量
// allocate buffers
for( i = 0; i < l_count; i++ )
total += layer_sizes->data.i[i]; //统计所有神经元的数量
//初始化矩阵dw,它表示式41中的Δ(t)
CV_CALL( dw = cvCreateMat( wbuf->rows, wbuf->cols, wbuf->type ));
cvSet( dw, cvScalarAll(params.rp_dw0) ); //初始化Δ(0)
//初始化dEdw,它表示误差变化率,即∂E/∂w
CV_CALL( dEdw = cvCreateMat( wbuf->rows, wbuf->cols, wbuf->type ));
cvZero( dEdw ); //dEdw清零
//初始化prev_dEdw_sign,它表示上一次∂E/∂w的符号
CV_CALL( prev_dEdw_sign = cvCreateMat( wbuf->rows, wbuf->cols, CV_8SC1 ));
cvZero( prev_dEdw_sign ); //prev_dEdw_sign清零
inv_count = 1./count; //得到样本数量的倒数
dcount0 = max_buf_size/(2*total); // dcount0表以上是关于Opencv2.4.9源码分析——Neural Networks的主要内容,如果未能解决你的问题,请参考以下文章