大数运算和大数类
Posted 松狮MVP
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了大数运算和大数类相关的知识,希望对你有一定的参考价值。
1、首先看一个小问题:
整型数组、字符型数组、vector在未初始化的情况下:
int main()
int data[5];
char c[5];
vector<int> v(5);
vector<char> v1(5);
vector<int> v2;
cout << "int[]: ";
for (int i = 0; i < 5; i++)
cout << data[i] << " ";
cout << endl << endl;
cout << "char[]: ";
for (int i = 0; i < 5; i++)
cout << c[i] << ",";
cout << endl << endl;
cout << "vector(int): ";
for (int i : v)
cout << i << " ";
cout << endl << endl;
cout << "vector(char): ";
for (auto i : v1)
cout << i << ",";
cout << endl << endl;
cout << "vector: ";
for (int i : v2)
cout << i << ",";
cout << endl << endl;
return 0;
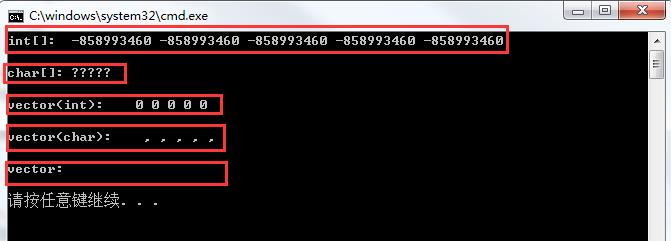
vs测试结果:
(1)整型数组在未初始化时,内存中是乱码;
(2)字符型数组在未初始化时,内存中是乱码;
(3)vector指定容量,int型时,初始化为0;
(4)vector指定容量,char型时,初始化为可打印的空白字符;
(5)vector不指定容量,默认0;
2、简单的大数相加:
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
#define N 500
//25369874522455633 + 68452156965
void bigNumAdd(string a, string b)
int carry = 0; //表示进位
//字符串反转(真正的数字位数 和 字符串下标 刚好是相反的,加法应该从数字低位算起) 且 字符串变数字
int m[N] = 0 ;
int n[N] = 0 ;
int len1 = a.length(), len2 = b.length();
for (int i = 0; i < len1; i++)
m[i] = a[len1 - i - 1] - '0'; //加法应该从数字低位算起
for (int i = 0; i < len2; i++)
n[i] = b[len2 - i - 1] - '0'; //加法应该从数字低位算起
//位运算————加法应该从数字低位算起
int len = len1>len2 ? len1 + 1 : len2 + 1;
string sum(len, 0);
int k;
for (k = 0; k < len1 || k < len2; k++)
sum[k] = (m[k] + n[k] + carry) % 10 + '0';
carry = (m[k] + n[k] + carry) / 10;
//处理最高位进位
if (carry)
sum[k] = carry + '0';
//结果字符串反转 并 输出
reverse(sum.begin(), sum.end());
cout << sum << endl;
int main()
string a, b;
cin >> a >> b;
bigNumAdd(a, b);
return 0;
转自:http://blog.csdn.net/hackbuteer1/article/details/6595881
#include<iostream>
#include<string>
#include<iomanip>
#include<algorithm>
using namespace std;
#define MAXN 9999
#define MAXSIZE 10
#define DLEN 4
class BigNum
private:
int a[500]; //可以控制大数的位数
int len; //大数长度
public:
BigNum() len = 1;memset(a,0,sizeof(a)); //构造函数
BigNum(const int); //将一个int类型的变量转化为大数
BigNum(const char*); //将一个字符串类型的变量转化为大数
BigNum(const BigNum &); //拷贝构造函数
BigNum &operator=(const BigNum &); //重载赋值运算符,大数之间进行赋值运算
friend istream& operator>>(istream&, BigNum&); //重载输入运算符
friend ostream& operator<<(ostream&, BigNum&); //重载输出运算符
BigNum operator+(const BigNum &) const; //重载加法运算符,两个大数之间的相加运算
BigNum operator-(const BigNum &) const; //重载减法运算符,两个大数之间的相减运算
BigNum operator*(const BigNum &) const; //重载乘法运算符,两个大数之间的相乘运算
BigNum operator/(const int &) const; //重载除法运算符,大数对一个整数进行相除运算
BigNum operator^(const int &) const; //大数的n次方运算
int operator%(const int &) const; //大数对一个int类型的变量进行取模运算
bool operator>(const BigNum & T)const; //大数和另一个大数的大小比较
bool operator>(const int & t)const; //大数和一个int类型的变量的大小比较
void print(); //输出大数
;
BigNum::BigNum(const int b) //将一个int类型的变量转化为大数
int c,d = b;
len = 0;
memset(a,0,sizeof(a));
while(d > MAXN)
c = d - (d / (MAXN + 1)) * (MAXN + 1);
d = d / (MAXN + 1);
a[len++] = c;
a[len++] = d;
BigNum::BigNum(const char*s) //将一个字符串类型的变量转化为大数
int t,k,index,l,i;
memset(a,0,sizeof(a));
l=strlen(s);
len=l/DLEN;
if(l%DLEN)
len++;
index=0;
for(i=l-1;i>=0;i-=DLEN)
t=0;
k=i-DLEN+1;
if(k<0)
k=0;
for(int j=k;j<=i;j++)
t=t*10+s[j]-'0';
a[index++]=t;
BigNum::BigNum(const BigNum & T) : len(T.len) //拷贝构造函数
int i;
memset(a,0,sizeof(a));
for(i = 0 ; i < len ; i++)
a[i] = T.a[i];
BigNum & BigNum::operator=(const BigNum & n) //重载赋值运算符,大数之间进行赋值运算
int i;
len = n.len;
memset(a,0,sizeof(a));
for(i = 0 ; i < len ; i++)
a[i] = n.a[i];
return *this;
istream& operator>>(istream & in, BigNum & b) //重载输入运算符
char ch[MAXSIZE*4];
int i = -1;
in>>ch;
int l=strlen(ch);
int count=0,sum=0;
for(i=l-1;i>=0;)
sum = 0;
int t=1;
for(int j=0;j<4&&i>=0;j++,i--,t*=10)
sum+=(ch[i]-'0')*t;
b.a[count]=sum;
count++;
b.len =count++;
return in;
ostream& operator<<(ostream& out, BigNum& b) //重载输出运算符
int i;
cout << b.a[b.len - 1];
for(i = b.len - 2 ; i >= 0 ; i--)
cout.width(DLEN);
cout.fill('0');
cout << b.a[i];
return out;
BigNum BigNum::operator+(const BigNum & T) const //两个大数之间的相加运算
BigNum t(*this);
int i,big; //位数
big = T.len > len ? T.len : len;
for(i = 0 ; i < big ; i++)
t.a[i] +=T.a[i];
if(t.a[i] > MAXN)
t.a[i + 1]++;
t.a[i] -=MAXN+1;
if(t.a[big] != 0)
t.len = big + 1;
else
t.len = big;
return t;
BigNum BigNum::operator-(const BigNum & T) const //两个大数之间的相减运算
int i,j,big;
bool flag;
BigNum t1,t2;
if(*this>T)
t1=*this;
t2=T;
flag=0;
else
t1=T;
t2=*this;
flag=1;
big=t1.len;
for(i = 0 ; i < big ; i++)
if(t1.a[i] < t2.a[i])
j = i + 1;
while(t1.a[j] == 0)
j++;
t1.a[j--]--;
while(j > i)
t1.a[j--] += MAXN;
t1.a[i] += MAXN + 1 - t2.a[i];
else
t1.a[i] -= t2.a[i];
t1.len = big;
while(t1.a[t1.len - 1] == 0 && t1.len > 1)
t1.len--;
big--;
if(flag)
t1.a[big-1]=0-t1.a[big-1];
return t1;
BigNum BigNum::operator*(const BigNum & T) const //两个大数之间的相乘运算
BigNum ret;
int i,j,up;
int temp,temp1;
for(i = 0 ; i < len ; i++)
up = 0;
for(j = 0 ; j < T.len ; j++)
temp = a[i] * T.a[j] + ret.a[i + j] + up;
if(temp > MAXN)
temp1 = temp - temp / (MAXN + 1) * (MAXN + 1);
up = temp / (MAXN + 1);
ret.a[i + j] = temp1;
else
up = 0;
ret.a[i + j] = temp;
if(up != 0)
ret.a[i + j] = up;
ret.len = i + j;
while(ret.a[ret.len - 1] == 0 && ret.len > 1)
ret.len--;
return ret;
BigNum BigNum::operator/(const int & b) const //大数对一个整数进行相除运算
BigNum ret;
int i,down = 0;
for(i = len - 1 ; i >= 0 ; i--)
ret.a[i] = (a[i] + down * (MAXN + 1)) / b;
down = a[i] + down * (MAXN + 1) - ret.a[i] * b;
ret.len = len;
while(ret.a[ret.len - 1] == 0 && ret.len > 1)
ret.len--;
return ret;
int BigNum::operator %(const int & b) const //大数对一个int类型的变量进行取模运算
int i,d=0;
for (i = len-1; i>=0; i--)
d = ((d * (MAXN+1))% b + a[i])% b;
return d;
BigNum BigNum::operator^(const int & n) const //大数的n次方运算
BigNum t,ret(1);
int i;
if(n<0)
exit(-1);
if(n==0)
return 1;
if(n==1)
return *this;
int m=n;
while(m>1)
t=*this;
for( i=1;i<<1<=m;i<<=1)
t=t*t;
m-=i;
ret=ret*t;
if(m==1)
ret=ret*(*this);
return ret;
bool BigNum::operator>(const BigNum & T) const //大数和另一个大数的大小比较
int ln;
if(len > T.len)
return true;
else if(len == T.len)
ln = len - 1;
while(a[ln] == T.a[ln] && ln >= 0)
ln--;
if(ln >= 0 && a[ln] > T.a[ln])
return true;
else
return false;
else
return false;
bool BigNum::operator >(const int & t) const //大数和一个int类型的变量的大小比较
BigNum b(t);
return *this>b;
void BigNum::print() //输出大数
int i;
cout << a[len - 1];
for(i = len - 2 ; i >= 0 ; i--)
cout.width(DLEN);
cout.fill('0');
cout << a[i];
cout << endl;
int main(void)
int i,n;
BigNum x[101]; //定义大数的对象数组
x[0]=1;
for(i=1;i<101;i++)
x[i]=x[i-1]*(4*i-2)/(i+1);
while(scanf("%d",&n)==1 && n!=-1)
x[n].print();
附录:
#include <iostream>
#include <string>
using namespace std;
int compare(string str1, string str2)
//相等返回0,大于返回1,小于返回-1
if (str1.size()>str2.size()) return 1; //长度长的整数大于长度小的整数
else if (str1.size()<str2.size()) return -1;
else return str1.compare(str2); //若长度相等,则头到尾按位比较
string SUB_INT(string str1, string str2);
string ADD_INT(string str1, string str2) //高精度加法
int sign = 1; //sign 为符号位
string str;
if (str1[0] == '-')
if (str2[0] == '-')
sign = -1;
str = ADD_INT(str1.erase(0, 1), str2.erase(0, 1));
else
str = SUB_INT(str2, str1.erase(0, 1));
else
if (str2[0] == '-')
str = SUB_INT(str1, str2.erase(0, 1));
else //把两个整数对齐,短整数前面加0补齐
string::size_type L1, L2;
int i;
L1 = str1.size();
L2 = str2.size();
if (L1<L2)
for (i = 1; i <= L2 - L1; i++) str1 = "0" + str1;
else
for (i = 1; i <= L1 - L2; i++) str2 = "0" + str2;
int int1 = 0, int2 = 0; //int2 记录进位
for (i = str1.size() - 1; i >= 0; i--)
int1 = (int(str1[i]) - '0' + int(str2[i]) - '0' + int2) % 10;
int2 = (int(str1[i]) - '0' + int(str2[i]) - '0' + int2) / 10;
str = char(int1 + '0') + str;
if (int2 != 0) str = char(int2 + '0') + str;
//运算后处理符号位
if ((sign == -1) && (str[0] != '0')) str = "-" + str;
return str;
string SUB_INT(string str1, string str2) //高精度减法
int sign = 1; //sign 为符号位
string str;
int i, j;
if (str2[0] == '-')
str = ADD_INT(str1, str2.erase(0, 1));
else
int res = compare(str1, str2);
if (res == 0) return "0";
if (res<0)
sign = -1;
string temp = str1;
str1 = str2;
str2 = temp;
string::size_type tempint;
tempint = str1.size() - str2.size();
for (i = str2.size() - 1; i >= 0; i--)
if (str1[i + tempint]<str2[i])
j = 1;
while (1) //zhao4zhong1添加
if (str1[i + tempint - j] == '0')
str1[i + tempint - j] = '9';
j++;
else
str1[i + tempint - j] = char(int(str1[i + tempint - j]) - 1);
break;
str = char(str1[i + tempint] - str2[i] + ':') + str;
else
str = char(str1[i + tempint] - str2[i] + '0') + str;
for (i = tempint - 1; i >= 0; i--) str = str1[i] + str;
//去除结果中多余的前导0
str.erase(0, str.find_first_not_of('0'));
if (str.empty()) str = "0";
if ((sign == -1) && (str[0] != '0')) str = "-" + str;
return str;
string MUL_INT(string str1, string str2) //高精度乘法
int sign = 1; //sign 为符号位
string str;
if (str1[0] == '-')
sign *= -1;
str1 = str1.erase(0, 1);
if (str2[0] == '-')
sign *= -1;
str2 = str2.erase(0, 1);
int i, j;
string::size_type L1, L2;
L1 = str1.size();
L2 = str2.size();
for (i = L2 - 1; i >= 0; i--)
//模拟手工乘法竖式
string tempstr;
int int1 = 0, int2 = 0, int3 = int(str2[i]) - '0';
if (int3 != 0)
for (j = 1; j <= (int)(L2 - 1 - i); j++)
tempstr = "0" + tempstr;
for (j = L1 - 1; j >= 0; j--)
int1 = (int3*(int(str1[j]) - '0') + int2) % 10;
int2 = (int3*(int(str1[j]) - '0') + int2) / 10;
tempstr = char(int1 + '0') + tempstr;
if (int2 != 0) tempstr = char(int2 + '0') + tempstr;
str = ADD_INT(str, tempstr);
//去除结果中的前导0
str.erase(0, str.find_first_not_of('0'));
if (str.empty()) str = "0";
if ((sign == -1) && (str[0] != '0'))
str = "-" + str;
return str;
string DIVIDE_INT(string str1, string str2, int flag) //高精度除法。flag==1时,返回商; flag==0时,返回余数
string quotient, residue; //定义商和余数
int sign1 = 1, sign2 = 1;
if (str2 == "0") //判断除数是否为0
quotient = "ERROR!";
residue = "ERROR!";
if (flag == 1) return quotient;
else return residue;
if (str1 == "0") //判断被除数是否为0
quotient = "0";
residue = "0";
if (str1[0] == '-')
str1 = str1.erase(0, 1);
sign1 *= -1;
sign2 = -1;
if (str2[0] == '-')
str2 = str2.erase(0, 1);
sign1 *= -1;
int res = compare(str1, str2);
if (res<0)
quotient = "0";
residue = str1;
else if (res == 0)
quotient = "1";
residue = "0";
else
string::size_type L1, L2;
L1 = str1.size();
L2 = str2.size();
string tempstr;
tempstr.append(str1, 0, L2 - 1);
for (int i = L2 - 1; i<L1; i++) //模拟手工除法竖式
tempstr = tempstr + str1[i];
tempstr.erase(0, tempstr.find_first_not_of('0'));//zhao4zhong1添加
if (tempstr.empty()) tempstr = "0";//zhao4zhong1添加
for (char ch = '9'; ch >= '0'; ch--) //试商
string str;
str = str + ch;
if (compare(MUL_INT(str2, str), tempstr) <= 0)
quotient = quotient + ch;
tempstr = SUB_INT(tempstr, MUL_INT(str2, str));
break;
residue = tempstr;
//去除结果中的前导0
quotient.erase(0, quotient.find_first_not_of('0'));
if (quotient.empty()) quotient = "0";
if ((sign1 == -1) && (quotient[0] != '0')) quotient = "-" + quotient;
if ((sign2 == -1) && (residue[0] != '0')) residue = "-" + residue;
if (flag == 1) return quotient;
else return residue;
string DIV_INT(string str1, string str2) //高精度除法,返回商
return DIVIDE_INT(str1, str2, 1);
string MOD_INT(string str1, string str2) //高精度除法,返回余数
return DIVIDE_INT(str1, str2, 0);
int main()
/*char ch;
string s1, s2, res;
while (cin >> s1 >> ch >> s2)
switch (ch)
case '+':res = ADD_INT(s1, s2); break;
case '-':res = SUB_INT(s1, s2); break;
case '*':res = MUL_INT(s1, s2); break;
case '/':res = DIV_INT(s1, s2); break;
case '%':res = MOD_INT(s1, s2); break;
default: break;
cout << res << endl;
return(0);*/
string s11, s22, res1;
s11 = "1";
s22 = "2";
for (int i = 1; i <= 1000; i++)
res1 = MUL_INT(s11, s22); //利用乘法做幂次运算!
s11 = res1;
cout << res1 << endl;
return(0);
以上是关于大数运算和大数类的主要内容,如果未能解决你的问题,请参考以下文章