模糊PID基本原理及Simulink仿真实现

Posted 2023-02-19 王张飞

模糊PID基本原理及Simulink仿真实现，向大佬致敬https://blog.csdn.net/qq_41913616/article/details/82020685
以下未说明的都为转载内容转自https://blog.csdn.net/weixin_36340979/article/details/79168052

---

在讲解模糊PID前，我们先要了解PID控制器的原理（本文主要介绍模糊PID的运用,对PID控制器的原理不做详细介绍）。PID控制器（比例-积分-微分控制器）是一个在工业控制应用中常见的反馈回路部件，由比例单元P、积分单元I和微分单元D组成。PID控制的基础是比例控制；积分控制可消除稳态误差，但可能增加超调；微分控制可加快大惯性系统响应速度以及减弱超调趋势。

1.1传统PID控制

传统PID控制器自出现以来，凭借其结构简单、稳定性好、工作可靠、调整方便等优点成为工业控制主要技术。当被控对象的结构和参数具有一定的不确定性，无法对其建立精确的模型时，采用PID控制技术尤为方便。PID控制原理简单、易于实现，但是其参数整定异常麻烦。对于小车的速度控制系统而言，由于其为时变非线性系统不同时刻需要选用不同的PID参数，采用传统的PID控制器，很难使整个运行过程具有较好的运行效果。

1.2模糊PID控制

模糊PID控制，即利用模糊逻辑并根据一定的模糊规则对PID的参数进行实时的优化，以克服传统PID参数无法实时调整PID参数的缺点。模糊PID控制包括模糊化，确定模糊规则，解模糊等组成部分。小车通过传感器采集赛道信息，确定当前距赛道中线的偏差E以及当前偏差和上次偏差的变化ec，根据给定的模糊规则进行模糊推理，最后对模糊参数进行解模糊，输出PID控制参数。

2.1模糊化

模糊控制器主要由三个模块组成：模糊化，模糊推理，清晰化。具体如下图所示。而我们将一步步讲解如何将模糊PID算法运用到智能车上。（最好用笔一步步自己写一遍！！！）

首先我们的智能车会采集到赛道的相关数据，例如摄像头车，其采集到的数据经过算法处理之后会得到与中线的偏差E，以及当前偏差和上次偏差的变化（差值）EC两个值（即此算法为2维输入，同理也可以是1维和3维，但2维更适合智能车）。例如此时车偏离中线的距离为150，而上一时刻偏离中线的距离为120，则E为150，EC为150 - 120 = 30。

其次我们要对这两个值进行模糊化。这里我们对E进行举例。摄像头车采集回来的E是有范围的，即与中线的偏差是在一个区间内可行的。在这里我们假设该区间为-240到240，即小车偏离中线的最大距离为240，正负即为左右。再假设中线偏差变化率的可行区间为-40到+40。

接着我们要对这两个值进行模糊化。我现在将E的区间（-240 到 240）分成8个部分，那么他们分别为-240 ~ -180，-180 ~ -120 ，-120 ~ -60，-60 ~ 0，0 ~ 60，60 ~ 120，120 ~ 180，180 ~ 240。然后我们把-180，-120，-60，0，60，120，180分别用NB，NM，NS，ZO，PS，PM，PB表示（个人理解N为negative，P为positive，B为big，M为middle，S为small，ZO为zero）。例如，当E = 170时，此时的E属于PM和PB之间，而此时的E也会对应2（或1）个隶属度。E隶属于PM（120）的百分比为（180 - 170） / （180 - 120） = 1 / 6 ，而同理隶属于PB（180）的百分比为（170 - 120） / （180 - 120） = 5 / 6 。意思就是120到180进行线性分割了，E离PM和PB哪个更近，则隶属于哪个就更大（当输出值E大于180（PB）时，则隶属度为1，隶属度值为PB，即E完全隶属于PB，同理当E小于 - 180 （NB）时也一样）。同理也可以对EC进行模糊化。

2.2 模糊推理

对于采集回来的E和EC，我们可以推出它们各所占的隶属度，此时我们可以根据模糊规则表去找出输出值所对应的隶属度。

我们假设为E的两个隶属度值为PM、PB,E属于PM的隶属度为a（a < 1），则属于PB的隶属度为（1 - a）。再假设EC的两个隶属度值为NB、NM，EC属于NM的隶属度为b，则属于NB的隶属度为（1 - b）。而在假设中，E属于PM的隶属度为a，EC属于NB的隶属度为( 1 - b )，则输出值属于ZO的隶属度为a *( 1 - b )（看图）。

同理我们可以得出，当输出值属于ZO的另外两个隶属度为a \\* b， （ 1 - a ） \\* （ 1 - b） ，而输出值属于NS的隶属度为（ 1 - a ） \\* 1 - b。
在这里我们先证明一个条件，将这四个隶属度加起来，刚好等于1。这是因为（a + （1 - a）） \\* （b + （1 - b）） = a \\* b + ( 1 - a ) \\* b + a \\* ( 1 - b ) + ( 1 - a ) \\* ( 1 - b ) （下图）即一个十字相乘的概念。这个等式说明输出值的隶属度之和等于1（第三步求解的时候需要用到隶属度之和）。

因此，我们知道了输出值为ZO的隶属度和为 a \\* b + a \\* ( 1 - b ) + ( 1 - a ) \\* ( 1 - b ) ，输出值为NS的隶属度为 ( 1 - a ) \\* b 。

2.3 清晰化

对于输出值，我们同样采用给予隶属度的办法。例如，我们把输出值假设为[1000，1400]（即舵机的摆角值范围）的区间同样划分为八个部分，即7个隶属值NB,NM,NS,ZO,PS,PM,PB。根据上一步所得出的结论，我们就可以用隶属度乘以相应的隶属值算出输出值的解，即 （a \\* b + a \\* ( 1 - b ) + ( 1 - a ) \\* ( 1 - b ) ） \\* ZO + ( 1 - a ) \\* b \\* NS。到此为止，整个模糊过程就结束了。

3 模糊PID

我们已经知道了整个模糊的过程，但上述的过程还不够完美。因为我们的输出值只有一个输出，并没有实现PID。因此我们可以先对E和EC进行模糊化，然后分别对kp和ki和kd（PID的三个参数）进行求解，再套入公式。

一般的我们也可以只用kp，kd，不用ki。而模糊规则表一般的论文已经基本给出。因此带入算法之后我们的难度也只是在于调节kp，kd，和适当调节规则表。当然调节的难度会大于普通的PID，因为还要定kp，kd的输出范围，调得不好可能效果并没有普通的PID好。

4.部分解释

4.1对于部分论文所说的重心法解模糊，其实就是上述方法。公式如下。

式中μ（Zi） \\* Zi相当于文章上面的（a \\* b + a \\* ( 1 - b ) + ( 1 - a ) \\* ( 1 - b ) ） \\* ZO + ( 1 - a ) \\* b \\* NS，即隶属度乘以隶属度值之和，而μ（Zi）之和就是输出值的隶属度之和，我们已经证明它是等于1的

PS:模糊控制表在相关书籍中都有，都是前辈的经验，一般的无需修改即可，不过如果自己要配自己的数据也可以自己配，逻辑关系理清楚就可以了，反正我自己理来理去还是挺锻炼对pid三个变量的理解的，当然不止pid,模糊控制也可以单独使用，很灵活的，重点就是各个参数范围确定，这是影响模糊控制最重要的因素。

2.转自 https://blog.csdn.net/akunainiannian/article/details/41130347

matlab版本：matlab2010b
第一步：利用matlab模糊控制工具箱设计模糊控制器。

1、在matlab命令窗口中输入 fuzzy ，产生如下窗口。

2、确定模糊控制器结构，即根据具体的系统确定输入、输出量。

这里我们可以选取标准的二维控制结构，即输入为误差e和误差变化ec，输出为控制量u。输入变量的添加通过 Edit -> Add Variable -> Input 实现。

3、语言值及隶属函数的确定。

首先我们要确定描述输入输出变量语言值的模糊子集，如NB，NM，NS，ZE，PS，PM，PB，并设置输入输出变量的论域，例如我们设置误差E、误差变化EC的论域为[-6 6]，控制量U的论域为[-10 10]；然后为模糊语言变量选取相应的隶属度函数。通过 Edit -> Membership Functions 打开隶属度函数编辑器，然后分别对输入输出变量定义论域范围，添加隶属函数，以E为例，设置论域范围为[-6 6]，添加隶属函数的个数为7。（注：隶属度函数编辑器初始时已为每个变量定义了3个隶属函数，再通过 Edit -> Add MFs 添加隶属函数时，个数选择4即可）

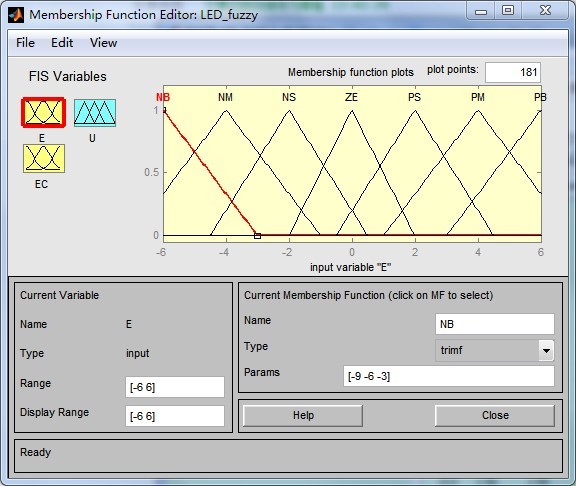
4、模糊控制规则的制定。

对于我们这个二维控制结构以及相应的输入模糊集，我们可以制定49条模糊控制规则。

5、解模糊。

模糊控制器的输出量是一个模糊集合，通过解模糊化方法判决出一个确切的精确量，解模糊化方法很多，我们这里选取重心法。

6、保存建立的模糊控制器。

File -> Export -> To File，文件名为 fuzzy_control。

第二步：建立Simulink模型。

1、在matlab命令窗口中输入simulink，产生如下窗口。

2、新建模糊控制器模型，样式如下。

3、在matlab命令窗口下输入 fuzzy = readfis(‘fuzzy_control’) ，将之前建立的模糊控制器加载到工作空间，并将Fuzzy Logic Contrtoller的参数设置为fuzzy。

4、保存该模型，命名为 fuzzy_model

第三步：系统测试界面的设置。

1、通过 Tools -> System Test -> Launch System Test 进入系统测试界面。

2、添加测试模型。

鼠标选中Main Test ，菜单栏 Insert -> Test Element -> Simulink ，选择第二步中建立的模型 fuzzy_model 。

3、变量定义。

在Test Vectors 项里定义两个测试向量，变量名分别为 input1、input2，input1 = [-6:1:6]， input2 = [-6:1:6]；在Test Variables 里定义测试变量，变量名为output。

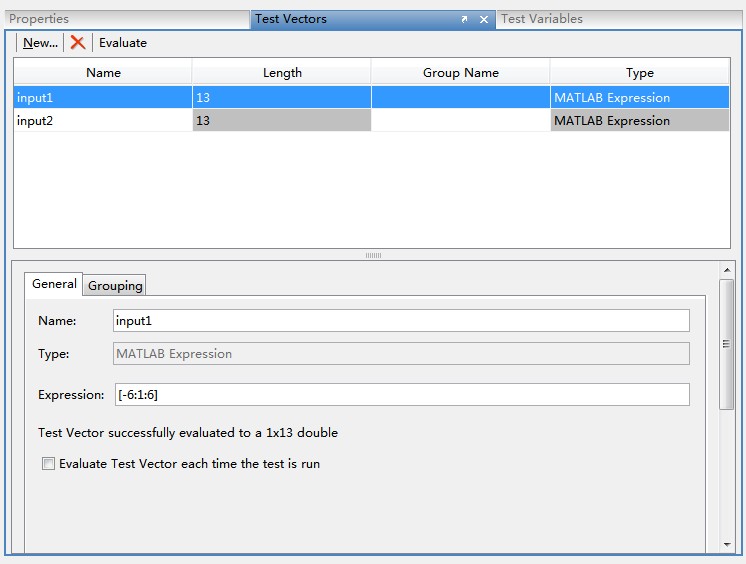
4、变量映射。

把测试向量input1、input2分别映射到模糊控制器的输入口 in1、in2，做为输入测试信号。把测试变量 output 映射到模糊控制器输出口out1。设置后的界面如下：

输入测试向量到模糊模型输入口映射：

模糊控制器输出保存映射：

5、测试数据保存。

在测试界面点Save Results项，设置如下：

6、运行测试，注意在Main Test(169 Iterations）(169次迭代，运算代价),等待测试结束。

第四步：模糊控制查询表的生成

1、系统测试结果保存在 stresults.ResultsDataSet.output 中，为169*1 cell的单元数组。（注：单元cell为 [n*1 double] 结构，表示系统被测试了n次）。

2、在matlab命令窗口下输入 test_data = stresults.ResultsDataSet.output ，将测试结果另存在变量 test_data 中。

3、测试结果格式转换。

由于所建的二维查询表为13行13列，所需的数据应该为13*13 double数组，但因为test_data为 169*1 cell 的单元数组，无法直接作为表格数据输入，因此需先进行格式转换。

在matlab命令窗口下输入 table_data = Cell2Array( test_data , 1 , 13 , 13 ) ，调用Cell2Array函数，取每个单元数组中的第一行元素，即第一次测试数据，返回结果保存在 table_data 中。

源码如下：

4、新建二维查询表模型，样式如下：

5、点开二维查询表进行如下设置：

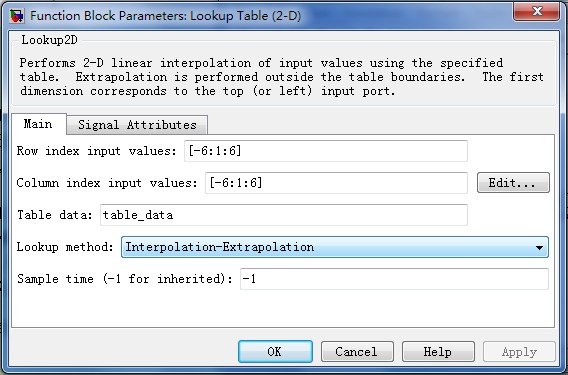
6、点 Edit 按钮，即可查看所生成的表格。

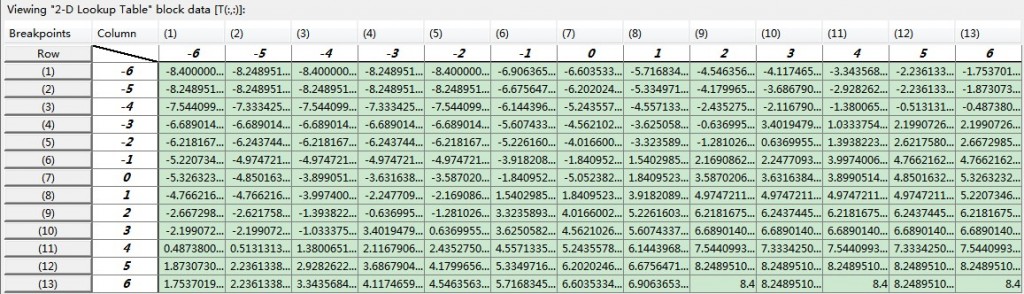
PS：以上两篇就是我基本完成的教程了，matlab因为自己不怎么熟，所以折腾了挺久的，基本就是从matlab什么都不懂到可以完成这个仿真，然后我也把新手可能出现的一些问题讲讲吧。

看了第一篇之后到matlab模糊控制器的设置保存应该问题不大，之后就是建立仿真模型，因为从来没用过所以一窍不通，我的版本是2016b,界面也和上面的有些不同，可是吃了点苦头，所以以下就是给新手看看的，不要笑我教的简单哈

首先，simulink界面不同，我的是新版的

是这样的界面，刚开始一脸懵逼不知道怎么建立仿真模型

之后随便点一个建立一个新的就好

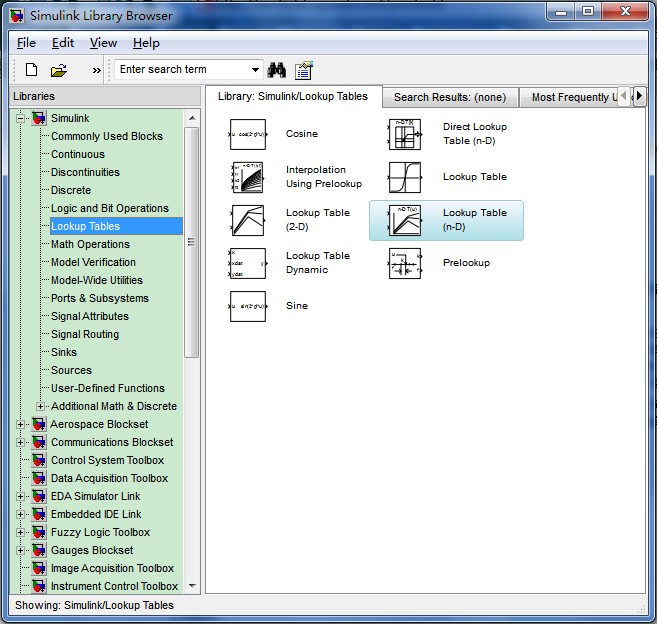
这个界面之后点那个Library Browser,里面有需要的元素，你就按上面那个图把元素都复制过来就好

注意那个fuzzy的图标，改变输出的个数是双击它有选项，我当初找了半天硬是找不到，，

把该加的东西都放进去，连接好

然后在matlab命令行里把之前保存的模型读取出来

用readfis命令把之前保存的数据赋给变量fuzzy，模型名字你们取得是什么就写什么

之后在仿真fuzzy图形上双击，把参数设成fuzzy，就是上面的步骤

最后就是test了，很坑啊，matlab2016a之后的版本就没有那个功能了，所以得用下别人的软件来做最后的测试，之后就看着慢慢设置就好，我只做到了测试运行那一步，因为参数还要调整所以就没到之后导表

大概就这么多了，其实都是给新手讲的，也想给自己留着复习复习，还有感谢各位在csdn里留下的各种学习资料，谢谢