线性规划和约束满足问题的思考

Posted 2022-12-05 willwillie

本文写给对线性规划和约束满足问题的使用有困惑的朋友，如果你曾经在这方面存在一些疑问，这篇文章对你来说就再适合不过了，如果有对线性规划的解法感兴趣，那么也推荐你看一看我的思考~
*注：之前一直以为约束满足问题和线性规划问题是一样的，才发现其实不是这样的，仔细想想我之前的理解原来存在着那么大的误会。虽然也不能说他们完全不一样，因为基本上模型一样，具体的算法却是不一样的。为什么呢，因为这两类问题的目标不一样。约束满足问题，一般用于求解满足约束问题的所有解，所以使用搜索算法比较好，而线性规划或者整数规划问题，一般用于找出满足某个条件的最优解，一般使用单纯形法和分支定界法等。

约束满足问题

约束满足问题的定义：

约束满足问题（CSP）是一类数学问题，它的定义为一组状态必须满足于若干约束或限制的对象(object)。 CSPs表示的是问题中的实体，有限数量、同类型的约束加之于变量之上, 这类问题通过 约束满足 方法解决。CSPs是人工智能和运筹学的热门主题, 这是因为它们公式中的规律提供了一个分析和解决很多不相关问题的共同基础。 CSPs通常表现出高复杂性, 需要结合启发式搜索 和联合搜索 方法来在合理的时间内解决问题。 —wiki

TSP旅行商问题在很长一段时间内的研究都被建模为约束满足问题，很多解法都是基于启发式搜索的。

CSPs的解决方案
确定域上的约束满足问题通常是利用搜索方法来解决的。 最常用的技术是回溯、约束传递，以及局部搜索的变种，这些算法也能很有效的解决则一类问题。

软件世界里是有很多用来解决约束满足问题的软件的，比如java库提供的开源choco引擎：

Choco is a Free Open-Source Java library dedicated to Constraint Programming.The user models its problem in a declarative way by stating the set of constraints that need to be satisfied in every solution.Then, the problem is solved by alternating constraint filtering algorithms with a search mechanism.

由上面的讲解可见choco的解题思路是基于搜索算法的。Choco是一个解决约束满足问题（CSP：Constraint Satisfaction Problems）的java库，用于解决约束规划。Choco的历史要追朔到1999年，一个叫做OCRE的项目，当时还是C++编程。在2003年，choco有一个主要的修改，被编进了Java编程语言，这是为了保证更好的可移植性。在2008年，choco又向前迈进了一大步，因为choco项目雇了全职的开发者来开发它，新的改进大大提高了性能，并且对用户也更加友好了。
Choco v2就得到了极大的利用，不仅仅是教学研究，还有很多公司使用了choco来解决实际问题。解决问题的方法是基于约束规划的技巧，我们只要按照规则建模编程，choco就可以给出解答。Choco不仅可以用于教学研究，对于生产来说，也是很便捷的，易于和语言软件集成。

问题的解答用的并不是单纯形法和分支定界法 而是https://en.wikipedia.org/wiki/Aho%E2%80%93Corasick_algorithm；https://en.wikipedia.org/wiki/Local_consistency#Arc_consistency

线性规划问题

在数学中，线性规划（Linear Programming，简称LP）特指目标函数和约束条件皆为线性的最优化问题。
线性规划是最优化问题中的一个重要领域。在作业研究中所面临的许多实际问题都可以用线性规划来处理，特别是某些特殊情况，例如：网络流、多商品流量等问题，都被认为非常重要。目前已有大量针对线性规划算法的研究。很多最优化问题算法都可以分解为线性规划子问题，然后逐一求解。在线性规划的历史发展过程中所衍伸出的诸多概念，建立了最优化理论的核心思维，例如“对偶”、“分解”、“凸集”的重要性及其一般化等。在微观经济学和商业管理领域中，线性规划亦被大量应用于例如降低生产过程的成本等手段，最终提升产值与营收。乔治·丹齐格被认为是线性规划之父。—wiki

和约束满足问题不同，线性规划问题必须要有目标函数，而通过前面约束满足问题的定义可以看出，约束满足问题的目标函数是可有可不有的。
线性规划问题被大量利用，数学家们前仆后继在这个问题上付出了大量的心血。了解线性规划问题求解是需要比较深厚的数学功底（线性代数）的，而问题的建模则最好需要了解些运筹学的知识。

模型
约束规划，也就是线性规划，线性规划模型的一般形式为：
一个目标函数 n个变量，m个约束条件，最后求解一组变量的值
其一般形式为：
目标函数：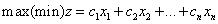

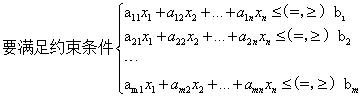
例子:
在那本讲TST的书里面，引入了一个产品生产例子，这个和我的分配问题建模将会很类似：
假设生产A、B、C三种产品，他们的量分别使用A、B、C表示。生产产品需要输入两种原料，假设为N和S,库存量分别为100和200；产品A需要3个单位N和4个单位S, 产品B需要3个单位N和2个单位S, 产品C需要1个单位N和8个单位S。每单位产品A盈利10，每单位产品B盈利5，每单位产品C盈利15。问题是，怎样安排生产产品，才能在不超过原料库存量的情况下赚到最多的钱？
=》对这道题建模，得到线性规划模型如下：

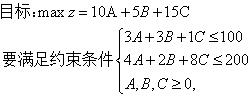
这个题目很简单，或许你靠心算就能得到正确的答案。但是实际生产问题复杂的多，变量和约束条件的数目可能成千上万，靠心算完全算不出来。

一般解法：simplex algorithm
1948年，Dantzig公布了线性模型和单纯形算法。这个算法的主要思想是：通过换主元操作把一部字典变成另一部字典，每一步都希望增加目标函数的值。那么具体要怎么做呢(假设你已经对线性规划相关的知识烂熟于心)，simplex method求解步骤如下，

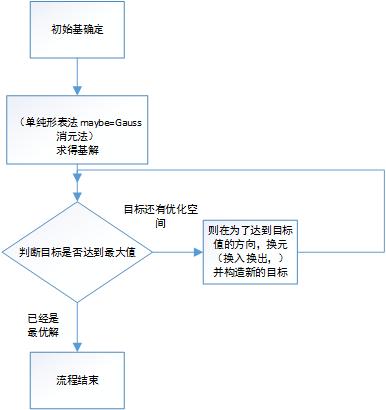
在确定了初始基（B=(P1,P2,…,Pm)）后,相应的变量是基变量，令非基变量的值都为0，利用gauss消元法，可以得到一个解X。
那么怎么判断目标是否达到了最大值呢？通过将目标函数表示成非基变量的线性表达式，通过目标函数的表达式：
比如z=2x1+3x2,很显然当x1=0且x2=0的时候z是没有达到最大值的.

换元，换入换出的方法：
对于换入的变量就是将能够最大限度引起目标变大的值换入（作为基变量）；
对于换出的变量是从原来的基变量中选择一个作为换出变量。保证在使得换入的那个变量尽量大（这样会使得目标值最大）的情况下，这些基变量都是非负的，那么可以确定这个换入变量的值，比如上图中的x2=3,也就能够算出这些基变量的值x5=0,将基变量为0的变量最为非基变量（也就是换出变量）。
然后再将目标函数的值表达为非基变量的线性表达式，重复前面的表达式就ok了。

关于单纯形更深入的理解
（之前我一直想从数学意义上证明，这是最优解，才发现这是不现实的也没有必要，对于线性规划问题，想的更多的应该是为什么这个方法可以求得最优解?为什么这个方法这么高效，高明在什么地方？）
我们可以看到，对于二维的问题，通过图解法我们还可以给出解答，但是对于高维的线性规划问题，图解法已经失去了作用。这个时候遇到这种问题，脑子里冒出的第一个想法就是用搜索法，在线性空间里一个点一个点的去搜索，看哪些能满足约束条件，然后算目标值，一步步比较目标值，然后这却不是好办法。
单纯形法的做法是通过给不等式添加松弛变量将线性规划问题化为标准形式，选定一组基，令非基变量全为0，则求出一组基变量的解，这样得到的解当然不一定是最优的，可以将目标函数表示为非基变量的表达式，然后判别目标函数是否达到了最优（变量前面的参数<=0），如果不是，就想办法让目标能够更优。想什么办法呢?既然基变量不是唯一的，如果变量的参数大于0，就选择那个最大的参数的变量作为换入变量（至少换入变量的值>=0）,再从原来的基变量中选择一个作为换出变量（这个时候要使得换入变量的值最大，此时基变量都可以酸的一个值（将值最小的基变量换出应该可以？）），这样就会求得一组解，然后得到又一个目标表达式（此时目标表达式的值必然已经增大了，但是表示的方法变了（再一次判断是否达到了最大值）），直到最大为止。
其实通过给不等式添加松弛变量将线性规划问题转化为更加高维的空间问题，选定基变量的过程，将高维空间映射到更加低维的空间，这样可以求得一个目标值，然后判断目标值是否有增长的空间，如果有，就换一组基变量，将问题的高维空间映射到另外一个低维空间，然后再次判断目标值是否达到了最大，没有的话，继续将高维空间转化成新的低维空间，直到目标值达到最大为止。
可以看到，单纯形法非常的精妙又高明（而且数学上线性代数对这个方法也产生了很大的助益），虽然第一个产生的解是比较随机的，但是每一步往下推目标都可以产生一个很大的跳跃最终稳定于最优解（或者终止于无解），反正目前还没有比这更精妙的方法产生。
使用空间变换的算法还有PageRank算法，不过PageRank不会变换线性空间的维度，利用矩阵乘法和马尔科夫链定理（PageRank值在转移过程中变化规律是完全可以用马尔科夫的状态转移来进行表征的，两者本质属于同一个问题。则当PageRank值收敛时，即为马尔可科夫链达到平衡分布（《随机分布》）），最终使得所有页面的PR值达到稳定（这样的过程和单纯形法的过程就是很类似的）。

整数规划/分支定界法
分枝界限法(Branch and Bound Method)
在前面讨论的线性规划问题中，对于某些具体问题，常常要求解必须是整数。比如机器的台数，完成工作的人数和装货的车数。这就是整数规划，目前，整数规划的求解大部分都使用分支定界法，分支定界法是在单纯形法的基础上定整数界，可以参考博文。
虽然分支定界法内含搜索的性质，但是CSP问题使用的搜索算法和分支定界法还是有明显的不一样的： 回溯法深度优先搜索堆栈活结点的所有可行子结点被遍历后才被从栈中弹出找出满足约束条件的所有解；分支限界法广度优先或最小消耗优先搜索队列、优先队列每个结点只有一次成为活结点的机会找出满足约束条件的一个解或特定意义下的最优解。

割平面法

割平面法的基础仍然是用解线性规划的方法去解整数规划问题。首先不考虑变量为整数这一约束条件。但增加线性约束条件(用几何术语，称为割平面)使得从原可行解域中切割掉一部分，这部分只包含非整数解，但没有切割掉任何整数可行解。因此，采用割平面法的关键是如何找到割平面约束方程，使切割后最终得到这样的可行解域，它的一个有整数坐标的极点恰好就是问题的最优

很多NP难题，通过线性规划建模可以给出比较赞的解答，比如TSP问题，虽然也可以使用搜索算法和启发式算法。

C++开源软件 glpk

the GLPK (GNU Linear Programming Kit) package is intended for solving
large-scale linear programming (LP), mixed integer programming (MIP),
and other related problems. It is a set of routines written in ANSI C and organized in the form of a callable library.
The GLPK package includes the following main components:
primal and dual simplex methods primal-dual interior-point method
branch-and-cut method translator for GNU MathProg application program
interface (API) stand-alone LP/MIP solver

glpk的算法基本上采用了单纯形法，和分支限界法和割平面法的结合。

复杂度分析
对于整数规划问题，计算的复杂度如何？假如采用暴力枚举的方案，那么计算的时间复杂度是n的阶乘或者M的n次方。
那么对于刚刚前面提到的分支定界法呢？虽然单纯形法和分支定界法看起来很巧妙，对于计算比较简单的约束规划可能确实比较有效率；但是在数学的世界里，目前还没法保证simplex algorithm是多项式时间的，也就更没法保证分支定界法是有多项式时间的。在约束变量和条件成千上万的时候，用这些方法计算问题也是很困难的。
目前来看，整数规划问题属于NP问题，求解困难。但是计算机的性能日益增加，当年可能需要一台机器工作十年算出的整数规划（2000个约束），现在一台性能较好的机器在比较短的时间内（比如几个小时）就能够算出来了。

取舍

在现实中要解决问题，不可能这些复杂的算法都自己造轮子，难度太大。最好的做法是先建模，然后使用已有的软件，比如约束和规划问题，使用choco或glpk等。然而虽然模型相同，两种引擎的算法却不同，那么怎么取舍呢？也就是说什么问题适合搜索的算法，什么问题适合用线性规划的算法？ 有一些问题其实无论用回溯法还是分支限界法都可以得到很好的解决，但是另外一些则不然。

参考文档

1.《迷茫的旅行商—一个无处不在的计算机算法问题》，美，William.J.Cook 2.《运筹学.第三版》，清华大学出版社 3. http://choco.sourceforge.net/benchmark/report.html（choco性能报告） 4. http://choco-solver.org/ 5.choco:an open source Java Constraint Programming Library 6. https://en.wikipedia.org/wiki/Constraint_programming

---

更新中（部分观点还在整理中）