后缀数组总结

Posted 2022-12-05 xuejye

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了后缀数组总结相关的知识，希望对你有一定的参考价值。

后缀数组求不可重叠最长重复子串

题意：有N(1 <= N <=20000)个音符的序列来表示一首乐曲，每个音符都是1..88范围内的整数，现在要找一个重复的主题。“主题”是整个音符序列的一个子串，它需要满足如下条件：

1.长度至少为5个音符。

2.在乐曲中重复出现。(可能经过转调，“转调”的意思是主题序列中每个音符都被加上或减去了同一个整数值)

3.重复出现的同一主题不能有公共部分。

这是论文里一道题，那么我们通过进行二分来求论文里的k值，求出height[i]大于k的时候，然后求出这个区间里面起始位置最大的差值，要求差值也要大于k，这样才保证没有重叠，这是因为height里的都是已经按照字典序排好的了

Sample Input

30
25 27 30 34 39 45 52 60 69 79 69 60 52 45 39 34 30 26 22 18
82 78 74 70 66 67 64 60 65 80
0

Sample Output

#include <stdio.h>
#include <algorithm>
#include <iostream>
using namespace std;
#define maxn 22222
int n;
int s[maxn],c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn];
void SA(int m)

    for(int i=0;i<m;i++)
        c[i]=0;
    for(int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(int k=1;k<=n;k<<=1)
    
        int p=0;
        for(int i=n-k;i<n;i++)
            y[p++]=i;
        for(int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
//        for(int i=0;i<n;i++)
//            cout << y[i] << " " ;
//        cout << endl;
        for(int i=0;i<m;i++)
            c[i]=0;
        for(int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
//        for(int i=0;i<n;i++)
//            cout << sa[i] << " " ;
//        cout << endl;
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
//        for(int i=0;i<n;i++)
//            cout <<x[i] <<" " ;
//        cout << endl;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    int k=0;
    for(int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(int i=0;i<n;i++)
    
        if(k)
            k--;
        int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    
//    for(int i=0;i<n;i++)
//        cout << height[i] <<" ";
//    cout <<endl;

int check(int len)

    int maxx=0,minn=maxn;
    for(int i=2;i<=n;i++)
    
        if(height[i]>=len)
        
            maxx=max(maxx,sa[i]);
            minn=min(minn,sa[i]);
            if(maxx-minn>len)
                return 1;
        
        else
        
            maxx=sa[i];
            minn=sa[i];
        
    
    return 0;

int main()

    while(scanf("%d",&n)!=EOF&&n)
    
        int ans=0;
        int x;
        scanf("%d",&x);
        for(int i=1;i<n;i++)
        
            int mid;
            scanf("%d",&mid);
            s[i-1]=mid-x+100;
            x=mid;
        
        s[n-1]=0;
        SA(200);
        n--;
        getheight();
        int l=0;
        int r=n;
        while(l<=r)
        
            int mid=(l+r)>>1;
            if(check(mid))
            
                ans=mid;
                l=mid+1;
            
            else
                r=mid-1;
        
        if(ans<4)
            ans=-1;
        printf("%d\\n",ans+1);

可重叠的k次最长重复子串

题意：找出出现k次的可重叠的最长子串的长度

通过二分长度，然后分成若干组去寻找答案

Sample Input

Sample Output

#include <stdio.h>
#include <algorithm>
using namespace std;
#define maxn 22222
int n;
int s[maxn],c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn];
void SA(int m)

    for(int i=0;i<m;i++)
        c[i]=0;
    for(int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(int k=1;k<=n;k<<=1)
    
        int p=0;
        for(int i=n-k;i<n;i++)
            y[p++]=i;
        for(int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
//        for(int i=0;i<n;i++)
//            cout << y[i] << " " ;
//        cout << endl;
        for(int i=0;i<m;i++)
            c[i]=0;
        for(int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
//        for(int i=0;i<n;i++)
//            cout << sa[i] << " " ;
//        cout << endl;
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
//        for(int i=0;i<n;i++)
//            cout <<x[i] <<" " ;
//        cout << endl;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    int k=0;
    for(int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(int i=0;i<n;i++)
    
        if(k)
            k--;
        int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    
//    for(int i=0;i<n;i++)
//        cout << height[i] <<" ";
//    cout <<endl;

int check(int len,int k)

    int cnt=1;
    for(int i=2;i<=n;i++)
    
        if(height[i]>=len)
        
            cnt++;
            if(cnt>=k)
                return 1;
        
        else
            cnt=1;
    
    return 0;

int main()

    int k;
    int maxx=0;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++)
    
        scanf("%d",&s[i]);
        maxx=max(maxx,s[i]);
    
    s[n]=0;
    n++;
    SA(maxx+1);
    n--;
    getheight();
    int l=0;
    int r=n;
    int ans=0;
    while(l<=r)
    
        int mid=(l+r)>>1;
        if(check(mid,k))
        
            ans=mid;
            l=mid+1;
        
        else
            r=mid-1;
    
    printf("%d\\n",ans);

求不相同的子串个数

题意：给定一个字符串，求不相同的子串。
思路：每个子串一定是某个后缀的前缀，那么原问题等价于求所有后缀之间的不相同的前缀的个数。如果所有的后缀按照 suffix(sa[1]), suffix(sa[2]),
suffix(sa[3]), …… ,suffix(sa[n])的顺序计算，不难发现，对于每一次新加
进来的后缀 suffix(sa[k]),它将产生 n-sa[k]个新的前缀。但是其中有height[k]个是和前面的字符串的前缀是相同的。所以 suffix(sa[k])将“贡献”
出 n-sa[k]-height[k]个不同的子串。累加后便是原问题的答案。

Sample Input:
2
CCCCC
ABABA

Sample Output:
5
9

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
using namespace std;
#define maxn 55555
long long int  n;
char s[maxn];
long long int  c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn];
void SA(long long int  m)

    for(long long int  i=0;i<m;i++)
        c[i]=0;
    for(long long int  i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(long long int  i=1;i<m;i++)
        c[i]+=c[i-1];
    for(long long int  i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(long long int  k=1;k<=n;k<<=1)
    
        long long int  p=0;
        for(long long int  i=n-k;i<n;i++)
            y[p++]=i;
        for(long long int  i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
//        for(long long int  i=0;i<n;i++)
//            cout << y[i] << " " ;
//        cout << endl;
        for(long long int  i=0;i<m;i++)
            c[i]=0;
        for(long long int  i=0;i<n;i++)
            c[x[y[i]]]++;
        for(long long int  i=1;i<m;i++)
            c[i]+=c[i-1];
        for(long long int  i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
//        for(long long int  i=0;i<n;i++)
//            cout << sa[i] << " " ;
//        cout << endl;
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(long long int  i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
//        for(long long int  i=0;i<n;i++)
//            cout <<x[i] <<" " ;
//        cout << endl;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    long long int  k=0;
    for(long long int  i=0;i<=n;i++)
    
        rrank[sa[i]]=i;
        //cout << sa[i] << endl;
    
    for(long long int  i=0;i<n;i++)
    
        if(k)
            k--;
        long long int  j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        //cout << rrank[i] << " " << k <<endl;
        height[rrank[i]]=k;
    
//    for(long long int  i=0;i<n;i++)
//        cout << height[i] <<" ";
//    cout <<endl;

int  main()

    long long int  t;
    scanf("%lld",&t);
    while(t--)
    
        scanf("%s",s);
        n=strlen(s);
        n++;
        SA(300);
        n--;
        getheight();
        long long int  ans=n*(n+1)/2;
        for(long long int  i=2;i<=n;i++)
        
            //cout << height[i] <<endl;
            ans-=height[i];
        
        printf("%lld\\n",ans);

重复次数最多的连续重复子串

Sample Input

1
17
b
a
b
b
a
b
a
a
b
a
a
b
a
a
b
a
b

Sample Output

【题意】

给定一个字符串，求重复次数最多的连续重复子串

【类型】
后缀数组[重复次数最多的连续重复子串]
【分析】

本题是一道裸的后缀数组题

"重复次数最多的连续重复子串"解法(摘自罗穗骞的国家集训队论文):

先穷举长度L，然后求长度为L的子串最多能连续出现几次。首先连续出现1次是肯定可以的，所以这里只考虑至少2次的情况。假设在原字符串中连续出现2次，记这个子字符串为S，那么S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个。所以只须看字符r[L*i]和r[L*(i+1)]往前和
往后各能匹配到多远，记这个总长度为K，那么这里连续出现了K/L+1次。最后看最大值是多少。如图所示。

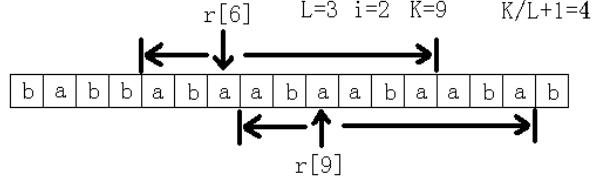
穷举长度L的时间是n，每次计算的时间是n/L。所以整个做法的时间复杂度是O(n/1+n/2+n/3+……+n/n)=O(nlogn)。

ps：基本思路在罗穗骞的论文里已经说得比较清楚了，而我在这里要提的是论文里比较模糊的部分

要提一提的总共有两点，第一点比较显而易见

“S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个”

由于当前S是有两个长度为L的连续重复子串拼接而成的，那意味着S[i]和S[i+L](0≤i<L)必定是一样的字符

而这两个字符位置相差L

而字符r[0],r[L],r[L*2],r[L*3],......中相邻两个的位置差均为L

“只须看字符r[L*i]和r[L*(i+1)]往前和往后各能匹配到多远”，对于往后能匹配到多远，这个直接根据最长公共前缀就能很容易得到，即上图中的后缀Suffix(6)和后缀Suffix(9)的最长公共前缀。而对于往前能匹配到多远，我们当然可以一开始就把字符串反过来拼在后面，这样也能根据最长公共前缀来看往前能匹配到多远，但这样效率就比较低了。

其实，当枚举的重复子串长度为i时，我们在枚举r[i*j]和r[i*(j+1)]的过程中，必然可以出现r[i*j]在第一个重复子串里，而r[i*(j+1)]在第二个重复子串里的这种情况，如果此时r[i*j]是第一个重复子串的首字符，这样直接用公共前缀k除以i并向下取整就可以得到最后结果。但如果r[i*j]如果不是首字符，这样算完之后结果就有可能偏小，因为r[i*j]前面可能还有少许字符也能看作是第一个重复子串里的。
于是，我们不妨先算一下，从r[i*j]开始，除匹配了k/i个重复子串，还剩余了几个字符，剩余的自然是k%i个字符。如果说r[i*j]的前面还有i-k%i个字符完成匹配的话，这样就相当于利用多余的字符还可以再匹配出一个重复子串，于是我们只要检查一下从r[i*j-(i-k%i)]和r[i*(j+1)-(i-k%i)]开始是否有i-k%i个字符能够完成匹配即可，也就是说去检查这两个后缀的最长公共前缀是否比i-k%i大即可。
当然如果公共前缀不比i-k%i小，自然就不比i小，因为后面的字符都是已经匹配上的，所以为了方便编写，程序里面就直接去看是否会比i小就可以了。

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
#define maxn 55555
int n;
char s[maxn];
int c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn],st[maxn][20];
void SA(int m)

    for(int i=0;i<m;i++)
        c[i]=0;
    for(int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(int k=1;k<=n;k<<=1)
    
        int p=0;
        for(int i=n-k;i<n;i++)
            y[p++]=i;
        for(int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
        for(int i=0;i<m;i++)
            c[i]=0;
        for(int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    int k=0;
    for(int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(int i=0;i<n;i++)
    
        if(k)
            k--;
        int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    

void ST()

    for(int i=1;i<=n;i++)
        st[i][0]=height[i];
    for(int j=1;j<=19;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);

int getmin(int x,int y)

    int l=rrank[x];
    int r=rrank[y];
    if(l>r)
        swap(l,r);
    l++;
    int k=log2(r-l+1);
    return min(st[l][k],st[r-(1<<k)+1][k]);

int main()

    int t;
    scanf("%d",&t);
    while(t--)
    
        scanf("%d",&n);
        for(int i=0;i<n;i++)
            scanf(" %c",&s[i]);
        s[n]=0;
        n++;
        SA(128);
        n--;
        getheight();
        ST();
        //cout << getmin(0,2) << endl;
        int ans=0;
        for(int i=1;i<=n;i++)
            for(int j=0;j+i<n;j+=i)
        
            int tmp=getmin(j,j+i);
            int k=j-(i-tmp%i);
            tmp/=i;
            if(k>=0&&getmin(k,k+i)>=i)
                tmp++;
            ans=max(ans,tmp+1);
        
        printf("%d\\n",ans);

重复次数最多的连续重复子串

题意：给定一个串，长度<=10^5，求它重复次数最多的连续重复子串（输出字典序最小的那个）。

例如ccabcabc，答案就是abcabc

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
#define maxn 111111
int n;
char s[maxn];
int c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn],st[maxn][20];
void SA(int m)

    for(int i=0;i<m;i++)
        c[i]=0;
    for(int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(int k=1;k<=n;k<<=1)
    
        int p=0;
        for(int i=n-k;i<n;i++)
            y[p++]=i;
        for(int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
        for(int i=0;i<m;i++)
            c[i]=0;
        for(int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    int k=0;
    for(int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(int i=0;i<n;i++)
    
        if(k)
            k--;
        int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    

void ST()

    for(int i=1;i<=n;i++)
        st[i][0]=height[i];
    for(int j=1;j<=19;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);

int getmin(int x,int y)

    int l=rrank[x];
    int r=rrank[y];
    if(l>r)
        swap(l,r);
    l++;
    int k=log2(r-l+1);
    return min(st[l][k],st[r-(1<<k)+1][k]);

int a[maxn];
int main()

    int cnt=1;
    while(scanf("%s",s)&&strcmp(s,"#"))
    
        n=strlen(s);
        s[n]=0;
        n++;
        SA(128);
        n--;
        getheight();
        ST();
        int ans=0;
        string ss;
        int len=0;
        for(int i=1;i<n;i++)
            for(int j=0;j+i<n;j+=i)
        
            int ttmp;
            int tmp=ttmp=getmin(j,j+i);
            int k=j-(i-tmp%i);
            int mid=j;
            tmp/=i;
            if(k>=0&&ttmp%i)
                if(getmin(k,k+i)>=ttmp)
                    
                        tmp++;
                        mid=k;

                    
            if(ans<tmp+1)
            
                ans=tmp+1;
                len=0;
                a[len++]=i;
            
            if(ans==tmp+1)
            
                a[len++]=i;
            
        
        int flag=0,pos;
        for(int i=1;i<=n&&!flag;i++)
            for(int j=0;j<=len;j++)
        
            int mid=a[j];
            if(getmin(sa[i],sa[i]+mid)>=(ans-1)*mid)
            
                flag=mid;
                pos=sa[i];
                break;
            
        
        //cout << pos << flag <<endl;
        for(int i=0;i<flag*ans;i++)
            ss+=s[pos+i];
        printf("Case %d: ",cnt++);
        //cout << ans << endl;
        cout << ss << endl;

两串字符中都出现过的最长子串

题意：给你两串字符，要你找出在这两串字符中都出现过的最长子串.........

思路：先用个分隔符将两个字符串连接起来，再用后缀数组求出height数组的值，找出一个height值最大并且i与i-1的sa值分别在两串字符中就好.....

Sample Input

yeshowmuchiloveyoumydearmotherreallyicannotbelieveit
yeaphowmuchiloveyoumydearmother

Sample Output

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
#define maxn 222222
int n;
int ansnum;
int s[maxn];
int c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn],st[maxn][20],col[111],vis[111];
int ans[maxn],re[maxn];
void SA(int m)

    for(int i=0;i<m;i++)
        c[i]=0;
    for(int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(int k=1;k<=n;k<<=1)
    
        int p=0;
        for(int i=n-k;i<n;i++)
            y[p++]=i;
        for(int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
        for(int i=0;i<m;i++)
            c[i]=0;
        for(int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    int k=0;
    for(int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(int i=0;i<n;i++)
    
        if(k)
            k--;
        int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    

void ST()

    for(int i=1;i<=n;i++)
        st[i][0]=height[i];
    for(int j=1;j<=19;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);

int getmin(int x,int y)

    int l=rrank[x];
    int r=rrank[y];
    if(l>r)
        swap(l,r);
    l++;
    int k=log2(r-l+1);
    return min(st[l][k],st[r-(1<<k)+1][k]);

int check ()

    int mid=0;
    for(int i=2;i<=n;i++)
    
        if(col[sa[i]]!=col[sa[i-1]])
            mid=max(mid,height[i]);
    
    return mid;

int a[maxn];
int main()

    char smid[maxn];
    n=0;
    for(int i=0;i<2;i++)
        
            scanf("%s",smid);
            int len=strlen(smid);
            for(int j=0;j<len;j++)
                
                    col[n]=i;
                    s[n++]=smid[j];
                
            s[n++]=129+i;
        
    s[n-1]=0;
    SA(300);
    n--;
    getheight();
    cout << check() <<endl;

求出长度不小于k的公共子串个数

题意：给定两个字符串 A 和 B ，求长度不小于 k 的公共子串的个数（可以相同）。

计算A的某个后缀与B的某个后缀的最长公共前缀长度，如果长度L大于k，则加上L-k+1组。

将两个字符串连接起来，中间用一个没有出现的字符分开。（这是一个神奇的做法）

然后通过height数组分组，某个组内的height都是大于等于k的，也就是任意两个后缀的最长公共前缀都至少为k。

扫描一遍，遇到一个B的后缀就与之前的A后缀进行统计，求出所有的满足的组数。但是这样的做法便是n^2的。

可以发现两个后缀的最长公共前缀为这一段的height值的最小值。

可以通过一个单调栈来维护一下，当前要入栈元素如果小于栈底元素，说明之后加入的B后缀与栈底的最长公共前缀是小于等于入栈的。这样就保证了单调栈内的height值是绝对递增的，逐渐合并，均摊可以达到o(n)的复杂度。

然后扫描两遍即可

Sample Input

2
aababaa
abaabaa
1
xx
xx
0

Sample Output

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
#define maxn 222222
long long int n;
long long int ansnum;
long long int s[maxn];
long long int c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn],st[maxn][20],col[111],vis[111];
long long int ans[maxn],re[maxn];
void SA(long long int m)

    for(long long int i=0;i<m;i++)
        c[i]=0;
    for(long long int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(long long int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(long long int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(long long int k=1;k<=n;k<<=1)
    
        long long int p=0;
        for(long long int i=n-k;i<n;i++)
            y[p++]=i;
        for(long long int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
        for(long long int i=0;i<m;i++)
            c[i]=0;
        for(long long int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(long long int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(long long int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(long long int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    long long int k=0;
    for(long long int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(long long int i=0;i<n;i++)
    
        if(k)
            k--;
        long long int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    

void ST()

    for(long long int i=1;i<=n;i++)
        st[i][0]=height[i];
    for(long long int j=1;j<=19;j++)
        for(long long int i=1;i+(1<<j)-1<=n;i++)
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);

long long int getmin(long long int x,long long int y)

    long long int l=rrank[x];
    long long int r=rrank[y];
    if(l>r)
        swap(l,r);
    l++;
    long long int k=log2(r-l+1);
    return min(st[l][k],st[r-(1<<k)+1][k]);

long long int sta[maxn];
long long int stb[maxn];
long long int checka(long long int k)

    long long int ss=0;
    long long int top=0;
    long long int ans=0;
    for(long long int i=2;i<=n;i++)
        if(height[i]>=k)
        
            long long int cnt=0;
            if(col[sa[i-1]]==0)
            
                cnt++;
                ss+=height[i]-k+1;
            
            while(top>0&&height[i]<=sta[top-1])
            
                top--;
                ss-=stb[top]*(sta[top]-height[i]);
                cnt+=stb[top];
            
            sta[top]=height[i];
            stb[top++]=cnt;
            if(col[sa[i]]==1)
                ans+=ss;
        
        else
        
            top=ss=0;
        
        return ans;

long long int checkb(long long int k)

    long long int ss=0;
    long long int top=0;
    long long int ans=0;
    for(long long int i=2;i<=n;i++)
        if(height[i]>=k)
        
            long long int cnt=0;
            if(col[sa[i-1]]==1)
            
                cnt++;
                ss+=height[i]-k+1;
            
            while(top>0&&height[i]<=sta[top-1])
            
                top--;
                ss-=stb[top]*(sta[top]-height[i]);
                cnt+=stb[top];
            
            sta[top]=height[i];
            stb[top++]=cnt;
            if(col[sa[i]]==0)
                ans+=ss;
        
        else
        
            top=ss=0;
        
    return ans;

char a[maxn];
int main()

    long long int k;
    while(scanf("%lld",&k)!=EOF&&k)
    
        scanf("%s",a);
        long long int lena;
        lena=strlen(a);
        for(long long int i=0;i<lena;i++)
        
            s[i]=a[i];
            col[i]=0;
        
        s[lena]='#';
        col[lena]=-1;
        scanf("%s",a);
        long long int lenb;
        lenb=strlen(a);
        for(long long int i=0;i<lenb;i++)
        
            s[lena+1+i]=a[i];
            col[lena+1+i]=1;
        
        s[lena+1+lenb]=0;
        n=lena+lenb+2;
        SA(200);
        n--;
        getheight();
        printf("%lld\\n",checka(k)+checkb(k));

出现在至少k个字符串中的最长子串

给定n个字符串，求出现在多于n/2个字符串中的最大长度的子串。

用朴素的搜索方法肯定不能满足时间要求。因此还是使用后缀数组。

首先把问题变成判定性问题，即长度为某个值的满足条件的子串是否存在。这样就可以使用二分来求解。

接着是把n个字符串用某个字符连接起来。计算出sa数组和height数组。对于每个需要判定的长度，对height数组进行分组，对每个分组分别进行统计，如果该分组中包含了多于n/2个原串，则满足条件。

本题要求把所有满足条件的子串全部打印出来，因此可以把判定过程中得到的最大长度的子串的起始位置存下来，最后打印出来就可以了。

3
abcdefg
bcdefgh
cdefghi
3
xxx
yyy
zzz
0

Sample Output

bcdefg
cdefgh

?

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
#define maxn 111111
int n;
int num,ansnum;
int s[maxn];
int c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn],st[maxn][20],col[111],vis[111];
int ans[maxn],re[maxn];
void SA(int m)

    for(int i=0;i<m;i++)
        c[i]=0;
    for(int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(int k=1;k<=n;k<<=1)
    
        int p=0;
        for(int i=n-k;i<n;i++)
            y[p++]=i;
        for(int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
        for(int i=0;i<m;i++)
            c[i]=0;
        for(int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    int k=0;
    for(int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(int i=0;i<n;i++)
    
        if(k)
            k--;
        int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    

void ST()

    for(int i=1;i<=n;i++)
        st[i][0]=height[i];
    for(int j=1;j<=19;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);

int getmin(int x,int y)

    int l=rrank[x];
    int r=rrank[y];
    if(l>r)
        swap(l,r);
    l++;
    int k=log2(r-l+1);
    return min(st[l][k],st[r-(1<<k)+1][k]);

int check (int len)

    //cout << len <<endl;
    int cnt=0;
    for(int i=2;i<=n;i++)
    
        //cout << height[i] << endl;
        if(height[i]<len)
        
            cnt=0;
            for(int j=0;j<111;j++)
                vis[j]=0;
        
        else
        
            if(!vis[col[sa[i]]])
            
                vis[col[sa[i]]]=1;
                cnt++;
            
            if(!vis[col[sa[i-1]]])
            
                vis[col[sa[i-1]]]=1;
                cnt++;
            
        if(cnt>num/2)
        return 1;
    

    return 0;


int a[maxn];
int main()

    int lineflag=0;
    while(scanf("%d",&num)!=EOF&&num)
    
        if(lineflag)
        
            cout << endl;
        
        lineflag=1;
        char smid[maxn];
        n=0;
        for(int i=0;i<num;i++)
            
                scanf("%s",smid);
                int len=strlen(smid);
                for(int j=0;j<len;j++)
                    
                        col[n]=i;
                        s[n++]=smid[j];
                    
                s[n++]=129+i;
            
        s[n-1]=0;
        SA(300);
        n--;
        getheight();
        int l=1;
        int r=maxn;
        ansnum=0;
        while(l<=r)
        
            int mid=(l+r)>>1;
            if(check(mid))
            
                ansnum=mid;
                l=mid+1;
            
            else
                r=mid-1;
        
        //cout << ansnum <<endl;
        if(ansnum==0)
        
            cout << "?" << endl;
            continue;
        
        for(int i=0;i<111;i++)
        
            vis[i]=0;
        
        int cnt=0;
        int flag=1;
        for(int i=2;i<=n;i++)
        

            if(height[i]<ansnum)
            
                for(int i=0;i<111;i++)
                    vis[i]=0;
                cnt=0;
                flag=1;
            
            else
            
                if(!vis[col[sa[i]]])
                
                    vis[col[sa[i]]]=1;
                    cnt++;
                
                if(!vis[col[sa[i-1]]])
                
                    vis[col[sa[i-1]]]=1;
                    cnt++;
                
                if(cnt>num/2&&flag)
                
                    for(int j=0;j<ansnum;j++)
                        printf("%c",s[sa[i]+j]);
                    cout <<endl;

                    flag=0;

最长公共子串

题意:给定n个字符串，求出现或反转后出现在每个字符串中的最长子串。

思路：先将每个字符串都反过来写一遍，中间用一个互不相同的

且没有出现在字符串中的字符隔开，再将n个字符串全部连起来，中间也是用一

个互不相同的且没有出现在字符串中的字符隔开，求后缀数组。然后二分答案，

再将后缀分组。判断的时候，要看是否有一组后缀在每个原来的字符串或反转后

的字符串中出现。

Sample Input

2
3
ABCD
BCDFF
BRCD
2
rose
orchid

Sample Output

2
2

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
#define maxn 222222
long long int n;
long long int ansnum;
long long int s[maxn];
long long int c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn],st[maxn][20],col[maxn],vis[111];
long long int ans[maxn],re[maxn];
void SA(long long int m)

    for(long long int i=0;i<m;i++)
        c[i]=0;
    for(long long int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(long long int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(long long int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(long long int k=1;k<=n;k<<=1)
    
        long long int p=0;
        for(long long int i=n-k;i<n;i++)
            y[p++]=i;
        for(long long int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
        for(long long int i=0;i<m;i++)
            c[i]=0;
        for(long long int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(long long int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(long long int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(long long int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    long long int k=0;
    for(long long int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(long long int i=0;i<n;i++)
    
        if(k)
            k--;
        long long int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    

void ST()

    for(long long int i=1;i<=n;i++)
        st[i][0]=height[i];
    for(long long int j=1;j<=19;j++)
        for(long long int i=1;i+(1<<j)-1<=n;i++)
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);

long long int getmin(long long int x,long long int y)

    long long int l=rrank[x];
    long long int r=rrank[y];
    if(l>r)
        swap(l,r);
    l++;
    long long int k=log2(r-l+1);
    return min(st[l][k],st[r-(1<<k)+1][k]);

int m;
int check(int len)

    //cout << len <<endl;
    int cnt=0;
    for(int i=2;i<=n;i++)
    
        if(height[i]>=len)
        
            if(!vis[col[sa[i]]])
            
                vis[col[sa[i]]]=1;
                cnt++;
            
            if(!vis[col[sa[i-1]]])
            
                vis[col[sa[i-1]]]=1;
                cnt++;
            
            if(cnt>=m)
                return 1;
        
        else
        
//            if(cnt>=m)
//                return 1;
            cnt=0;
            for(int i=0;i<111;i++)
                vis[i]=0;
        
    
//    if(cnt>=m)
//                return 1;
    return 0;

char ss[maxn];
int main()

    int T;
	scanf("%d",&T);
	while(T--)
	
		n=0;
		int p=0;
		scanf("%d",&m);
		for(int i=1;i<=m;i++)
		
			scanf("%s",ss);
		    int len=strlen(ss);
		    for(int j=0;j<len;j++)
            
                col[n]=i;
                s[n++]=ss[j];
            
            s[n++]=128+p++;
            for(int j=len-1;j>=0;j--)
            
                col[n]=i;
                s[n++]=ss[j];
            
            s[n++]=128+p++;
		
		s[n-1]=0;
		SA(600);
		n--;
		getheight();
        int l=1;
        int r=111;
        int ans=0;
        while(l<=r)
        
            int mid=(l+r)>>1;
            if(check(mid))
            
                ans=mid;
                l=mid+1;
            
            else
                r=mid-1;
        
        if(m==1)
            ans=strlen(ss);
        cout << ans <<endl;

所有前缀出现次数和

Sample Input

aaa
abab

Sample Output

6
6

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
#define maxn 222222
int n;
char s[maxn];
int c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn],st[maxn][20];
void SA(int m)

    for(int i=0;i<m;i++)
        c[i]=0;
    for(int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(int k=1;k<=n;k<<=1)
    
        int p=0;
        for(int i=n-k;i<n;i++)
            y[p++]=i;
        for(int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
        for(int i=0;i<m;i++)
            c[i]=0;
        for(int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    int k=0;
    for(int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(int i=0;i<n;i++)
    
        if(k)
            k--;
        int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    

void ST()

    for(int i=1;i<=n;i++)
        st[i][0]=height[i];
    for(int j=1;j<=19;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);

int getmin(int x,int y)

    int l=rrank[x];
    int r=rrank[y];
    if(l>r)
        swap(l,r);
    l++;
    int k=log2(r-l+1);
    return min(st[l][k],st[r-(1<<k)+1][k]);

int main()

    while(scanf("%s",s)!=EOF)
    
        n=strlen(s);
        s[n]=0;
        n++;
        SA(200);
        n--;
        getheight();
        ST();
        int ans=0;
        for(int i=1;i<n;i++)
        
            ans=(ans+getmin(0,i))%256;
        
        ans=(ans+n)%256;
        cout << ans << endl;

求最长公共前缀

题目的本质就是求输入的相邻的两个串的最长公共字串，有sa来解求得height数组，然后用rmq算法查询。

Sample Input

frcode
2
0 6
0 6
unitedstatesofamerica
3
0 6
0 12
0 21
myxophytamyxopodnabnabbednabbingnabit
6
0 9
9 16
16 19
19 25
25 32
32 37

Sample Output

14 12
42 31
43 40

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
#define maxn 111111
long long int n;
char s[maxn];
long long int c[maxn],sa[maxn],x[maxn],y[maxn],height[maxn],rrank[maxn],st[maxn][20];
void SA(long long int m)

    for(long long int i=0;i<m;i++)
        c[i]=0;
    for(long long int i=0;i<n;i++)
        c[x[i]=s[i]]++;
    for(long long int i=1;i<m;i++)
        c[i]+=c[i-1];
    for(long long int i=n-1;i>=0;i--)
        sa[--c[x[i]]]=i;
    for(long long int k=1;k<=n;k<<=1)
    
        long long int p=0;
        for(long long int i=n-k;i<n;i++)
            y[p++]=i;
        for(long long int i=0;i<n;i++)
            if(sa[i]>=k)
                y[p++]=sa[i]-k;
        for(long long int i=0;i<m;i++)
            c[i]=0;
        for(long long int i=0;i<n;i++)
            c[x[y[i]]]++;
        for(long long int i=1;i<m;i++)
            c[i]+=c[i-1];
        for(long long int i=n-1;i>=0;i--)
            sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(long long int i=1;i<n;i++)
            x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
        if(p>=n)
            break;
        m=p;
    

void getheight()

    long long int k=0;
    for(long long int i=0;i<=n;i++)
        rrank[sa[i]]=i;
    for(long long int i=0;i<n;i++)
    
        if(k)
            k--;
        long long int j=sa[rrank[i]-1];
        while(s[i+k]==s[j+k])
            k++;
        height[rrank[i]]=k;
    

void ST()

    for(long long int i=1;i<=n;i++)
        st[i][0]=height[i];
    for(long long int j=1;j<=19;j++)
        for(long long int i=1;i+(1<<j)-1<=n;i++)
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);

long long int getmin(long long int x,long long int y)

    long long int l=rrank[x];
    long long int r=rrank[y];
    if(l>r)
        swap(l,r);
    l++;
    long long int k=log2(r-l+1);
    return min(st[l][k],st[r-(1<<k)+1][k]);

int main()

    while(scanf("%s",s)!=EOF)
    
        n=strlen(s);
        s[n]=0;
        n++;
        SA(300);
        n--;
        getheight();
        ST();
        long long int t;
        scanf("%lld",&t);
        long long int ans1=0,ans2=0;
        long long int prel,prer;
        scanf("%lld%lld",&prel,&prer);
        ans1+=prer-prel+1;
        ans2+=prer-prel+3;
        t--;
        while(t--)
        
            long long int l,r;
            scanf("%lld%lld",&l,&r);
            ans1+=r-l+1;
            ans2+=r-l+3;
            long long int mid=min(getmin(prel,l),min(r-l,prer-prel));
            if(prel==l)
                mid=min(r-l,prer-prel);
            //cout << mid <<endl;
            ans2-=mid;
            while(mid>=10)
            
                ans2++;
                mid/=10;
            
            prel=l;
            prer=r;
        
        cout << ans1 << " " << ans2 << endl;

以上是关于后缀数组总结的主要内容，如果未能解决你的问题，请参考以下文章

POJ 1743-POJ - 3261~后缀数组关于最长字串问题

POJ-1743 Musial Theme(后缀数组 + 二分)(男人八题)

poj 1743 Musical Theme（最长重复子串后缀数组）

[poj 1743] Musical Theme 后缀数组 or hash

POJ-2774 后缀数组基础题