机器学习-6.朴素贝叶斯

Posted 2022-12-05 wyply115

1. 基础的概率知识

• 条件概率和联合概率
• 联合概率：包含多个条件，且所有条件同时成立的概率。

1. 记作：P( A , B ) = P(A)P(B)

• 条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率

1. 记作：P(A|B)
2. 特性：P(A1,A2|B) = P(A1|B)P(A2|B)
3. 公式成立条件：A1和A2两个事件或特征相互独立，不会互相影响的前提下。

• 全概率公式：
  如果事件组B1，B2，… 满足
  1.B1，B2…两两互斥，即 Bi ∩ Bj = ∅ ，i≠j ， i,j=1，2，…，且P(Bi)>0,i=1,2,…;
  2.B1∪B2∪…=Ω ，则称事件组 B1,B2,…是样本空间Ω的一个划分
  设 B1,B2,…是样本空间Ω的一个划分，A为任一事件，则：
  $$P(A)=\sum _{i=1}^{n}P(B_i)P(A|B_i)$$
• 举例：
  有样本如下：
  
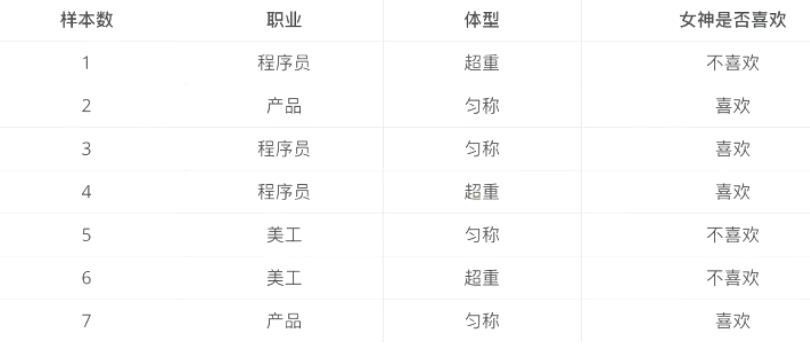
  求以下几个问题的概率：

6. 女神喜欢的概率？
7. 职业是程序员并且体型匀称的概率？
8. 在女神喜欢的条件下，职业是程序员的概率？
9. 在女神喜欢的条件下，职业是产品，体重是超重的概率？
   解答：第一题，4/7； 第二题：p(程序员，匀称）= (3/7) * (4/7) = 12/49 ；第三题：2/4=1/2；第四题：p(产品，超重 | 女神喜欢) = p(产品 | 女神喜欢)p(超重 | 女神喜欢) = (1/2) * (1/4) = 1/8

2. 朴素贝叶斯

• 贝叶斯公式：
  $$P(C|W)=\frac{P(W|C)P(C)}{P(W)}$$
• 注：w为给定文档的特征值（频数统计等），C为文档类别
• 公示可以理解为：
  $$P(C|F1,F2...)=\frac{P(F1,F2...|C)P(C)}{P(F1,F2...)}$$
• 注：其中C可以是不同的类别。

1. P( C )：每个文档类别的概率（某文档类别数量/总文档数量）
2. P(W|C)：给定类别下特征（被预测文档中出现的词）的概率。
   (1). 计算方法：P(F1|C) = Ni/N
   (2). Ni为该F1词在C类别所有文档中出现的次数
   (3). N为所属类别C下的文档所有词出现的次数和
3. P(F1,F2…)：预测文档中每个词的概率

• 理论推导：
  根据贝叶斯定理和朴素（条件独立）的假设可知道：对一个分类问题，给定样本特征x（假设特征向量维度为m），样本属于类别y的概率是 ：
  $$p(y|x)=\frac{p(x|y)p(y)}{p(x)}$$
  由于条件独立，可根据全概率公示，和条件概率的特性展开得：
  $$p(y=c_k|x)=\frac{{\prod }_{i=1}^{m}p(x^i|y=c_k)p(y=c_k)}{{\sum }_{k}p(y=c_k){\prod }_{i=1}^{m}p(x^i|y=c_k)}$$
  则朴素贝叶斯分类器可表述为：
  $$f(x)=argma{x}_{y_k}p(y=c_k|x)=argma{x}_{y_k}\frac{{\prod }_{i=1}^{m}p(x^i|y=c_k)p(y=c_k)}{{\sum }_{k}p(y=c_k){\prod }_{i=1}^{m}p(x^i|y=c_k)}$$
  对于所有的yk，由全加符号知道，分母的值都是一样的。因此朴素贝叶斯分类器最终可表示为：
  $$f(x)=argma{x}_{y_k}p(y=c_k|x)=argma{x}_{y_k}\prod _{i=1}^{m}p(x^i|y=c_k)p(y=c_k)$$
• 示例：
  
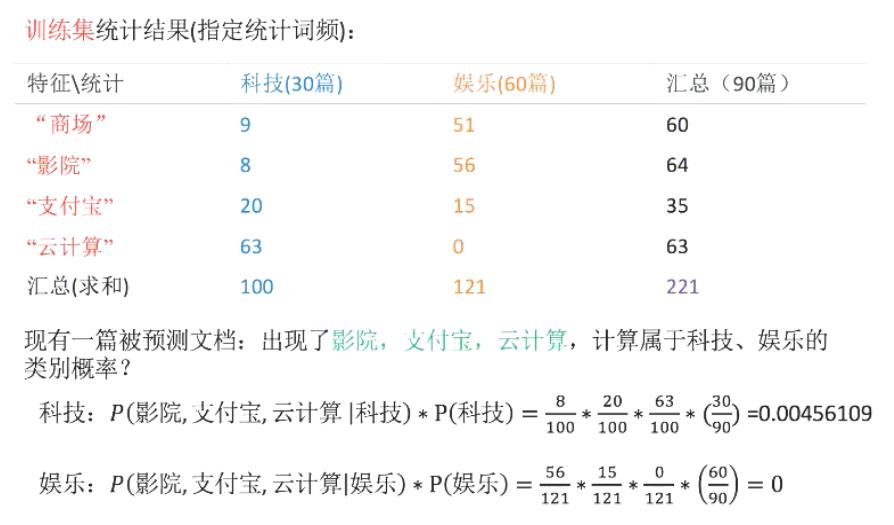
• 如上图，娱乐类计算结果为0，这样肯定是不合适的，因此引出拉普拉斯平滑系数。
• 拉普拉斯平滑系数：
  $$P(F1|C)=\frac{Ni+a}{N+am}$$
• a为指定的系数，一般为1，m为训练文档中统计出的特征词个数。
  假设我们设定a=1则：科技=(8+1)/(100+1) * (20+1)/(100+1) + (63+1)/(100+1) + 30/90 ；娱乐类同理，不再赘述。
• 朴素贝叶斯算法一般应用于对文章分类。
• API：sklearn.naive_bayes.MultinomialNB
• 示例：sklearn.dataset中获取新闻原始数据，对其分割数据集并进行预测分类。

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split


def naviebayes():
    '''
    朴素贝叶斯进行文本分类
    :return: None
    '''

    # 1.获取原始数据
    news = fetch_20newsgroups(subset="all")

    # 2.进行数据分割
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)

    # 3.特征抽取
    tf = TfidfVectorizer()
    #   以训练集当中的词的列表进行每篇文章的重要性统计
    x_train = tf.fit_transform(x_train)
    # print(tf.get_feature_names())
    #   以训练集的特征对测试集进行重要性统计
    x_test = tf.transform(x_test)

    # 4.进行朴素贝叶斯算法预测
    mlt = MultinomialNB(alpha=1.0)
    mlt.fit(x_train以上是关于机器学习-6.朴素贝叶斯的主要内容，如果未能解决你的问题，请参考以下文章
 
 机器学习--朴素贝叶斯分类，以及拉普拉斯校准
 机器学习面试题——朴素贝叶斯
 R语言机器学习 | 6 朴素贝叶斯
 机器学习实战教程：朴素贝叶斯实战篇之新浪新闻分类
 机器学习-6.朴素贝叶斯
 机器学习—朴素贝叶斯