Given \\(N\\) data samples in \\(n\\) dimensional space, i.e., \\(Y \\in R^{n\\times N}\\), the task is to compute the dictionary \\(D\\in R^{n\\times K}\\) and sparse component \\(X\\in R^{K\\times N}\\). Using the Frobenius norm, the task is summarized as the following optimization problem:
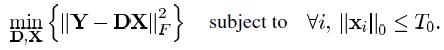
which is equivalent to
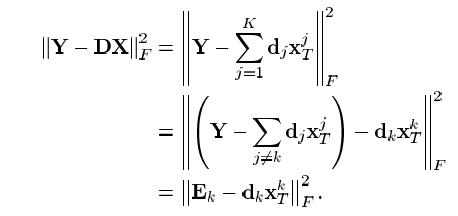
[Attention]
(1) If our aim is just the minimization of the first line shown above, the explicit solution is just the SVD of \\(Y\\), from which we can obtain \\(d_j\\) and \\(x_T^j (j=1,\\cdots,K)\\). However this will not lead to a sparse \\(x_T^j\\).
(2) The idea here is to use the last line incremently, i.e., from \\(k=1\\) to \\(K\\). When optimizing \\(d_k\\) and \\(x^k_T\\), we fix other columns of \\(D\\) and rows of \\(X\\). In this way, we elminate the summation in the first line. Thereby, we can further apply the following sparse-holding technique.
(3) Direct using SVD of \\(E_k\\) to obtain \\(d_k\\) and \\(x^k\\) will definitely destroy the existing sparsity of \\(x^k\\), thus is unfavorable. A remedy is to only consider the nonzero element of \\(x^k\\), this is equivalent to a selection matrix defined by
\\(\\Omega_k\\), the \\(k\\) here refer to the recursive procedure.
The effect of \\(\\Omega_k\\) to \\(x_k\\) is just the selection of nonzero elements of \\(x^k\\). For example, if \\(x=[1, 0, 2, 0, 3]\\), then \\(\\Omega=[e_1,e_3,e_4]\\in R^{5\\times 3}\\). So we can check that \\(x\\Omega=[1,2,3]\\).
So instead of application of SVD to \\(E_k\\), in \\(k-SVD\\) we apply SVD to \\(E_k^R:=E_k\\Omega_k\\). That is we optimize
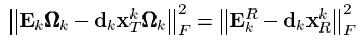
and this time it can be done directly via SVD. We define the solution for \\(d_k\\) as the first column of \\(U\\) and the coefficient vector \\(x_R^k\\) as the first column of \\(V\\) multiplied by \\(\\sigma(1,1)\\).
[Attention]
(1) There is a mistake in equation (22) in the original paper. The index \\(i\\) should in \\(1\\leq i\\leq N\\) rather than \\(K\\).
(2) Also when updating \\(d_2\\) and \\(x^2\\), we use the updated \\(d_1\\) and \\(x^1\\). That is to say, K-SVD works in a manner similar to G-S iteration.
(3) The original paper also says that you can also work in a parallel manner. That is to say update \\(d_2\\) and \\(x^2\\) using the same \\(X\\). But my question is how to do with \\(d_1\\)? Do we use the updated or the original one? The answer is left to the reader. You can compare it in the computer simulation.
The complete algorithm is shown below:(Notice in each loop, first compute sparse component \\(X\\), then sweep from \\(k=1\\) to \\(K\\) to obtain \\(D\\) and \\(X\\), then goes to the next iteration.)

Any comments are welcome. Tks.