一种用于视觉识别的快速知识蒸馏框架

Posted 2022-12-04 AI浩

文章目录

• 摘要
• 1 简介
• 2 相关工作
• 3 方法
• • 3.1快速知识蒸馏
  • 3.2更高的标签质量
  • 3.4用监督方案训练自监督模型
  • 3.5 标签压缩与存储分析
• 4 实验
• • 4.1 监督学习
  • 4.2 ReaL[1]和ImageNetV2[27]数据集的更多比较
  • 4.3 Self-Supervised学习
  • 4.4 迁移学习
• 5 结论

摘要

论文和项目网址：http://zhiqiangshen.com/projects/FKD/FKD_camera-ready.pdf
代码：https://github.com/szq0214/FKD
虽然知识蒸馏(KD)在许多可视化任务中被认为是一种有用的工具，如监督分类和自监督表示学习，但普通KD框架的主要缺点是它的机制在通过巨大的教师网络转发时消耗了大部分计算开销，使整个学习过程效率低下和成本高昂。最近提出的解决方案ReLabel建议为整个图像创建一个标签映射。在训练过程中，它通过对齐预生成的整个标签图的RoI接收裁剪的区域级标签，这允许高效的监督生成，而不必重复通过教师。然而，由于ReLabel采用的预训练教师来自传统的多作物方案，该技术在全局标签映射和区域级标签之间存在各种不匹配，导致性能较普通 KD差。在本研究中，我们提出了一个快速知识蒸馏(FKD)框架，该框架复制了蒸馏训练阶段，并使用多作物KD方法生成软标签，同时由于没有使用RoI对齐和softmax操作等后处理，因此训练速度比ReLabel更快。当对同一幅图像进行多次裁剪以加载数据时，我们的FKD比传统的图像分类框架更有效。在ImageNet-1K上，我们在ResNet-50上获得了80.1%的Top-1精度，比ReLabel高出1.2%，同时训练速度更快，使用更灵活。在基于蒸馏的自我监督学习任务中，我们也证明了FKD具有效率优势。

1 简介

知识蒸馏(KD)[16]已被广泛应用于各种视觉领域，如监督识别[29,49,48,23,34,2]和自监督表示学习[32,9,4]。KD的机制是迫使学生模仿教师网络或集体教师的输出，并趋同于基本真理标签。已知迭代(t)时目标学生的参数θ，通过对包含两项的以下目标求最小值，可以得到下一个迭代的参数${\theta }^{(t+1)}$:
$$\begin{array}{c}{\mathbf{\theta }}_{\text{student }}^{(t+1)}=\arg {\min }_{\theta \in \Theta }\frac{1}{N}{\sum }_{n=1}^N(1-\lambda )\mathcal{H}\left({\mathbf{y}}_n,{\mathbf{S}}_{\theta }\left({\mathbf{x}}_n\right)\right)\\ +\lambda \mathcal{H}\left({\mathbf{T}}^{(t)}\left({\mathbf{x}}_n\right),{\mathbf{S}}_{\theta }\left({\mathbf{x}}_n\right)\right)\end{array}\text{\hspace{1em}(1)}$$

其中${\mathbf{y}}_n$为第n个样本的ground-truth。${\mathbf{T}}^{(T)}$是迭代(T)时老师的输出，${\mathbf{S}}_{\theta }\left({\mathbf{x}}_n\right)$是学生对输入样本的预测,${\mathbf{x}}_n.\mathcal{H}$为交叉熵损失函数。$\lambda$是平衡两个目标的系数。第一项的目标是最小化一个热点的ground-truth标签和学生预测之间的熵，第二项的目标是最小化教师和学生预测之间的熵。教师可以通过监督或自我监督的方式进行预训练。许多文献[35,52,2,34]已经经验表明，在ImageNet[7]等具有更多培训预算的大规模数据集上，如果教师或集成的教师足够准确，则不需要Eq. 1中的真硬标签第一项。在此工作中，我们简单地将快速蒸馏设计中教师和学生模型之间的软预测最小化。

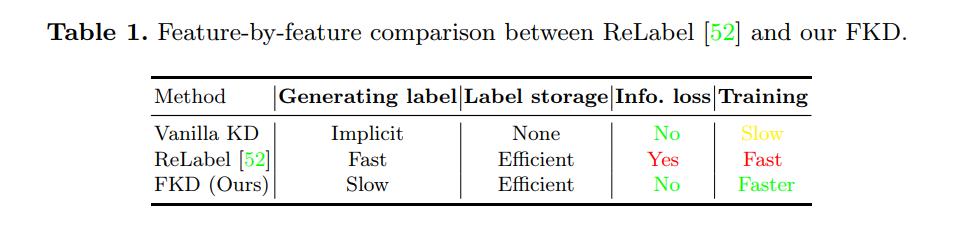
根据KD的定义，这种范式的固有缺点是，在每次迭代中，通过大型教师网络传递训练数据以产生监督${\mathbf{T}}^{(T)}$消耗了相当大比例的计算资源，而不是更新或训练目标学生参数。直观地说，通过教师的正向传播可以跨时代共享，因为他们的参数在整个培训过程中都是固定的。基于此观点，普通蒸馏框架本身效率低下，如何减少或共享跨时代教师网络的前向计算成为KD框架加速的核心。克服这一缺陷的自然解决方案是预先为每个训练图像生成一个概率向量作为软标签，然后循环重用预先生成的软标签，用于不同的训练阶段。然而，在现代神经网络训练中，通常采用各种数据增强策略来避免过拟合，特别是随机裁剪技术。这就导致了全局层面的整个图像软向量在应用这些增强后，不能精确反映局部图像区域的真实概率分布的不一致性。
为了解决数据增强的问题，在生成一个全局向量到区域级输入时，特别的随机裁剪会导致不一致的问题，同时，为了保留信息性软标签的优势，ReLabel[52]建议存储来自预训练的强教师的全局标签映射，并通过RoI对齐[13]重用epochs，如图1(左)所示。但是，由于对教师的输入过程不一致，该策略在本质上不等同于普通KD程序。不匹配主要来自两个因素:(i)教师通常使用随机裁剪调整尺寸的方案进行训练，而在重新标记中，全局标签映射是通过输入整个图像获得的。由于在蒸馏过程中，输入空间采用了随机裁剪大小调整的方法，使得全局标签映射不能反映图像区域的真实软分布;(ii) RoI对齐会涉及标签映射上的意外预测，不能保证该策略与普通KD的一致性，因此存在信息损失。

在本研究中，我们引入一种快速知识蒸馏(FKD)框架，以克服不匹配的缺点，进一步避免软标签上的信息丢失。我们的策略很简单:如图1(右)所示，在标签生成阶段，我们将多个随机裁剪的软概率直接存储到标签文件中，以及坐标和翻转等其他数据增强状态。在训练过程中，我们将这些存储的坐标分配回输入图像，生成经过网络的裁剪调整大小的输入，并使用相应的软标签计算损失。这种策略的优点有两个:(i)我们基于区域的标签生成过程与普通KD相同，因此得到的每个输入区域的软标签与oracle相同，说明在标签创建阶段没有信息丢失;(ii)我们的训练阶段速度更快，因为不需要后期处理，如RoI对齐、softmax等。我们可以进一步在一个小批处理中从同一个图像分配多个区域，以减轻数据加载的负担。

我们展示了FKD在监督和自我监督学习任务的准确性和训练速度方面的优势。在监督学习场景中，我们在各种骨干网架构(如cnn、视觉转换器和具有预训练初始化的竞争MEAL V2框架)上从零开始比较基线ReLabel和香草KD (Oracle)。我们的FKD比ImageNet-1K上的ReLabel高1%以上，速度略快，比性能相似的oracle KD和MEAL V2快3 ~ 5倍。在自监督蒸馏任务中，我们使用S2-BNN作为基线来验证我们提出的高效框架的速度优势。
我们对这项工作的贡献:

• 我们提出了一个快速知识蒸馏(FKD)框架，它实现了与香草KD相同的高水平性能，同时保持了与非KD方法相同的快速训练速度和效率，而不牺牲性能。

• 我们发现，在图像分类框架中，一个图像可以在一个小批中使用多个作物多次采样，以方便数据加载和加速训练，同时获得更好的性能。

• 为了证明我们方法的有效性和多功能性，我们在各种任务和蒸馏框架上执行FKD，包括监督分类和自我监督学习，其结果优于现有技术。

2 相关工作

知识蒸馏。 知识蒸馏[16]背后的原则是鼓励学生模仿或模仿老师的预测，这有助于学生更好地在看不见的数据上进行归纳。KD的一个核心优势是，与传统的单热标签相比，教师可以提供包含更丰富的输入数据信息的软化分布，特别是在输入空间上使用随机裁剪等数据增强时。精馏可以在每次迭代中通过强教师预测错误的标签，从而避免错误的标签，反映了转换后的输入数据的真实情况。我们还可以对logits施加温度，以重新缩放来自教师和学生模型的输出分布，以放大监督上的班级间关系。最近，许多变体和扩展被提出[24,18,44,53,23,25,34,48,50,6,36]，如采用内部特征表示[29]，带有鉴别器的对抗训练[31]，转移流[49]，对比蒸馏[40]，耐心和一致[2]等。有关知识蒸馏相关方法的更广泛概述，请参见[11,43]。

高效的知识蒸馏。 提高知识蒸馏的训练效率是将该技术在现实应用中推广到更广泛的应用范围的关键。以前在这方面的努力通常是不够的。ReLabel[52]是最近提出的一个解决方案，它可以很好地解决KD的这个低效问题。它为强教师生成全局标签映射，然后通过跨不epochs的RoI对齐重用它们。我们提出的FKD在本质上是不同的考虑和解决方案。我们考虑普通KD的特性，从强教师中随机裁剪出区域级软标签，并将其存储起来，然后在训练中通过分配到不同的时期进行重用。我们的方法具有与普通KD相同的准确性，以及与常规非KD分类框架相同或更快的训练速度，这使得它在性能和训练速度上都优于ReLabel。

3 方法

在本节中，我们首先介绍来自ReLabel的全局级软标签和FKD的区域级软标签分布的几个观察结果和属性。然后，给出了FKD框架的详细工作流程，并详细分析了生成的标签质量、训练速度以及对监督学习和自监督学习的适用性。最后，我们分析了不同的软标签压缩策略，并给出了它们在实际应用中的存储需求。
初步结论:以前解决方案的局限性

基于RoI在全局地图上对齐的ReLabel机制，与区域级软标签的普通KD相比，它是一种不可避免的标签信息丢失的近似解。在图2中，我们将ReLabel和FKD在ImageNet-1K上的区域级标签分布可视化，注意到以下几点经验观察:(i)在许多情况下，ReLabel对区域更有信心，因此软信息比FKD更弱。我们分析这是因为，ReLabel将全局图像输入到网络中，而不是局部区域，这使得生成的全局标签映射对更多的类别信息进行了编码，忽略了背景，使得软标签过于接近语义的ground-truth，如图2(第1行)所示。尽管有时ReLabel和FKD的最大概率相似，但FKD在标签分布中包含了更多的信息性的次级概率。而ReLabel等分布，如图2(第二行)所示;(ii)对于某些离群区域，FKD的鲁棒性要明显强于ReLabel，例如对象的松散边界盒、局部对象等，如图2(第3行)所示;(iii)在某些特定情况下，ReLabel意外崩溃，且分布接近均匀，而FKD仍能正常工作，如图2最下面一行所示。

此外，在KD中使用更多的数据增强(如Flip、Color jittering等)时，由于这些增强是在训练过程中随机应用的，因此ReLabel的软标签与oracle teacher prediction之间存在不匹配。在ReLabel设计中，我们在生成全局标签映射时不能考虑到这些因素，也不能提前准备。相比之下，FKD足以处理这种情况:它可以轻松地涉及额外的增强，并从相同或不同的图像中记录单个区域的所有信息(比例、度、系数等)，并通过将转换后的图像区域输入预先训练过的教师网络生成相应的软标签。然而，这种策略将增加存储的需求，因此，如果有预算，替代方案是在训练期间接收裁剪图像区域后执行额外的扩充，类似于ReLabel。注意，这将导致转换后的样本与对应的软标签之间有轻微的不匹配，这与传统的增强机制类似，但带有软标签。

3.1快速知识蒸馏

在传统的视觉训练系统中，深度网络传播和数据加载通常是资源的两大瓶颈。然而，在蒸馏框架中，除了这些计算需求外，庞大的教师一直是关键的训练负担。我们的FKD寻求解决这个棘手的问题。
标签生成阶段。 我们采用常规的随机裁剪调整训练策略，从一张图像中随机裁剪M个区域，并对其进行翻转等增宽，然后将这些区域输入到教师网络中，生成相应的软标签向量${\mathbf{P}}_i$,即${\mathbf{P}}_i=\mathbf{T}\left({\mathbf{R}}_i\right)$，其中${\mathbf{R}}_i$为经过变换变换的区域${\mathcal{F}}_i$， T为预训练的教师网络。I是区域索引。我们将所有区域坐标和增宽超参数$\mathcal{F}$与软标签集$\mathbf{P}$一起存储在接下来的训练阶段，如图1(右上)所示。下一节将详细分析如何将这些所需的值存储到硬盘驱动器上。

训练阶段。 在训练阶段，我们不像传统的图像分类策略那样随机生成作物，而是直接加载标签文件，并为这张特定的图像分配我们存储的作物坐标和数据增强，以准备转换后的区域级输入。相应的软标签将作为对这些区域进行培训的监督。对于交叉熵损失，目标是:$\mathcal{L}=-{\sum }_i{\mathbf{P}}_i\log {\mathbf{S}}_{\theta }\left({\mathbf{R}}_i\right)$，其中${\mathbf{S}}_{\theta }\left({\mathbf{R}}_i\right)$是学生对输入区域${\mathbf{R}}_i$的预测，$\theta$是我们需要学习的学生模型的参数。具体训练过程如图1所示。

3.2更高的标签质量

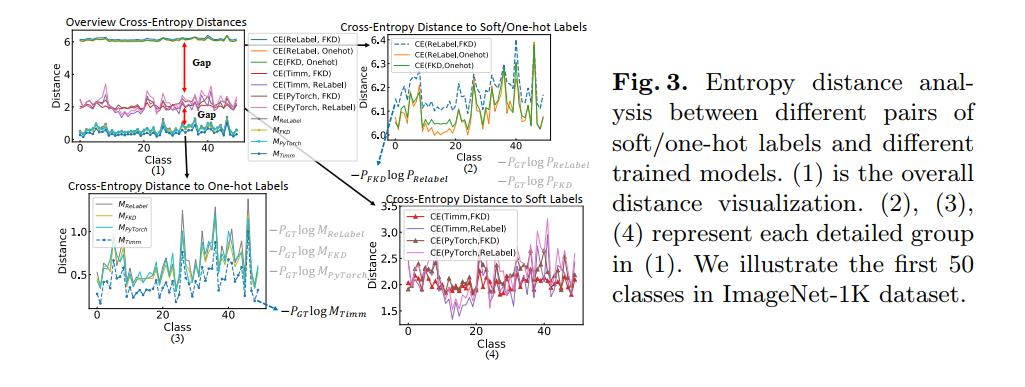
距离分析。 我们通过互交叉熵矩阵测度的熵距离来分析各种形式的标签的质量。我们考虑三种类型的标签:(1)人工注释的单热标签、ReLabel和我们的FKD。我们还计算了四种不同精度预训练模型的预测距离，包括vanilla PyTorch预训练模型(最弱)、Timm预训练模型、ReLabel预训练模型和FKD预训练模型。我们的插图的概述如图3所示。上面的曲线，以及(2)，是50个类(ReLabel!FKD)， (ReLabel!One-hot)和(FKD!One-hot)的平均交叉熵。在这里，我们得到了一个重要的观察结果:
$$\left({\mathcal{D}}_{R\to F}^{CE}=-{\mathbf{P}}_{FKD}\log {\mathbf{P}}_{\text{ReLabel }}\right)>(\begin{array}{lll}{\mathcal{D}}_{R\to O}^{CE}& \text{ OR }& {\mathcal{D}}_{F\to TPAMI2021\; |\; 视觉智能的知识蒸馏与师生学习:回顾与展望}\end{array}$$

TPAMI2021 | 视觉智能的知识蒸馏与师生学习:回顾与展望

AI是怎么测试图像识别的，与人脸识别有何不同？

解读知识蒸馏模型TinyBert

知识蒸馏之自蒸馏

用于从数据库进行人脸检测和识别的计算机视觉应用程序（+web 界面）