基于 R的 广义线性模型分析

Posted 2023-05-11

参考技术A

只是一些杂乱的笔记，没有注明出处。

简单的逻辑回归模型 logistic regression model，适用于因变量是二分变量的分析。
回归的本质是建立一个模型用来预测，而逻辑回归的独特性在于，预测的结果是只能有两种，true or false。
在R里面做逻辑回归也很简单，只需要构造好数据集，然后用glm函数(广义线性模型（generalized linear model）)建模即可,预测用predict函数。

可以用两种形式的数据来做分析：

模型输出的结果，采用summary()来查看，可以看到具体的模型信息，回归系数，系数是否显著等。(需要注意的是，Logistic为非线性模型，回归系数是通过极大似然估计方法计算所得)
summary() 展示拟合模型的详细结果
如果某个变量有多个不同的水平，你想查看一下这个变量总体是否有统计学意义，可以做一下联合检验，用anova()来查看分析偏差表。
anova() 生成一个拟合模型的方差分析表，或者比较两个或更多拟合模型的方差分析表
结果可以这么理解，随着变量从第一个到最后一个逐个加入模型，模型的课解释方差发生变化，通过看p值，是否通过显著性检验。
说明由上述这些变量组成的模型是有意义的，并且是正确的。
anova(object = model2,test = "Chisq")

可以看到这个数据集是关于申请学校是否被录取的，根据学生的GRE成绩，GPA和排名来预测该学生是否被录取。
其中GRE成绩是连续性的变量，学生可以考取任意正常分数。
而GPA也是连续性的变量，任意正常GPA均可。
最后的排名虽然也是连续性变量，但是一般前几名才有资格申请，所以这里把它当做因子，只考虑前四名！
而我们想做这个逻辑回归分析的目的也很简单，就是想根据学生的成绩排名，绩点信息，托福或者GRE成绩来预测它被录取的概率是多少！
结果解读：

根据对这个模型的summary结果可知：
GRE成绩每增加1分，被录取的 优势对数(log odds) 增加0.002
而GPA每增加1单位，被录取的优势对数(log odds)增加0.804，不过一般GPA相差都是零点几。
最后第二名的同学比第一名同学在其它同等条件下被录取的优势对数(log odds)小了0.675，看来排名非常重要啊！！！
这里必须解释一下这个优势对数(log odds)是什么意思了， 如果预测这个学生被录取的概率是p，那么优势对数(log odds)就是log2(p/(1-p)),一般是以自然对数为底。

glmer()模型下，需要用Anova 大写，Anova(model,type=3)来查看卡方值和p值，这样输出结果和jamovi是相同的。

R语言-广义线性模型

使用场景:结果变量是类别型,二值变量和多分类变量,不满足正态分布

　　　　  结果变量是计数型,并且他们的均值和方差都是相关的

解决方法:使用广义线性模型,它包含费正太因变量的分析

1.Logistics回归(因变量为类别型)

　　案例:匹配出发生婚外情的模型

　　1.查看数据集的统计信息

2 library(AER)
3 data(Affairs,package = \'AER\')
4 summary(Affairs)
5 table(Affairs$affairs)

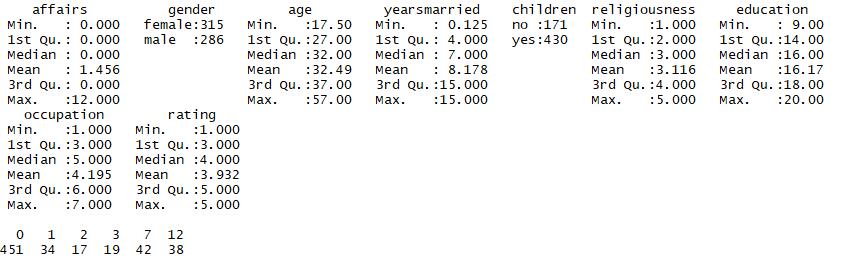
　　结果:该数据从601位参与者收集了,婚外情次数,性别,年龄,结婚年限,是否有孩子,宗教信仰,教育背景,职业,婚姻的自我评价这9个变量

　　　　 结果变量是婚外情发生的次数72%的夫妻没有婚外情,最多的是一年中每月都有婚外情占6%

　　2.将结果值转换为二值型因子

1 Affairs$ynaffair[Affairs$affairs > 0] <- 1
2 Affairs$ynaffair[Affairs$affairs == 0] <- 0
3 Affairs$ynaffair <- factor(Affairs$ynaffair, 
4                            levels=c(0,1),
5                            labels=c("No","Yes"))
6 table(Affairs$ynaffair)

　　3.将该因子作为二值型变量的结果变量

1 fit.full <- glm(ynaffair ~ gender + age + yearsmarried + children + 
2                   religiousness + education + occupation +rating,
3                 data=Affairs,family=binomial())
4 summary(fit.full)

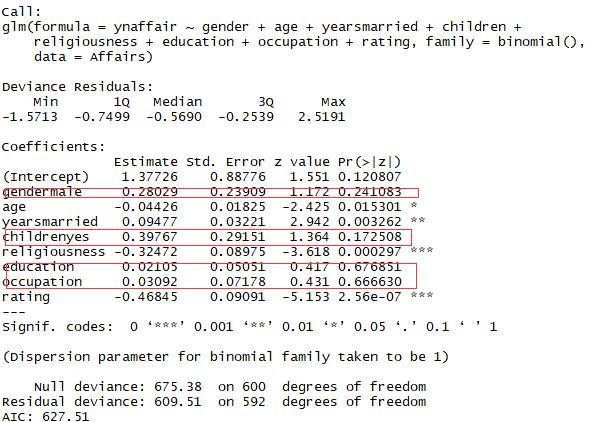
　　结果:性别,是否有孩子,学历和职业对模型不显著,去除后进行分析

1 fit.reduced <- glm(ynaffair ~ age + yearsmarried + religiousness + 
2                      rating, data=Affairs, family=binomial())
3 summary(fit.reduced)

　　3.使用卡方检验来判断比较

1 anova(fit.reduced,fit.full,test = \'Chisq\')

　　 结果:p=0.21,表示新模型的拟合更好

　　4.解释模型参数

1 coef(fit.reduced)
2 exp(coef(fit.reduced))

　　结果:婚龄每增加1岁,婚外情发生的可能性将乘以1.106,相反年龄增加1岁,婚外情发生的可能性乘以0.9652

　　5.评价婚姻评分对婚外情的影响

1 # 1.手动生成数据集
2 # 2.使用predict函数来进行预测
3 testdata <- data.frame(rating=c(1,2,3,4,5),age=mean(Affairs$age),
4                        yearsmarried=mean(Affairs$yearsmarried),
5                        religiousness=mean(Affairs$religiousness))
6 testdata
7 testdata$prob <- predict(fit.reduced,newdata = testdata,type=\'response\')
8 testdata

　　结果:当婚姻评分从1(很不幸)变成5(很幸福)的时候,婚外情发生的概率从0.53降低到0.15

　　6.评价年龄对婚外情的影响

1 testdata <- data.frame(rating=mean(Affairs$rating),
2                        age=seq(17,57,10),
3                        yearsmarried=mean(Affairs$yearsmarried),
4                        religiousness=mean(Affairs$religiousness))
5 testdata$prob <- predict(fit.reduced,newdata = testdata,type=\'response\')
6 testdata

　　结果:当其他变量不变时,年龄从17到57岁,婚外情的概率从0.34降低到0.11

　　7.判断是否过度离势

　　　　过度离势会导致标准误检验和不精确的显著性检验,此时任然可以使用gml()拟合拟合Logistics回归,但是把二项分布改为类二项分布

1 # 如果结果接近1,表示没有过度离势
2 deviance(fit.reduced)/df.residual(fit.reduced)

　　

　　结果:没有过度离势

 

2.泊松回归(因变量为计数型)

　　使用场景:通过一系列连续型或类别型预测变量来预测计数型结果变量时采用泊松分布

　　案例:药物治疗是否能减小癫痫的发病数

　　1.查看数据集

1 data(breslow.dat,package = \'robust\')
2 names(breslow.dat)
3 summary(breslow.dat[c(6,7,8,10)])

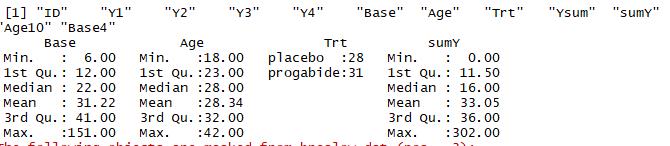
　　结果:我们分析年龄,治疗条件,前八周的发病次数和随机化后八周内的发病次数的关系,所以只采用4个变量

　　2.图形

1 opar <- par(no.readonly = T)
2 par(mfrow=c(1,2))
3 attach(breslow.dat)
4 hist(sumY,breaks = 20,xlab = \'Seizure Count\',main = \'Distribution of Sizeture\')
5 boxplot(sumY~Trt,xlab=\'Treatment\',main=\'Group Comparisons\')
6 par(opar)

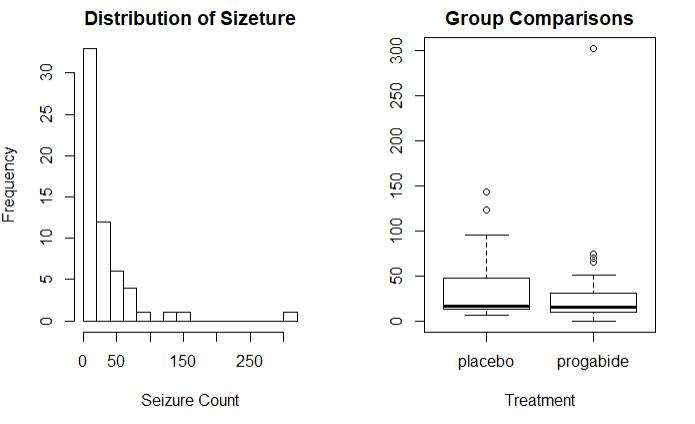
　　结果:可以看出使用药物的组,癫痫的发病率有所减少

　　3.拟合泊松回归

1 fit <- glm(sumY~Base+Age+Trt,data = breslow.dat,family = poisson())
2 summary(fit)

　　结果:偏差,回归参数,标准误差和参数为0的检验

　　4.解释模型参数

1 coef(fit)
2 exp(coef(fit))

　　结果:年龄每增加1岁,癫痫的发病数将乘以1.023,如果从安慰剂组调到药物组,则发病率会减少14%

　　5.判断是否过度离势

1 deviance(fit)/df.residual(fit)

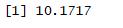
　　结果:大于1,存在过度离势

　　6.调整模型

1 fit.new <- glm(sumY~Base+Age+Trt,data = breslow.dat,family = quasipoisson())
2 summary(fit.new)

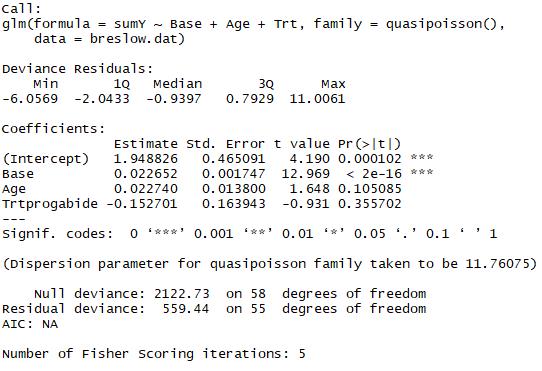
　　结果:标准误差和第一次模型相比,大了许多,同时标准误差越大会导致Trt的p值大于0.05,所以并没有充分的证据表明药物治疗相对于使用安慰剂能够降低癫痫的发病次数