leetcode 之 Merge k Sorted Lists

Posted 2022-12-03 yutianzuijin

问题来源：Merge k Sorted Lists
该问题是一个很经典的问题，给定k个有序链表将其合并成1个有序链表。很多人应该在实际的面试中遇到过该问题（至少我会经常问面试者该问题，因为接着可以问堆相关的算法~）。为啥要针对该经典问题写篇博客呢，是因为该问题确实会在日常工作中出现，但是却很少有人想到用优化的算法来解决该问题。我们先看一下该问题的两种优化解法。

解法一

最常用的方法是利用最小堆（链表升序）。将k个链表的头插入最小堆中，然后从堆中取出最小值当做新的链表头，同时将该节点的下一个节点插入堆中，重复该操作直到堆为空。假设k个链表等长，每一个长度为n，每一次堆操作复杂度都是$O(logk)$，总共有nk个元素，所以总的复杂度为$O(nklogk)$，相比naïve算法的$O(n{k}^2)$还是有比较明显的提升，特别是链表个数k特别大的时候。对应的代码如下：

struct cmp

    bool operator() (ListNode* a, ListNode* b)
    
        return a->val > b->val;
    
;
    
ListNode* mergeKLists(vector<ListNode*>& lists) 
    if(lists.size()==0) return NULL;
    ListNode* head=NULL,** cur=&head;
        
    priority_queue<ListNode*, vector<ListNode*>, cmp> q;
        
    for(auto list:lists)
    
        if(list) q.push(list);
    
        
    while(!q.empty())
    
        ListNode* t=q.top(); q.pop();
            
        *cur=t;
        cur=&(*cur)->next;
            
        if(t->next) q.push(t->next);
    
        
    return head;
 

上述代码有三点需要注意：第一，我们往堆中放的是链表节点指针，而不是节点的val值，因为只有放指针我们才能获取链表的下一个元素；第二，在生成新链表的过程中，我们利用了二级指针来简化代码，具体请参考《利用二级指针进行链表操作》，希望大家能熟练应用二级指针来操纵链表；最后，leetcode传递的参数可能会有空链表。上述代码在leetcode中的运行时间为28ms。

解法二

事实上，上面的代码还可以进一步优化。在堆操作中，我们先弹出堆顶元素，然后再push一个元素到堆中，这两个操作其实可以合二为一。当我们获取堆顶元素之后，我们不必弹出，直接将其替换成链表的下一个元素，然后再调整堆即可，这样可以避免一次堆操作，理论上速度也会更快一些。不过stl中的priority_queue不包含替换堆顶元素的函数，所以为了合二为一我们必须要自己手写堆，下面是通过手写堆进行速度优化的代码，在leetcode上的运行时间最快可以降到20ms：

void heap_fixup(vector<ListNode*> &data,int index)

    ListNode* temp=data[index];
    int parent=(index-1)>>1;
        
    while(index!=0)
    
        if(data[parent]->val<=temp->val) break;
            
        data[index]=data[parent];
                    
        index=parent;
        parent=(index-1)>>1;
    
    data[index]=temp;

    
void heap_fixdown(vector<ListNode*>& data,int index)

    ListNode* temp=data[index];
    int child=(index<<1)+1;

    while(child<data.size())
    
        if(child+1<data.size()&&data[child]->val>data[child+1]->val) child++;
            
        if(data[child]->val>=temp->val) break;
            
        data[index]=data[child];
            
        index=child;
        child=(index<<1)+1;
    
    data[index]=temp;

    
void heap_insert(vector<ListNode*>& data,ListNode* val)

    data.push_back(val);
    heap_fixup(data,data.size()-1);

    
void heap_delete(vector<ListNode*>& data)

    data[0]=data.back();
    data.pop_back();
    heap_fixdown(data,0);

    
void heap_replace_first(vector<ListNode*>& data,ListNode* val)

    data[0]=val;
    heap_fixdown(data,0);


ListNode* mergeKLists(vector<ListNode*>& lists) 
    if(lists.size()==0) return NULL;
        
    ListNode* head=NULL,** cur=&head;
    vector<ListNode*> min_heap;
        
    for(auto list:lists)
    
        if(list) heap_insert(min_heap,list);
            
        
    while(!min_heap.empty())
    
        *cur=min_heap[0];
        cur=&(*cur)->next;
            
        if(min_heap[0]->next)
            heap_replace_first(min_heap,min_heap[0]->next);
        else
            heap_delete(min_heap);
    
        
    return head;

解法三

另外一种方法利用了分支的思想，先把链表两两合并，链表个数减半；然后再两两合并，继续减半，直到只剩一个链表为止。算法复杂度为$T(k)=2T(k/2)+O(nk)$，推导得到算法复杂度为$O(nklogk)$，复杂度和解法一相同。具体代码如下：

ListNode* mergeTwoList(ListNode* a,ListNode* b)
    
    ListNode* head=NULL,**cur=&head;
        
    while(a&&b)
    
        if(a->val<b->val)
        
            *cur=a;
            a=a->next;
        
        else
        
            *cur=b;
            b=b->next;
        
        cur=&(*cur)->next;
    
        
    if(a) *cur=a;
        
    if(b) *cur=b;
        
    return head;

    
ListNode* mergeKLists(vector<ListNode*>& lists) 
    if(lists.size()==0) return NULL;
        
    int last=lists.size()-1;
    while(last!=0)
    
        int i=0,j=last;
        while(i<j)
        
            lists[i]=mergeTwoList(lists[i],lists[j]);
            i++;j--;
            if(i>=j) last=j;
        
    

    return lists[0];

在上面的代码中，我们在主函数外面实现了两个链表合并的函数，也用到了二级指针。在主函数中，外部循环通过last来标记当前所剩的链表个数，以此判断需要迭代的轮数；内部循环每次将头部和末尾的两个链表合并，并将新链表放到前面的位置，直到两个指针相遇完成一次迭代。每一层迭代，链表个数减半，所以只需要logk次即可完成迭代。上述代码在leetcode上的运行时间为24ms。

实际应用

在语音识别中采用的解码算法通常为token passing算法，简单描述就是在解码网络中维护一系列token用来保存到某节点或边的局部得分，加上该点或边的声学或者语言模型得分，然后向其相邻的所有后续节点或者边传递新的token。

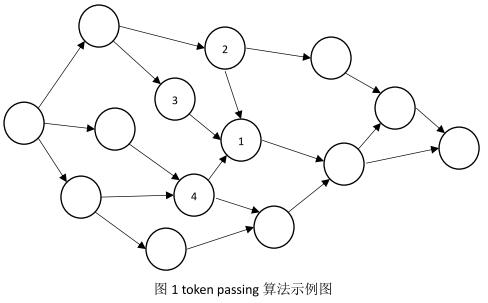
例如在图1中，节点2,3,4分别维护了到当前时刻各自节点的最优路径集合，放在其token list中。每个节点都需要往节点1传递自身的token list。节点1将节点2,3,4传递过来的token list合并成1个，然后加上自身节点的声学或者语言模型得分生成新的token list。
token passing算法本质上是一种push模式的算法，主动将token list向后续点或者边推送，push模式符合直观理解，实现简单，是目前的主流方法。与此相反的，pull模式则是点或者边主动从所有的上游点或者边获取得分，但是pull模型需要实时维护自己的上游节点有哪些，此外由当前时刻的活跃节点我们无法知道下一时刻的活跃节点有哪些，所以也无法采用pull模式。
我们可以将merge k sorted list的快速算法引入token passing算法中。具体做法是：当前位置的token list在往相邻位置传递时，我们只告诉相邻位置当前位置会往你处传递token list，而不做具体的合并。按照传统的push模式，当完成一轮遍历之后，会产生新的候选活跃节点或者活跃边，并且每个活跃节点或者活跃边的token list已经由上游节点的token list完成合并。但是在新方法下，每个活跃节点或者活跃边的token list还没有生成，生成的只是一个上游节点或者上游边的集合。有了点或者边的集合之后，我们就用快速算法对多个token list链表进行合并操作。通过上述修改我们可以使解码速度提升10%左右。