[数据结构]Graph之深度优先遍历（DFT）及广度优先遍历（BFT）

Posted 2022-12-03 yccy1230

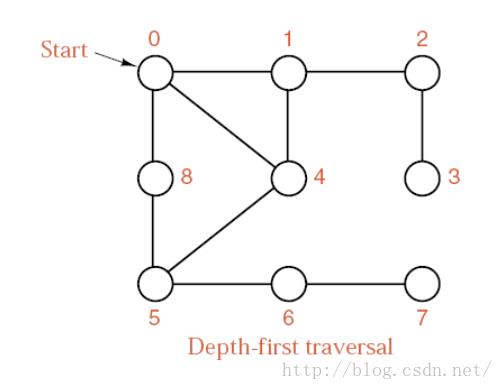
写在前面：以下图的实现采用邻接表的形式，看之前注意一下

一、广度优先遍历

遍历规则：

假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点)，则深度优先遍历可定义如下：首先访问出发点v，并将其标记为已访问过；然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止。---------百度百科

简单来说，就是对一个图进行遍历，遍历过程中对一条路径尽可能深的遍历，直至“无路可走”，再返回上一个节点判断其是否存在可走的路径

算法描述：递归实现

准备：建立一个visited[max_size]数组，用于记录顶点是否被访问过

base case：若传入顶点的每个“邻居”都已经被访问过，则结束当前递归

general case：对传入顶点进行访问，并对当前顶点的“邻居”进行判断，若存在未被访问的“邻居”，则转换为对该顶点的访问

实现代码：

template<int max_size>
void Graph<max_size>::depth_First(void(*visit)(Vertex &)) const

	bool visited[max_size];		//记录点是否已被访问
	for (int i = 0; i < max_size; i++)visited[i] = false;
	for (Vertex v = 0; v < count; v++) 
		if (!visited[v])tranverse(v, visited, visit); //对第一个节点开始递归
	

template<int max_size>
void Graph<max_size>::tranverse(Vertex & x, bool visited[], void(*visit)(Vertex &))const

	visited[x] = true;			//对当前节点进行访问
	(*visit)(x);					//并将改点置为已访问
	for (int i = 0; i < neighbours[x].size(); i++) 	
		Vertex w;
		neighbours[x].retrieve(i, w);
		if (!visited[w])tranverse(w, visited, visit);	//转换为对没有被访问过的节点的遍历
	

-------------------------------------------------------------------------------

二、广度优先遍历

遍历规则：

1、从图中某个顶点V0出发，并访问此顶点；

2、从V0出发，访问V0的各个未曾访问的邻接点W1，W2，…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点；

3、重复步骤2，直到全部顶点都被访问为止。

-------百度百科

百科的叙述已经挺清楚了，用再直白的话说，就是对一个图进行访问，首先对起点访问，然后对起点 的每一个“邻居进行访问”，都访问完了再对每个“邻居”的“邻居”进行访问。

额。。。好像讲的有点绕了，反正就好像一层一层的遍历一样，尽可能的“广”。

算法描述：

准备：建立一个visited[max_size]数组，用于记录顶点是否被访问过

    建立辅助队列

将第一个顶点做入队操作

若队列中的第一个元素未被访问，则访问，并将其所有“邻居”进行入队操作

将队首元素pop出来

对队列的现队首重复上述操作，直至队列为空

实现代码：

template<int max_size>
void Graph<max_size>::breadth_first(void(*visit)(Vertex &)) const

	queue<Vertex> q;
	bool visited[max_size];
	for (int i = 0; i < max_size; i++)visited[i] = false;
	Vertex v, w, x;
	for (v = 0; v < count; v++) 		//防止出现联通分支的情况
		if (!visited[v]) 			//向队列中添加第一个顶点
			q.push(v);
			while (!q.empty()) 
				w = q.front();
				if (!visited[w]) 	//若没有被访问过，进入循环，对其所有“邻居”进行入队操作
					visited[w] = true;	//因为我们有标记是否被访问过，所以不会重复遍历
					(*visit)(w);
					for (int i = 0; i < neighbours[w].size(); i++) 
						neighbours[w].retrieve(i, x);
						q.push(x);
					
				
				q.pop();	//所有“邻居”都被入队，且当前顶点已被访问，出队
			
		
	

下面附上我的整个project，并附上我的测试用例

（我的输入是按照邻接表的行，一行一行进行输入的）

//Graph.h
#include"Linked_List.cpp"
typedef int Vertex;
template<int max_size>
class Graph

public:
	Graph();
	void inputRow(int row, int count);
	void depth_First(void(*visit)(Vertex &))const;
	void breadth_first(void(*visit)(Vertex &))const;

private:
	void tranverse(Vertex &x, bool visited[], void(*visit)(Vertex &))const;
	List<Vertex> neighbours[max_size];
	int count;

;

//Graph.cpp
#include"Graph.h"
#include<queue>

template<int max_size>
Graph<max_size>::Graph()

	count = 0;


template<int max_size>
void Graph<max_size>::inputRow(int row, int count)

	for (int i = 0; i < count; i++) 
		Vertex tmp;
		cin >> tmp;
		neighbours[row].insert(i,tmp);
	
	this->count++;


template<int max_size>
void Graph<max_size>::depth_First(void(*visit)(Vertex &)) const

	bool visited[max_size];		//记录点是否已被访问
	for (int i = 0; i < max_size; i++)visited[i] = false;
	for (Vertex v = 0; v < count; v++) 
		if (!visited[v])tranverse(v, visited, visit); //对第一个节点开始递归
	


template<int max_size>
void Graph<max_size>::breadth_first(void(*visit)(Vertex &)) const

	queue<Vertex> q;
	bool visited[max_size];
	for (int i = 0; i < max_size; i++)visited[i] = false;
	Vertex v, w, x;
	for (v = 0; v < count; v++) 		//防止出现联通分支的情况
		if (!visited[v]) 			//向队列中添加第一个顶点
			q.push(v);
			while (!q.empty()) 
				w = q.front();
				if (!visited[w]) 	//若没有被访问过，进入循环，对其所有“邻居”进行入队操作
					visited[w] = true;	//因为我们有标记是否被访问过，所以不会重复遍历
					(*visit)(w);
					for (int i = 0; i < neighbours[w].size(); i++) 
						neighbours[w].retrieve(i, x);
						q.push(x);
					
				
				q.pop();	//所有“邻居”都被入队，且当前顶点已被访问，出队
			
		
	


template<int max_size>
void Graph<max_size>::tranverse(Vertex & x, bool visited[], void(*visit)(Vertex &))const

	visited[x] = true;			//对当前节点进行访问
	(*visit)(x);					//并将改点置为已访问
	for (int i = 0; i < neighbours[x].size(); i++) 	
		Vertex w;
		neighbours[x].retrieve(i, w);
		if (!visited[w])tranverse(w, visited, visit);	//转换为对没有被访问过的节点的遍历
	

//main.cpp
#include<iostream>
#include"Graph.cpp"
using namespace std;

void visit(Vertex &x) 
	cout << x << ' ';


int main() 
	Graph<10> graph;
	graph.inputRow(0, 3);
	graph.inputRow(1, 3);
	graph.inputRow(2, 2);
	graph.inputRow(3, 1);
	graph.inputRow(4, 3);
	graph.inputRow(5, 3);
	graph.inputRow(6, 2);
	graph.inputRow(7, 1);
	graph.inputRow(8, 2);
	
	graph.depth_First(visit);
	cout << endl;
	graph.breadth_first(visit);
	cout << endl;
	return 0;

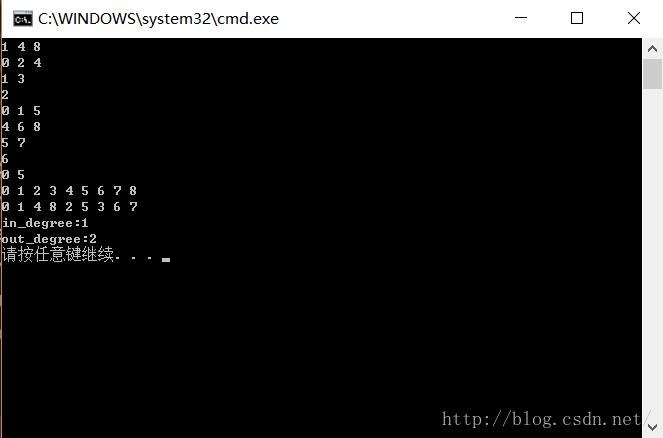
以上。

2016/6/12