算法和数据结构解析：2 - 数组问题

Posted 2022-12-03 鮀城小帅

在程序设计中，为了处理方便，常常需要把具有相同类型的若干元素按有序的形式组织起来，这种形式就是数组（Array）。

数组是程序中最常见、也是最基本的数据结构。在很多算法问题中，都少不了数组的处理和转换。

对数组进行处理需要注意以下特点：

• 首先，数组会利用 索引 来记录每个元素在数组中的位置，且在大多数编程语言中，索引是从 0 算起的。我们可以根据数组中的索引，快速访问数组中的元素。事实上，这里的索引其实就是内存地址。

• 其次，作为线性表的实现方式之一，数组中的元素在内存中是连续存储的，且每个元素占用相同大小的内存。

1. 两数之和

1.1 题目

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。(本题出自leetcode)

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9

所以返回 [0, 1]

1.2 方法一：暴力法

首先考虑暴力解法，再进行优化。暴力法，穷举所有两数组合。

暴力法其实非常简单：把所有数、两两组合在一起，计算它们的和，如果是target，就输出。

    /**
     * 方法一：暴力破解法
     * @param nums
     * @param target
     * @return
     */
    public int[] twoSum(int[] nums, int target) 

        int n = nums.length;
        for(int i=0;i< n-1 ;i++)
            for(int j= i+1;j<n; j++)
                if(nums[i]+nums[j]==target)
                    return new int []i,j;
                
            
        
        throw new IllegalArgumentException("no solution");
    
    public static void main(String[] args) 
        int[] nums = 2,7,11,15;
        int target = 9;
        int[] result = new twoSum().twoSum(nums,target);
        System.out.print(result[0] + "\\t");
        System.out.println(result[1]);
    

输出结果：

0	1

Process finished with exit code 0

复杂度分析

1. 时间复杂度：O(n^2)，对于每个元素，我们试图通过遍历数组的其余部分来寻找它所对应的目标元素，这将耗费 O(n)。
2. 空间复杂度：O(1)。

1.3 方法二：两遍哈希表

为了对运行时间复杂度进行优化，我们需要一种更有效的方法来检查数组中是否存在目标元素。如果存在，我们需要找出它的索引。这可以使用哈希表来实现。

具体实现方法，最简单就是使用两次迭代。

在第一次迭代中，我们将每个元素的值和它的索引添加到表中；然后，在第二次迭代中，我们将检查每个元素所对应的目标元素 (target-nums[i]) 是否存在于表中。

    /**
     * 方法二：两遍哈希表
     * @param nums
     * @param target
     */
    public int[] twoSum2(int[] nums, int target)

        int length = nums.length;
        // 定义一个hash表
        Map<Integer,Integer> map = new HashMap<>();

        //1.遍历数组，将数据全部保存入hash表
        for (int i = 0;i<length;i++)
            map.put(nums[i],i);
        

        //2. 再次遍历数组，寻找每个数对应的那个数是否存在
        for(int j=0;j<length;j++)
            int cur = target - nums[j];
            // 如果那个数存在，并且不是当前数自身，就直接返回结果
            if(map.containsKey(cur) && map.get(cur) != j )
                return new int[]j,map.get(cur);
            
        
        // 如果找不到，抛出异常
        throw new IllegalArgumentException("no solution");
    

复杂度分析

1. 时间复杂度：O(N)，我们把包含有 N 个元素的列表遍历两次。由于哈希表将查找时间缩短到 O(1)，所以时间复杂度为 O(N)。
2. 空间复杂度：O(N)，所需的额外空间取决于哈希表中存储的元素数量，该表中存储了 N 个元素。

1.4 方法三：一遍哈希表

在上述算法中，我们对哈希表进行了两次扫描，这其实是不必要的。在进行迭代并将元素插入到表中的同时，我们可以直接检查表中是否已经存在当前元素所对应的目标元素。如果它存在，那我们已经找到了对应解，并立即将其返回。这样，只需要扫描一次哈希表，就可以完成算法了

    /**
     * 方法三：一遍哈希表
     * @param nums
     * @param target
     */
    public int[] twoSum3(int[] nums, int target)

        int length = nums.length;
        // 定义一个hash表
        Map<Integer,Integer> map = new HashMap<>();

        // 再次遍历数组，寻找每个数对应的那个数是否存在
        for(int j=0;j<length;j++)
            int cur = target - nums[j];
            // 如果那个数存在，并且不是当前数自身，就直接返回结果
            if(map.containsKey(cur) )
                return new int[]j,map.get(cur);
            
            map.put(nums[j],j);
        
        // 如果找不到，抛出异常
        throw new IllegalArgumentException("no solution");
    

复杂度分析

1. 时间复杂度：O(N)，我们只遍历了包含有 N 个元素的列表一次。在表中进行的每次查找只花费 O(1) 的时间。其实这个过程中，我们也借鉴了动态规划的思想、把子问题解保存起来，后面用到就直接查询。
2. 空间复杂度：O(N)，所需的额外空间取决于哈希表中存储的元素数量，该表最多需要存储 N 个元素。

2.三数之和

2.1 题目（来源：力扣（LeetCode））

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例:

给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：

[

  [-1, 0, 1],

  [-1, -1, 2]

]

2.2 分析

这个问题比起两数之和来，显然要复杂了一些，而且由于结果可能有多种情况，还要考虑去重，整体难度提升了不少。

最后的返回，就不再是一个简单的数组了，而是“数组的数组”，每一组解都是一个数组，最终有多组解都要返回。

2.3 方法一：暴力法

最简单的办法，当然还是暴力法。基本思路是，每个人都先去找到另一个人，然后再一起逐个去找第三个人。

很容易想到，实现起来就是三重循环：这个时间复杂度是 O(n^3)。

    /**
     * 方法一：暴力法，三重循环遍历
     * @param nums
     * @return
     */
    public List<List<Integer>> threeSum1(int[] nums)

        int size = nums.length;
        List<List<Integer>> resultList = new ArrayList<>();
        // 三重循环，遍历所有的三数组合
        for(int i = 0; i < size-2; i++)
            for (int j = i + 1; j < size-1; j++)
                for(int k = j + 1; k < size; k++)
                    if(nums[i]+nums[j]+nums[k] == 0)
                        resultList.add(Arrays.asList(nums[i],nums[j],nums[k]));
                    
                
            
        
        return resultList;
    

    public static void main(String[] args) 
        int[]nums = -1, 0, 1, 2, -1, -4;
        threeSum threeSum = new threeSum();
        List<List<Integer>> lists = threeSum.threeSum1(nums);
        lists.stream().forEach(System.out::println);
    

运行一下，我们会发现，这个结果其实是不正确的没有去重，同样的三元组在结果中无法排除。比如-1，0，1会出现两次。而且时间复杂度非常高，是N^3。

所以接下来，我们就要做一些改进，试图降低时间复杂度，而且解决去重问题.

2. 4 方法二：暴力法改进 ： 结果去重

要做去重，自然首先想到的，就是把结果保存到一张hash表里。仿照两数之和，直接存到HashMap里查找，代码如下：

    /**
     * 方法二：暴力法改进，基于hash表去重
     * @param nums
     * @return
     */
    public List<List<Integer>> threeSum3(int[] nums)

        int size = nums.length;
        List<List<Integer>> result = new ArrayList<>();

        // 定义一个hash map
        Map<Integer,List<Integer>> map = new HashMap<>();

        // 遍历数组，寻找每个数对应的那个数
        for(int i = 0; i < size; i++)
            int thatNum = 0 - nums[i];
            if (map.containsKey(thatNum))
                // 如果已经存在thatNum，就找到了一组解
               List<Integer> tempList = new ArrayList<>(map.get(thatNum));
               tempList.add(nums[i]);
               result.add(tempList);
               continue;
            
            // 把当前数对应的两数组合都保存到map里
            for(int j = 0 ; j < i; j++)
                // 以两数之和作为key
                int newKey = nums[i] + nums[j];
                // 如果key不存在，就直接添加进去
                if (!map.containsKey(newKey))
                    List<Integer> tempList = new ArrayList<>();
                    tempList.add(nums[j]);
                    tempList.add(nums[i]);
                    map.put(newKey,tempList);
                
            
        

        return result;
    

时间复杂度降为N^2，空间复杂度O(N)。

但是，我们加一个输入[0,0,0,0]，会发现 结果不正确。

因为尽管通过HashMap存储可以去掉相同二元组的计算结果的值，但没有去掉重复的输出（三元组）。这就导致，0对应在HashMap中有一个值（0，List（0，0）），第三个0来了会输出一次，第四个0来了又会输出一次。

2.5 方法三：双指针法

暴力法搜索时间复杂度为O(N^3)，要进行优化，可通过双指针动态消去无效解来提高效率。

双指针的思路，又分为左右指针和快慢指针两种。

我们这里用的是左右指针。左右指针，其实借鉴的就是分治的思想，简单来说，就是在数组头尾各放置一个指针，先让头部的指针（左指针）右移，移不动的时候，再让尾部的指针（右指针）左移：最终两个指针相遇，那么搜索就结束了。

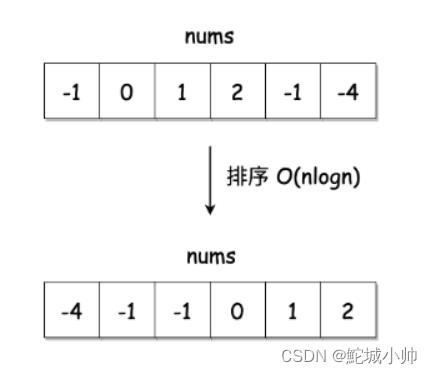
（1）双指针法铺垫： 先将给定 nums 排序，复杂度为 O(NlogN)。

首先，我们可以想到，数字求和，其实跟每个数的大小是有关系的，如果能先将数组排序，那后面肯定会容易很多。

之前我们搜索数组，时间复杂度至少都为O(N^2)，而如果用快排或者归并，排序的复杂度，是 O(NlogN)，最多也是O(N^2)。所以增加一步排序，不会导致整体时间复杂度上升。

（2）初始状态，定义左右指针L和R，并以指针i遍历数组元素。

固定 3 个指针中最左（最小）数字的指针 i，双指针 L，R 分设在数组索引 (i, len(nums)) 两端，所以初始值，i=0；L=i+1；R=nums.length-1

通过L、R双指针交替向中间移动，记录对于每个固定指针 i 的所有满足 nums[i] + nums[L] + nums[R] == 0 的 L,R 组合。

两个基本原则：

1. 当 nums[i] > 0 时直接break跳出：因为 nums[R] >= nums[L] >= nums[i] > 0，即 3 个数字都大于 0 ，在此固定指针 i 之后不可能再找到结果了。
2. 当 i > 0且nums[i] == nums[i - 1]时，即遇到重复元素时，跳过此元素nums[i]：因为已经将 nums[i - 1] 的所有组合加入到结果中，本次双指针搜索只会得到重复组合。

（3）固定i，判断sum，然后移动左右指针L和R。

L，R 分设在数组索引 (i, len(nums)) 两端，当L < R时循环计算当前三数之和：

sum = nums[i] + nums[L] + nums[R]

并按照以下规则执行双指针移动：

• 当sum < 0时，L ++并跳过所有重复的nums[L]；

1. 由于sum<0，L一直右移，直到跟R重合。如果依然没有结果，那么i++，换下一个数考虑。

 换下一个数，i++，继续移动双指针：

初始同样还是L=i+1，R=nums.length-1。同样，继续判断sum。

• 找到一组解之后，继续移动L和R，判断sum，如果小于0就右移L，如果大于0就左移R：

 

        找到一组解[-1,-1,2]，保存，并继续右移L。判断sum，如果这时sum=-1+0+2>0，（R还没变，还是5），那么就让L停下，开始左移R。

• 一直移动，又找到一组解

如果又找到sum=0的一组解，把当前的[-1,0,1]也保存到结果数组。继续右移L。

• 如果L和R相遇或者L>R，代表当前i已经排查完毕，i++；如果i指向的数跟i-1一样，那么直接继续i++，考察下一个数；

 

1. 这时i=3，类似地，当sum > 0时，R左移R -= 1，并跳过所有重复的nums[R]；

• L和R相遇，结束当前查找，i++。

 

当 nums[i] > 0 时直接break跳出：过程结束。

所以，最终的结果，就是[-1,-1,2],[-1,0,1]。

代码如下：

    /**
     * 方法三：双指针
     * @param nums
     * @return
     */
    public List<List<Integer>> threeSum4(int[] nums)

        int size = nums.length;
        List<List<Integer>> result = new ArrayList<>();

        // 先对数组进行排序
        Arrays.sort(nums);

        // 遍历每一个元素，作为当前三元组中最小的那个（最矮个做核心）
        for (int i = 0; i < size; i++)
            // 如果当前数已经大于0，直接退出循环
            if (nums[i]>0)
                break;
            
            // 如果当前数据已经出现过，直接跳过
            if (i > 0 && nums[i] == nums[i-1])
                continue;

            // 常规情况，以当前数做最小数，定义左右指针（索引位置）
            int lp = i + 1;
            int rp = size - 1;
            // 只要左右指针不重叠，就继续移动指针
            while( lp < rp )
                int sum = nums[i] + nums[lp] + nums[rp];
                // 判断sum,与0做大小对比
                if (sum == 0)
                    // 等于0，就是找到了一组解
                    result.add(Arrays.asList(nums[i],nums[lp],nums[rp]));
                    lp ++;
                    rp --;
                    // 如果移动之后的元素相同，直接跳过
                    while (lp < rp && nums[lp] == nums[lp - 1]) lp++;
                    while (lp < rp && nums[rp] == nums[rp + 1]) rp--;
                
                // 小于0，较小的数增大，左指针右移
                else if (sum < 0)
                    lp ++;
                // 大于0，较大的数减小，右指针左移
                else if (sum > 0)
                    rp --;
            
        
        return result;
    

复杂度分析：

• 时间复杂度 O(N^2)：其中固定指针k循环复杂度 O(N)，双指针 i，j 复杂度 O(N)。比暴力法的O(n^3)，显然有了很大的改善。
• 空间复杂度 O(1)：指针使用常数大小的额外空间。

尽管时间复杂度依然为O(n^2)，但是过程中避免了复杂的数据结构，空间复杂度仅为常数级O(1)，可以说，双指针法是一种很巧妙、很优雅的算法设计。

3.下一个排列

3.1 题目说明（来源:力扣（LeetCode））

整数数组的一个 排列  就是将其所有成员以序列或线性顺序排列。

    例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

    例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
    类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
    而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须 原地 修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。

1,2,3 → 1,3,2

3,2,1 → 1,2,3

1,1,5 → 1,5,1

3.2 方法一：暴力法

最简单的想法就是暴力枚举，我们找出由给定数组的元素形成的列表的每个可能的排列，并找出比给定的排列更大的排列。

但是这个方法要求我们找出所有可能的排列，这需要很长时间，实施起来也很复杂。因此，这种算法不能满足要求。 我们跳过它的实现，直接采用正确的方法。

复杂度分析

时间复杂度：O(n!)，可能的排列总计有 n! 个。

空间复杂度：O(n)，因为数组将用于存储排列。

    /**
     * 方法一：一遍扫描
     * 思路：从后向前找到升序子序列，然后确定调整后子序列的最高位，剩余部分升序排列
     * @param nums
     */
    public void nextPermutation(int[] nums)
        int n = nums.length;

        // 1.从后向前找到升序子序列，找到第一次下降的数，位置记为k
        int k = n - 2;
        while (k >= 0 && nums[k] >= nums[k+1])
            k --;

        // 找到k，就是需要调整部分的最高位

        // 2.如果 k=-1,说明所有数降序排列，改成升序排列
        if (k == -1)
            Arrays.sort(nums);
            return;
        

        // 3.一般情况，k >= 0
        // 3.1 依次遍历剩余降序排列的部分，找到要替换最高位的那个数
        int i = k + 2;
        while( i < n && nums[i] > nums[k])
            i ++;

        // 当前的i,就是后面部分第一个比nums[k]小的数，i-1就是要替换的那个数

        // 3.2 交换i-1和k位置上的数
        int temp = nums[k];
        nums[k] = nums[i-1];
        nums[i-1] = temp;

        // 3.3 k之后的剩余部分变成升序排列，直接前后调换
        int start = k + 1;
        int end = n - 1;
        while ( start < end )
            int tmp = nums[start];
            nums[start] = nums[end];
            nums[end] = tmp;
            start++;
            end--;
        
    

复杂度分析

时间复杂度：O(N)，其中 NN 为给定序列的长度。我们至多只需要扫描两次序列，以及进行一次反转操作。

空间复杂度：O(1)，只需要常数的空间存放若干变量。

3.2 方法二：一遍扫描

首先，我们观察到对于任何给定序列的降序排列，就不会有下一个更大的排列。

例如，以下数组不可能有下一个排列：

[9, 5, 4, 3, 1]

这时应该直接返回升序排列。

所以对于一般的情况，如果有一个“升序子序列”，那么就一定可以找到它的下一个排列。具体来说，需要从右边找到第一对两个连续的数字 a[i] 和 a[i-1]，它们满足 a[i]>a[i-1]。

所以一个思路是，找到最后一个的“正序”排列的子序列，把它改成下一个排列就行了。

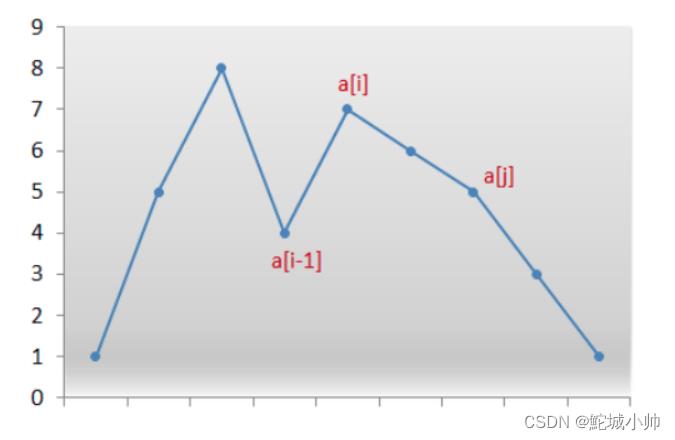
不过具体操作会发现，如果正序子序列后没数了，那么子序列的“下一个”一定就是整个序列的“下一个”，这样做没问题；但如果后面还有逆序排列的数，这样就不对了。比如

[1,3,8,7,6,2]

最后的正序子序列是[1,3,8]，但显然不能直接换成[1,8,3]就完事了；而是应该考虑把3换成后面比3大、但比8小的数，而且要选最小的那个（6）。接下来，还要让6之后的所有数，做一个升序排列，得到结果：

[1,6,2,3,7,8]

代码实现如下：

    /**
     * 方法改进：将降序数组翻转的操作提取出来
     * @param nums
     */
    public void nextPermutation2(int[] nums)
        int n = nums.length;

        // 1.从后向前找到升序子序列，找到第一次下降的数，位置记为k
        int k = n - 2;
        while (k >= 0 && nums[k] >= nums[k+1])
            k --;

        // 找到k，就是需要调整部分的最高位
        // 2.如果 k=-1,说明所有数降序排列，改成升序排列
        if (k == -1)
            reverse(nums, 0, n - 1);
            return;
        

        // 3.一般情况，k >= 0
        // 3.1 依次遍历剩余降序排列的部分，找到要替换最高位的那个数
        int i = k + 2;
        while( i < n && nums[i] > nums[k])
            i ++;

        // 当前的i,就是后面部分第一个比nums[k]小的数，i-1就是要替换的那个数
        // 3.2 交换i-1和k位置上的数
        swap(nums, k,i-1);

        // 3.3 k之后的剩余部分变成升序排列，直接前后调换
        reverse(nums, k + 1, n - 1);
    

    // 定义一个方法，交换数组中两个元素
    private void swap( int[] nums, int i, int j)
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    
    // 定义一个翻转数组的方法
    private void reverse( int[] nums, int start, int end )
        while ( start < end )
            swap(nums, start, end);
            start++;
            end--;
        
    

复杂度分析

时间复杂度：O(N)，其中 NN 为给定序列的长度。我们至多只需要扫描两次序列，以及进行一次反转操作。

空间复杂度：O(1)，只需要常数的空间存放若干变量。

4. 旋转图像（来源：力扣（LeetCode））

4.1 题目说明

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

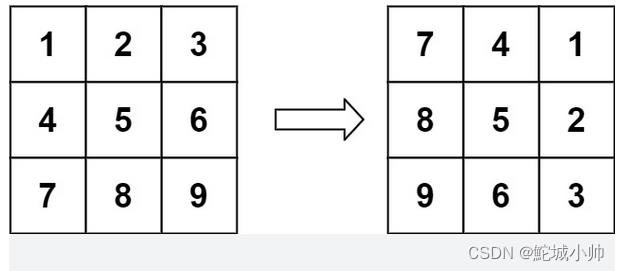
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

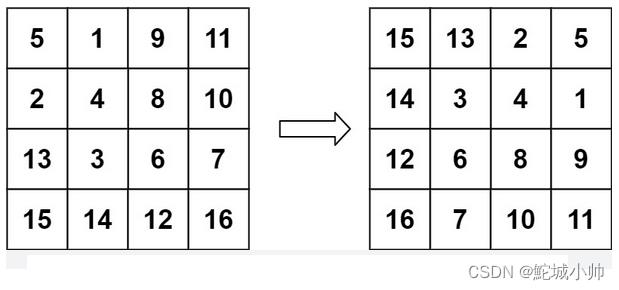
 输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

 4.2 分析

旋转图像，这个应用在图片处理的过程中，非常常见。我们知道对于计算机而言，图像，其实就是一组像素点的集合（所谓点阵），所以图像旋转的问题，本质上就是一个二维数组的旋转问题。

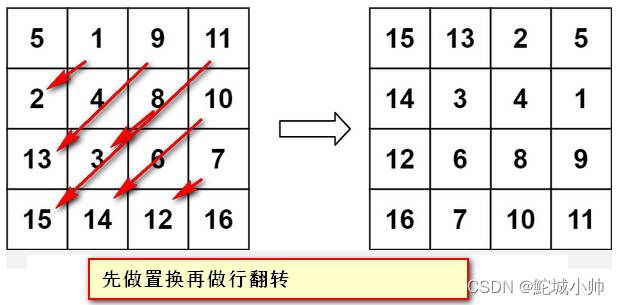
4.3 方法一：数学方法（转置再翻转）

思路：利用矩阵的特性。所谓顺时针旋转，其实就是先转置矩阵，然后翻转每一行。

public class RotateImage 

    public static void roatteImage(int[][] matrix)
        int n = matrix.length;

        // 矩阵转置，替换对角的行列值，此时i=j,行号==列号
        for ( int i = 0 ; i < n; i ++)
            for ( int j = i ; j < n; j++)
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            
        
        // 翻转每一行，取中间值，首尾互换
        for ( int i = 0 ; i < n; i ++)
            for ( int j = 0 ; j < n/2; j++)
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][n-j-1];
                matrix[i][n-j-1] = temp;
            
        
    

    public static void main(String[] args) 
        int[][] matrix = 5,1,9,11,2,4,8,10,13,3,6,7,15,14,12,16;
        roatteImage(matrix);

        for (int[] ints : matrix) 
            for (int anInt : ints) 
                System.out.print(anInt + "\\t");
            
            System.out.println();
        
    

复杂度分析

1. 时间复杂度：O(N^2)

这个简单的方法已经能达到最优的时间复杂度O(N^2) ，因为既然是旋转，那么每个点都应该遍历到，N^2的复杂度不可避免。

1. 空间复杂度：O(1)。旋转操作是原地完成的，只耗费常数空间。

4.4 方法二：

方法 1 使用了两次矩阵操作，能不能只使用一次操作的方法完成旋转呢？
为了实现这一点，我们来研究每个元素在旋转的过程中如何移动。

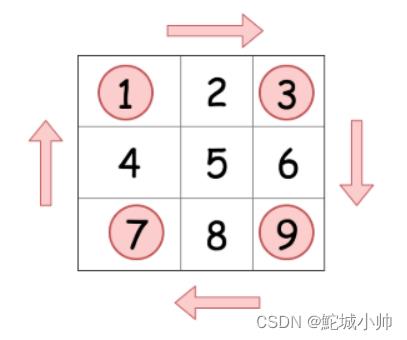
 这提供给我们了一个思路，可以将给定的矩阵分成四个矩形并且将原问题划归为旋转这些矩形的问题。这其实就是分治的思想。

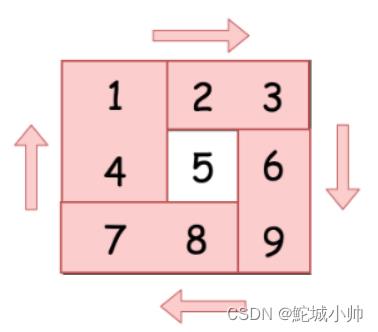
具体解法也很直接，可以在每一个矩形中遍历元素，并且在长度为 4 的临时列表中移动它们。

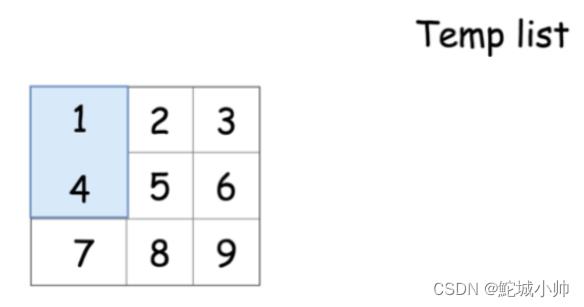
 代码如下：

    /**
     * 方法二：分治思想，分为四个子矩阵分别考虑
     * @param matrix
     */
    public static void roatteImage2(int[][] matrix)
        int n = matrix.length;

        // 矩阵转置，替换对角的行列值，此时i=j,行号==列号
        for ( int i = 0 ; i < n/2 + n%2; i ++)
            for ( int j = i ; j < n/2; j++)
                // 对于matrix[i][j]，需要找到不同的四个矩阵中对应的另外三个位置和元素
                // 定义一个临时数组，保存对应的四个元素
                int[] temp = new int[4];
                int row = i;
                int col = j;

                // 行列转换的规律：row + newCol = n - 1，col = newRow
                for ( int k = 0; k < 4; k++)
                    temp[k] = matrix[row][col];
                    int x = row;
                    row = col;
                    col = n - 1 - x;                    
                
            
        
    

复杂度分析

1. 时间复杂度：O(N^2) 是两重循环的复杂度。
2. 空间复杂度：O(1) 由于我们在一次循环中的操作是“就地”完成的，并且我们只用了长度为 4 的临时列表做辅助。

4.5 方法三：分治法改进（单次循环内完成旋转）

分成4个矩阵来旋转。这四个矩阵的对应关系，其实是一目了然的，我们完全可以在一次循环内，把所有元素都旋转到位。

因为旋转的时候，是上下、左右分别对称的，所以我们遍历元素的时候，只要遍历一半行、一半列就可以了（1/4元素）。

    /**
     * 方法三：分治法改进（单次循环内完成旋转）
     * @param matrix
     */
    public static void roatteImage3(int[][] matrix)
        int n = matrix.length;

        // 矩阵转置，替换对角的行列值，此时i=j,行号==列号
        for ( int i = 0 ; i < (n+1)/2; i ++)
            for ( int j = i ; j < n/2; j++)
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n-j-1][i];
                matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
                matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
                matrix[j][n-i-1] = temp;
            
        
    

复杂度分析

1. 时间复杂度：O(N^2)，是两重循环的复杂度。
2. 空间复杂度：O(1)。我们在一次循环中的操作是“就地”完成的。