如何利用opencv计算图像畸变系数，并进行校正与摄像机标定？

Posted 2023-05-10

如果知道图像，不知道相机还怎么通过相机来标定畸变。

1：只给定一张图片可以根据图像中相关特征进行标定，简单讲就是利用： line is straight 这个原理。

2：目前最常用的方法，是通过二维标定板，通过对 reprojection error 最小化进行非线性优化，来实现对相机的标定。并非根据看似高大上的训练集来标定。

3：畸变参数只是标定法所求参数的一部分，即：两个径向畸变系数和两个切向畸变系数。消除畸变的目的是让相机尽量地逼近针孔相机模型，这样相机成像时直线才会保持其直线性。

4：一般常见的畸变校正算法都是根据这一原理来实现的。当然，还有二般的情况。

参考技术A 如果知道图像，不知道相机还怎么通过相机来标定畸变？
1、只给定一张图片可以根据图像中相关特征进行标定，比如：图像中的某个物体具有直线性特点。一般是找出本来应当是直线的物体边缘，在其上取若干点，根据这些点将图像中的物体边缘重新校正为直线。简单讲就是利用：
line
is
straight
这个原理。
2、目前最常用的张正友在1998年提出的一种标定方法，是通过二维标定板（平面标定板），根据小孔成像的原理，通过对
reprojection
error
最小化进行非线性优化，来实现对相机的标定。并非根据看似高大上的训练集来标定。
当然他写这篇文章的目的不单单是为了校正畸变。畸变参数只是张正友相机标定法所求参数的一部分，即：两个径向畸变系数和两个切向畸变系数。
消除畸变的目的是让相机尽量地逼近针孔相机模型，这样相机成像时直线才会保持其直线性。一般常见的畸变校正算法都是根据这一原理来实现的。
当然，还有二般的情况。比如：图像中压根就没有直线性物体存在。我们该怎么办？还能进行标定吗？
答案是肯定的。可以利用对极约束，对图像畸变进行标定。不过，这需要至少两幅图像，而且这两幅图像必须是同一相机在短时间内拍摄得到。

图像校正-仿射图像的畸变校正

仿射变换

原始平面经过仿射变换后，两直线夹角会发生变化，产生畸变，如下图
仿射变换的变换矩阵为：

可以简写为：

对偶于圆点（circular point）的圆锥曲线为：

如果直线 l 和 m 在原平面上垂直，那么有：

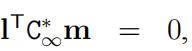
对于仿射变换的平面，可以推导出如下等式：

其中（l1’, l2’, l3’）、(m1’, m2’, m3’)分别为直线 l 和 m 的齐次坐标，令：

进而可以得到等式：

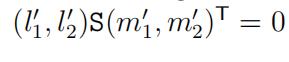
再令：

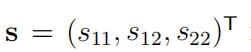
可以得到：

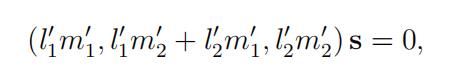
向量 s 具有两个自由度，因此只需要两个方程就能求解，进而需要找到两对在原平面互相垂直的直线。求解出向量 s 后，矩阵 S 、 K 也都能对应求解，然后代入仿射变换矩阵中，对图像平面进行逆变换，就能够消除仿射畸变。

校正步骤

仿射畸变校正是在投影畸变校正的基础上进行的，我的上一篇笔记记录了投影畸变校正的一些方法（https://blog.csdn.net/qq_44226964/article/details/121549545?spm=1001.2014.3001.5501）。
首先在图像上选取两组垂直线，其中 a ⊥ b ，c ⊥ d ，每条直线上至少找两个点以确定直线方程，如下图所示：

在求出两组垂直线的齐次坐标后，代入

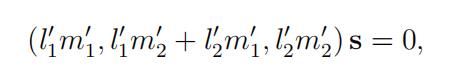
中，建立二元一次方程组（可以令S22 = 1），解出向量 s 以及矩阵 S ，矩阵 K 使用 cholesky分解 的方法求解，最后得到仿射变换矩阵 Ha，求出 Ha 的逆矩阵后，就能对原图像进行逆变换了。
最终结果如下图，从上到下依次为 原图、投影校正、仿射校正：

代码

代码中使用到的部分函数是投影校正里面的函数，在前面的文章中有，下面就没有给出来了。

void RectifyAffine()

	Mat src = imread("rectfing_projection.jpg", IMREAD_GRAYSCALE);
	IplImage* src2 = cvLoadImage("rectfing_projection.jpg");
	//使用鼠标获取点的坐标
	//GetMouse(src2);
	//手动输入上面获取的8个点，每四个点确定一组垂直线
	Point3d points_3d_8[8] =  Point3d(23, 71, 1), Point3d(101, 126, 1) ,Point3d(101, 126, 1) ,Point3d(238, 76, 1),
						 Point3d(50, 91, 1),  Point3d(196, 91, 1),  Point3d(141, 59, 1),  Point3d(101, 126, 1) ;
	//传入点和图像进行校正
	RectifyByOrthogonal( points_3d_8, src);


void RectifyByOrthogonal(Point3d points[8], Mat src)

    //通过输入的8个点得到4条连线
    vector<vector<float>> lines;
    int num_lines = 4;
    for (int i = 0; i < num_lines; i++)
    
        //获取两点连线
        GetLineFromPoints(points[2 * i], points[2 * i + 1], lines);
    
    //使用两组正交直线求解仿射变换矩阵（l1'm1', l1'm2'+l2'm1', l2'm2'）s = 0
    //先求s=（s11，s12，s22）
    vector<vector<float>> coefficients;
    for (int i = 0; i < 2; i++)
    
        vector<float> coefficient;
        coefficient.push_back(lines[i * 2][0] * lines[i * 2 + 1][0]);
        coefficient.push_back(lines[i * 2][0] * lines[i * 2 + 1][1] + lines[i * 2][1] * lines[i * 2 + 1][0]);
        coefficient.push_back(lines[i * 2][1] * lines[i * 2 + 1][1]);
        coefficients.push_back(coefficient);
    
    vector<float> s;
    ComputeEquationSet(coefficients, s);
    //计算K矩阵 S = KKT，使用Cholesky分解的方法
    vector<float> K;
    ComputeCholesky(s, K);
    //仿射变换矩阵Ha
    float Ha[3][3] =  1, 0, 0, 0, 1, 0, 0, 0, 1 ;
    Ha[0][0] = 1 / K[0];
    Ha[0][1] = 0;
    Ha[1][0] = - K[2] / K[0];
    Ha[1][1] = 1;

    Mat image = Mat::zeros(src.rows, src.cols, CV_8UC1);
    GetRectifingImage1(Ha, src, image);


void ComputeEquationSet(vector<vector<float>> coefficients, vector<float> &result)

    float a0 = coefficients[0][0];
    float b0 = coefficients[0][1];
    float c0 = coefficients[0][2];
    float a1 = coefficients[1][0];
    float b1 = coefficients[1][1];
    float c1 = coefficients[1][2];
    float s12 = (a0 * c1 - a1 * c0) / (a1 * b0 - a0 * b1);
    float s11 = -(b0 * s12 + c0) / a0;
    float s22 = 1;
    result.push_back(s11);
    result.push_back(s12);
    result.push_back(s22);


void ComputeCholesky(vector<float> s, vector<float> &K)

    float s11 = s[0];
    float s12 = s[1];
    float s22 = s[2];
    float x11 = sqrt(s11);
    float x21 = s12 / s11 * x11;
    float x22 = sqrt(1 - x21 * x21);
    //归一化
    x11 = x11 / x22;
    x21 = x21 / x22;
    x22 = 1;
    K.push_back(x11);
    K.push_back(0);
    K.push_back(x21);
    K.push_back(x22);


void GetRectifingImage1( float H[3][3], Mat& src, Mat dst)

    Size size_src = src.size();
    for (int i = 0; i < size_src.height; i++)
    
        for (int j = 0; j < size_src.width; j++)
        
            float x3 = 1;
            int x1 = Round(j * H[0][0] / x3);
            int x2 = Round((j * H[1][0] + i) / x3);
            if (x1 < size_src.width && x1 >= 0 && x2 < size_src.height && x2 >= 0)
            
                dst.at<uint8_t>(x2, x1) = src.at<uint8_t>(i, j);
            
        
    
    imshow("src1", src);
    imshow("dst", dst);
    waitKey(0);
    src = dst.clone();