A 10-bit 2.6-GS/s Time-Interleaved SAR ADC With a Digital-Mixing Timing-Skew Calibration Technique

Posted 夏风喃喃

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了A 10-bit 2.6-GS/s Time-Interleaved SAR ADC With a Digital-Mixing Timing-Skew Calibration Technique相关的知识，希望对你有一定的参考价值。

A 10-bit 2.6-GS/s Time-Interleaved SAR ADC With a Digital-Mixing Timing-Skew Calibration Technique

作者：Chin-Yu Lin, Yen-Hsin Wei, and Tai-Cheng Lee, Senior Member, IEEE
机构：Department of Electrical Engineering and Graduate Institute of Electronics Engineering, National Taiwan University, Taipei, Taiwan
期刊：IEEE JOURNAL OF SOLID-STATE CIRCUITS (JSSC)
时间：2018

摘要

一个16通道时间交错10位SAR模拟数字转换器(ADC)，采用建议的增量采样辅助SAR ADC和数字混频校准技术来补偿时序偏斜误差，实现了2.6 GS/s的采样速率。该ADC采用40-nm CMOS技术制造，在奈奎斯特速率下实现了50.6-dB的信噪失真比，而1.1-V电源的功耗为18.4 mW。在最佳情况下，数字校准可将交错杂散音从-33.6 dB提高到-63.2 dB。

关键词

增量采样辅助SAR模数转换器(ADC)、数字混频校准、品质因数(FoM)、交错杂散音、时间交错SAR ADC、时序偏斜。

文章目录

一. 介绍

最近，无线电架构，如802.11ad (WiGig)和下一代移动通信系统(5G)，要求模数转换器(ADC)的带宽超过千兆赫，有效位数为6–8位，同时保持出色的电源效率，以延长电池寿命。这意味着这类应用对ADC的多Gs/s转换速率有很高的要求。为了实现GS/s采样速率，流水线ADC因其出色的吞吐量而更受青睐。然而，需要几个高增益和宽带宽运算放大器来保持精度和线性度，从而导致功耗过大的设计。此外，先进技术中的低电源电压和降低的固有增益不利于基于运算放大器的ADC设计。另一方面，提出了时间交错来提高ADC的整体速度。此外，时间交错可以放松速度和功率的权衡，并以节能的方式降低单通道ADC的有限转换速率。此外，SAR ADC由于其简单的结构和先进技术中良好的功率效率，最近已经成为交错系统的吸引人的选择之一。SAR ADC的最佳位置位于10-bit和200–300 MS/s设计附近，适合作为一个时间交错ADC中的单元。然而，各通道之间的不匹配（如失调不匹配、增益不匹配和时序不匹配）仍会降低系统的整体性能，因此需要校准技术，交错式ADC也会有开销。失调和增益失配的校正非常简单，可以在数字域进行补偿。相比之下，时序失配更难校正，因为偏斜引起的误差取决于信号内容。探索时序偏差校准技术是本文的主要课题之一。

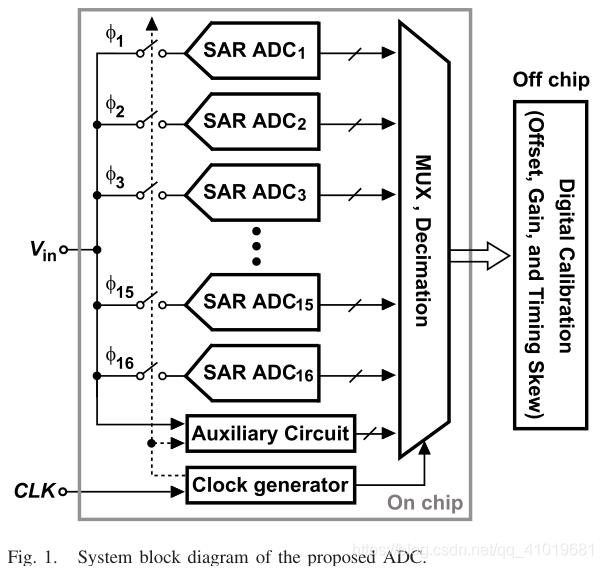
为了最大限度地减少前端采样保持（S/H）设计工作，分布式采样方案中开发了许多时间交错ADC，通过校准解决了时序偏斜问题。在模拟域或数字域中，很少有针对交错ADC的时序偏斜校准算法被报道。模拟校正的缺点包括反馈引起的稳定性危害、受控延迟线引入的抖动和长收敛时间。数字域校正利用了工艺缩放，但用于误差采集的复杂数字斜率提取滤波器限制了信号带宽。所提出的ADC展示了一种数字时序偏差校正算法结合混频信号偏斜检测的增量采样技术，实现宽信号带宽。如图1所示，10-bit 2.6-GS/s ADC通过交错16个采样速率为162.5 MS/s的SAR ADCs来实现。包括8个辅助增量采样ADC的模拟辅助电路与数字电路协作来在数字域中估计偏斜误差。之后，ADC输出经过数字校正，没有任何反馈。 除偏斜误差外，增益和失调补偿也包含在校准引擎中。校准电路的数字部分由软件实现，以证明该原型中的概念。

本文组织如下。第二节介绍了所提出的时序偏差校准的概念。第三节描述了提出的用于信号差提取的增量采样ADC架构，该架构将模拟辅助电路的开销降至最低。第四节详细介绍了原型的时间交错系统实现以及主、辅助ADC之间的失配分析。最后，第五节和第六节分别概述了实验结果和结论。

二. 建议的时序偏移校准

本节描述建议的时序校准方案。首先，将介绍用于时序偏差估计的数字混合方法。然后阐述了所提出的时序偏差校正的基本原理、结构和校准算法。最后，讨论了设计考虑和信号差异提取，这些因素减少了所建议校准的模拟设计工作。

A. 数字混频偏移检测


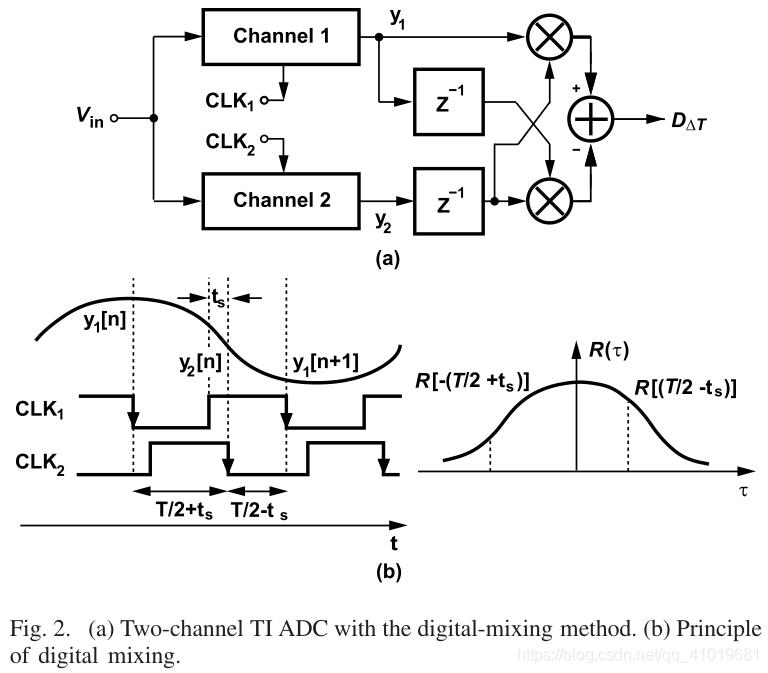
可以通过数字混频方法检测时序偏移，该方法在数字域中计算两个自相关函数值，并将它们的差作为时序偏移估计，如图2(a)所示，通过使用双通道时间交错ADC作为例子。如果没有时序偏斜，并且它们的时钟周期为 1 / f s 1/ f_s 1/fs​，则两个时钟异相。如图2(b)所示，按照通道1、通道2、然后通道1的顺序，让三个连续样本分别表示为 y [ − ( T / 2 + t s ) + n T ] y[-(T/2+t_s)+nT] y[−(T/2+ts​)+nT]， y [ 0 + n T ] y[0 + nT] y[0+nT]和 y [ ( T / 2 − t s ) + n T ] y[(T/2-t_s)+nT] y[(T/2−ts​)+nT]，其中三个自变量代表三个连续的采样时刻， T T T是每个通道的采样周期， t s t_s ts​是时序偏斜，n是离散时间索引。此外，它们相应的输出分别表示为 y 1 [ n ] y_1[n] y1​[n]、 y 2 [ n ] y_2[n] y2​[n]和 y 1 [ n + 1 ] y_1[n + 1] y1​[n+1]。通过控制双通道ADC的输出，数字混频计算两个自相关函数 R ( τ ) R(τ) R(τ)，一个来自 y [ − ( T / 2 + t s ) + n T ] y[-(T/2+t_s)+nT] y[−(T/2+ts​)+nT]至 y [ 0 + n T ] y[0 + nT] y[0+nT]的样本，另一个来自 y [ 0 + n T ] y[0 + nT] y[0+nT]至 y [ ( T / 2 − t s ) + n T ] y[(T/2-t_s)+nT] y[(T/2−ts​)+nT]的样本，如下所示：

因此，对于较小的 t s t_s ts​值，(1)和(2)之间的差值推导如下：

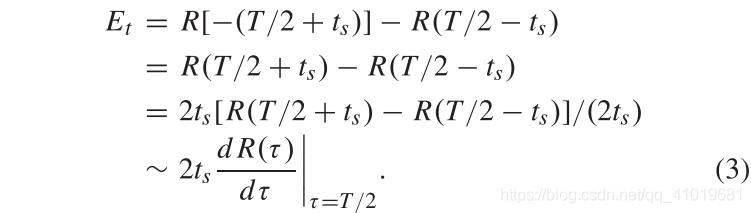
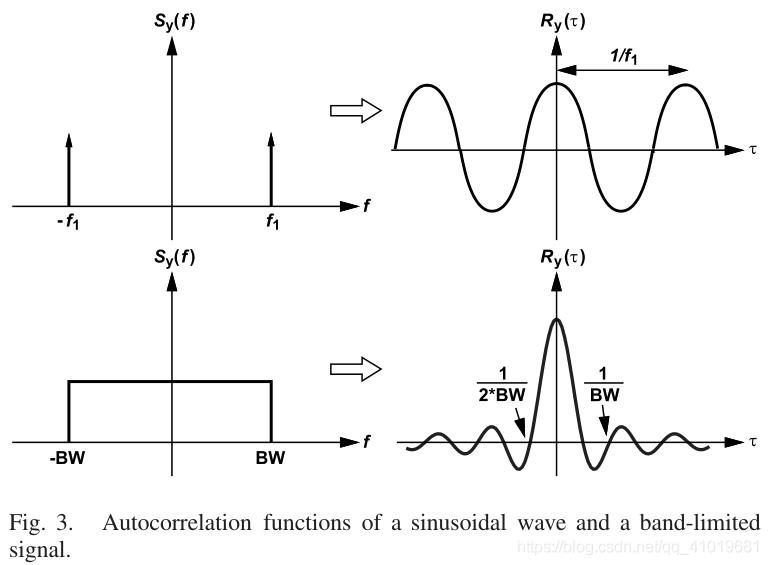
估计的时序偏差信息与偏差 t s t_s ts​成比例，比例因子取决于信号统计量，即其自相关函数的一阶导数。此外，还讨论了对不同类型信号的偏斜检测能力。图3示出了正弦波和在有限带宽上具有均匀频谱的平稳信号的自相关函数。对于频率为 f 1 f_1 f1​的正弦波，自相关是余弦波。对于带宽内频谱均匀的带限信号，自相关是 s i n c sinc sinc函数。一般来说，可以表明，对于调制和非调制信号，偏斜信息可以从它们的自相关函数围绕 τ τ τ的导数中导出。有了这些信息，通道2 ADC的采样时刻可以提前或推迟调整取决于 E t E_t Et​的极性。除了调整采样时刻，本文提出了一种数字前馈校正，带有数字混频偏斜检测，以降低模拟电路的复杂性。

B. 建议的数字时序偏移校正

在交错系统中，每个通道中的时序偏差会导致相位调制。具体来说，实际采样值和没有时序偏差的理想采样值之间的幅度差在这里称为偏差引起的采样误差。与交错式ADC中的失调和增益误差不同，采样误差本质上是输入信号频率的函数。因此，在事先不知道输入频率的情况下，操纵估计的时序偏差不能直接校正误差，因为它是输入频率的函数。相反，它需要在估计和校正之间进行一些反馈迭代，以最小化误差，直到收敛完成。文献[7]报道了全数字前馈偏斜校准。不失一般性，时序偏差被假设为比高频信号的周期小得多。然后，对于输入信号 x ( t ) x(t) x(t)，可以通过一阶泰勒级数近似对来自某个信道 i i i中的 t i t_i ti​的理想采样实例的具有时间偏斜 t s t_s ts​的采样值进行建模

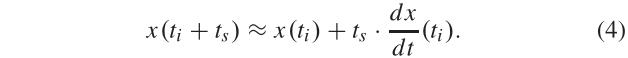
(4)右侧的第一项是理想采样值，第二项是采样误差项，由偏斜 t s t_s ts​和输入信号的一阶导数的乘积建模。或者，另一个泰勒级数近似可以表示为

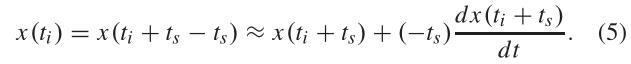
等式(5)可以视为校正等式，其中右侧的第一项是偏斜采样值，第二项是校正项。因此，我们需要知道的是信号的一阶导数，即斜率和时序偏差，才能进行采样误差校正。然而，大多数时序偏斜估计方法只确定相对时序偏斜而不是绝对值，因为它们只需要粗略估计或模拟的偏斜校准的特定时序偏斜的极性。此外，即使对于相同的时序偏差，估计量也可能不同于不同的输入统计量。因此，如果使用数字混频进行偏斜检测，则无法像[7]那样直接评估(5)。所提出的方法通过在采样点和辅助点之间进行内插或外插来估计误差，而不是计算信号导数和精确的定时偏差。如果一个辅助点 x ( t i + t s + Δ t ) x(t_i+t_s+\\Delta t) x(ti​+ts​+Δt)在采样点 x ( t i + t s ) x(t_i+ t_s) x(ti​+ts​)附近可用，(5)可以重写为

其中 K K K是常数，并且 Δ T ≪ 1 \\Delta T\\ll 1 ΔT≪1。幸运的是，如果所有估计偏斜值都与输入信号统计量成一阶比例，则该结果在分子和分母中都有估计偏斜项。随着输入统计量的变化，这些统计相关因素可以被消除，而估计的采样误差不会有缺陷。有了输入统计无关的采样误差估计在手，采样误差可以直接校正，没有任何反馈或迭代之间的估计和校正，以尽量减少误差。

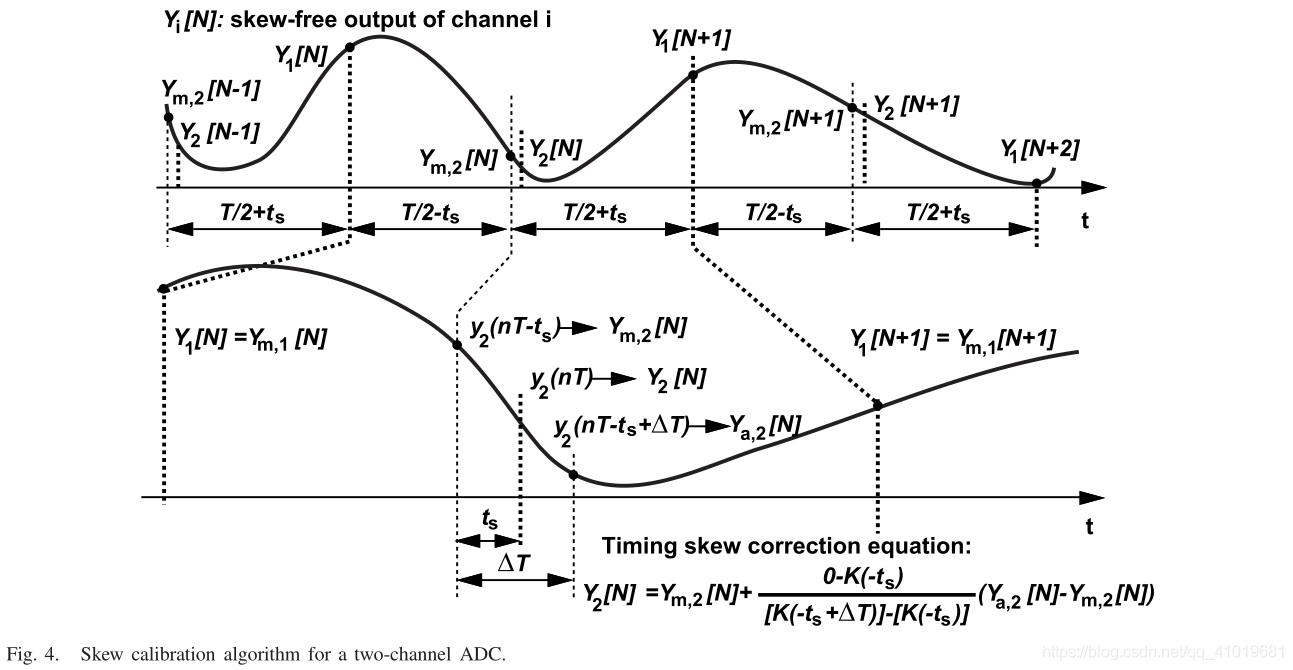
图4显示了所提出的时序偏斜校准的详细操作，为简单起见，图中显示了双通道ADC。如图4所示，无偏斜量化信道 i i i的序列表示为 Y i [ N ] Y_i[N] Yi​[N]， T T T是每个单个信道的采样周期。首先，通道1可以视为基准，由于采样电路的非理想性，通道2的采样时刻会偏斜 − t s -t_s −ts​。用于斜率估计的辅助通道2 ADC的采样时刻有意偏斜了 Δ t \\Delta t Δt来自通道2的实际采样时刻。因此，通道2用值 y ( n T − t s ) y(nT-t_s) y(nT−ts​)对输入进行采样，其相应的量化输出表示为 Y m , 2 [ N ] Y_m,2[N] Ym,2​[N]。辅助通道2用值 y ( n T − t s + Δ T ) y(nT-t_s+\\Delta T) y(nT−ts​+ΔT)对输入进行采样，量化的一个表示为 Y a , 2 [ N ] Y_a,2[N] Ya,2​[N]。如图4所示，分别是信道2和辅助信道的偏斜时间指数的 − t s -t_s −ts​和 − t s + Δ T -t_s+\\Delta T −ts​+ΔT可以通过数字混频方法来估计。对于通道2中的标称输出和辅助输出，数字混频利用ADC的输出计算通道1到通道2以及通道2到其后续通道1的自相关函数R之差。它们分别导出为(7)和(8)

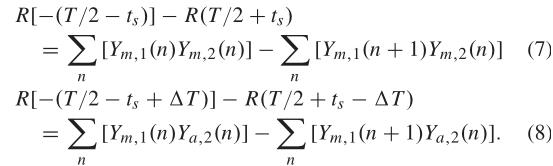
可以证明，在(7)和(8)中计算的值与主输出和辅助输出的时序偏差成比例。因此，两个输出的时序偏斜信息可以估计为两个数字量，表示为 K × ( − t s ) K×(-t_s) K×(−ts​)和 K × ( − t s + Δ T ) K×(-t_s+\\Delta T) K×(−ts​+ΔT)，其中K是一个比例因子，它依赖于信号统计量，并在第二章a节中被证明是自相关的一阶导数。

因为主信号路径和辅助信号路径对相同的输入信号进行采样时略有延迟 Δ T \\Delta T ΔT与总累计周期相比，是 T T T的倍数，因此两条路径的采样输入信号统计量可以相同。因此，假设主信号路径和辅助信号路径的 K K K保持不变是合理的。然而，采样时钟抖动可能会干扰时序偏差的测量。在这种设计中，累积16384个样本，以抑制每个校准周期的估计时序偏差。因为分别对应于主通道2、辅助通道2和理想通道2的 Y m , 2 [ N ] Y_m,2[N] Ym,2​[请教各位，10bit和12bit画面有啥区别

雪花算法python实现

C语言菜鸟问题：

10bit和12bit画面有啥区别？

10 12 14bit图像存储格式

ffmpeg+x264推送high422 10bit码流