计算机图形学学习笔记——Whitted-Style Ray Tracing（GAMES101作业5讲解）

Posted 2022-12-01 努力码代码走上人生巅峰

计算机图形学学习笔记——Whitted-Style Ray Tracing GAMES101作业5讲解

• • 遍历所有的像素生成光线
  • 光线与平面求交

遍历所有的像素生成光线

关于作业五中如何遍历所有的像素，生成光线，Ray-Tracing: Generating Camera Rays.一文中描述得非常清晰，有能力的可以直接看原文，下面我只是进行部分翻译，翻译不到位请见谅。
关于生成光线，我们需要的是找到这些像素在栅格空间（raster space）中的坐标与在世界空间(world space)中表达的相同像素的坐标之间的关系。这个过程需要几个步骤，如下图所示。

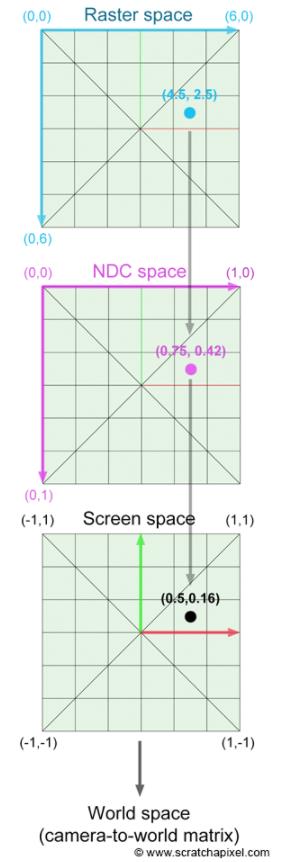
我们首先需要用每一帧的大小归一化（normalize）像素位置(pixel position)，新的归一化的像素坐标被定义在规范化设备坐标系（NDC space）：

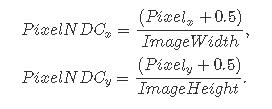
注意，我们在像素位置上增加了一个小位移(0.5)，因为我们想让最终的相机光线通过像素的中间。在NDC空间中表示的像素坐标在[0,1]范围内(是的，射线追踪中的NDC空间不同于栅格化世界中的NDC空间，后者通常映射到[-1,1]范围内)。正如在下图中所看到的（左图:一台基本相机。原始图像的大小是6x6像素，眼睛的默认位置是世界的中心(0,0,0)。注意相机是如何沿着负z轴指向的。接收平面到原点的距离正好是1个单位。右:y轴左侧和x轴下方的像素具有负世界空间坐标。），胶片或图像平面以世界坐标原点为中心。换句话说，位于图像左侧的像素应该具有负的x坐标，而位于右侧的像素应该具有正的x坐标。同样的逻辑也适用于y轴。位于x轴上的像素应该具有正的y坐标，而位于x轴下的像素应该具有负的y坐标。我们可以通过将目前在[0:1]范围内的归一化像素坐标重新映射到[-1:1]范围来纠正这个问题:

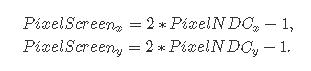
但是请注意，对于这个等式，Pixel Remappedy对于位于x轴上方的像素是负的，对于位于x轴下方的像素是正的(而它应该是相反的)。下面的公式可以解决这个问题: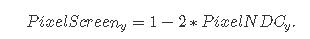
用这种方式表示的坐标称为在屏幕空间中定义。
直到现在，我们都假设图像是正方形的。计算图像宽高比非常简单。现在让我们来看一个图像尺寸为7X5像素的情况(这是一个小图像，但仍然是一个图像)。用图像的宽度除以高度得到值1.4。当像素坐标在屏幕空间中定义时，它们的范围为[- 1,1]。然而，x轴上的像素(7)比y轴上的像素(5)要多，因此，像素沿着纵轴被压缩和拉长(参见下图，左:因为图像的宽度和高度不同，像素不是平方的。为了纠正这一点，我们需要沿x轴缩放图像平面，缩放比例是图像宽高比(以像素为单位)，可以计算出图像的宽高比)。

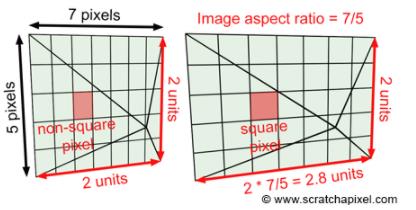
注意，这个操作保持y-像素坐标(在屏幕空间)不变。它们仍然在[-1,1]范围内，但x像素坐标现在在[-1.4,1.4]范围内(更普遍的是[-长宽比，长宽比])。

最后我们需要考虑到视野。注意，到目前为止，屏幕空间中定义的任何点的y坐标都在[- 1,1]范围内。我们还知道，成像平面距离相机原点1个单位。如果我们从侧视图看相机设置，我们可以通过连接相机的原点到胶卷平面的上边缘和下边缘来画一个三角形。因为我们知道距离相机的起源到胶片平面(一个单位)和胶片平面的高度(2单位,因为它从y = 1, y = 1),我们可以使用一些简单的三角函数来找到直角三角形ABC的角度这是一半的垂直角度α,我们感兴趣的角度是：

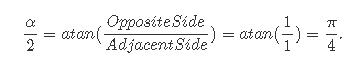
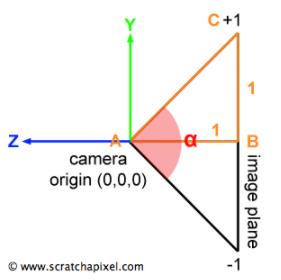
换句话说，视场角α在特定情况下是90度。现在请注意，为了计算直线BC的长度，我们需要计算角α的正切值除以2：

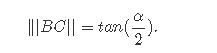
我们还可以观察到，对于大于90度的α值，||BC||大于1，对于小于90度的α值，||BC||小于1。例如α=60, tan(60/2)=0.57，如果α=110, tan(110/2)=1.43。因此，我们可以将屏幕像素坐标(目前包含在范围[- 1,1]中乘以这个数字来放大或缩小它们。正如你可能已经猜到的，这个操作改变了我们看到的场景的多少，相当于放大(当视野减小时，我们看到的场景更少)和缩小(当视野增大时，我们看到的场景更多)。总之，我们可以用角度α来定义相机的视场，并将屏幕像素坐标与这个角度的正切除以2的结果相乘(如果这个角度以角度表示，不要忘记将它转换为弧度)：

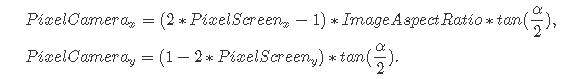
此时，原始像素坐标表示为相机的图像平面。它们已经被归一化，在[-1:1]之间映射，乘以图像长宽比，并乘以视场角αα的切线除以2。这个点位于摄像机空间中，因为它的坐标是根据摄像机的坐标系表示的。当相机处于默认位置时，相机坐标系和世界坐标系是对齐的。该点位于距离相机原点1个单位的成像平面上：

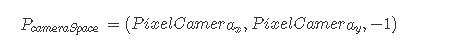
这给了我们一个像素在相机的图像平面上的位置P (PcameraSpace)。从那里,我们可以计算该像素的光线通过定义射线照相机的起源(可以称之为点O)和光线作为法线向量OP的方向(如下图)。向量OP仅仅是图像平面上的点的位置减去相机原点。当相机处于默认位置时，相机原点和世界笛卡尔坐标系是相同的，因此点O简单地为(0,0,0)。

在伪代码中，我们得到:

float imageAspectRatio = imageWidth / (float)imageHeight; // assuming width > height 
float Px = (2 * ((x + 0.5) / imageWidth) - 1) * tan(fov / 2 * M_PI / 180) * imageAspectRatio; 
float Py = (1 - 2 * ((y + 0.5) / imageHeight) * tan(fov / 2 * M_PI / 180); 
Vec3f rayOrigin(0); 
Vec3f rayDirection = Vec3f(Px, Py, -1) - rayOrigin; // note that this just equal to Vec3f(Px, Py, -1); 
rayDirection = normalize(rayDirection); // it's a direction so don't forget to normalize 

最后，我们希望能够从任何特定的角度渲染场景的图像。在将相机从其原始位置(以世界坐标系原点为中心并沿负z轴对齐)移动后，您可以用4x4矩阵表示相机的平移和旋转值。通常这个矩阵被称为相机对世界矩阵(它的逆矩阵被称为世界对相机矩阵)。如果我们这个camera-to-world矩阵应用于点O和P那么向量| | O 'P| | (其中O’是点O, P’是通过相机到世界矩阵变换的点P)表示世界空间中光线的归一化方向(如上图所示)。对O和P应用相机到世界的变换将这两点从相机空间变换到世界空间。另一个选择是在相机处于默认位置(向量OP)时计算光线方向，并将相机到世界矩阵应用到这个向量。
注意相机坐标系统是如何随着相机移动的。我们的伪代码可以很容易地修改，以考虑相机的变换(旋转和平移，缩放相机不是特别推荐):

float imageAspectRatio = imageWidth / imageHeight; // assuming width > height 
float Px = (2 * ((x + 0.5) / imageWidth) - 1) * tan(fov / 2 * M_PI / 180) * imageAspectRatio; 
float Py = (1 - 2 * ((y + 0.5) / imageHeight) * tan(fov / 2 * M_PI / 180); 
Vec3f rayOrigin = Point3(0, 0, 0); 
Matrix44f cameraToWorld; 
cameraToWorld.set(...); // set matrix 
Vec3f rayOriginWorld, rayPWorld; 
cameraToWorld.multVectMatrix(rayOrigin, rayOriginWorld); 
cameraToWorld.multVectMatrix(Vec3f(Px, Py, -1), rayPWorld); 
Vec3f rayDirection = rayPWorld - rayOriginWorld; 
rayDirection.normalize(); // it's a direction so don't forget to normalize 

为了计算最终的图像，我们需要使用我们刚才描述的方法为帧的每个像素创建一条射线，并测试这些射线中的任何一条是否与场景中的几何图形相交。

最后的代码实现与作业完全一致：

void render( 
    const Options &options, 
    const std::vector> &objects, 
    const std::vector> &lights) 
 
    Matrix44f cameraToWorld; 
    Vec3f *framebuffer = new Vec3f[options.width * options.height]; 
    Vec3f *pix = framebuffer; 
    float scale = tan(deg2rad(options.fov * 0.5)); 
    float imageAspectRatio = options.width / (float)options.height; 
    Vec3f orig; 
    cameraToWorld.multVecMatrix(Vec3f(0), orig); 
    for (uint32_t j = 0; j < options.height; ++j)  
        for (uint32_t i = 0; i < options.width; ++i)  
            float x = (2 * (i + 0.5) / (float)options.width - 1) * imageAspectRatio * scale; 
            float y = (1 - 2 * (j + 0.5) / (float)options.height) * scale; 
            Vec3f dir; 
            cameraToWorld.multDirMatrix(Vec3f(x, y, -1), dir); 
            dir.normalize(); 
            *(pix++) = castRay(orig, dir, objects, lights, options, 0); 
         
     
 
    // Save result to a PPM image (keep these flags if you compile under Windows)
    std::ofstream ofs("./out.ppm", std::ios::out | std::ios::binary); 
    ofs << "P6\\n" << options.width << " " << options.height << "\\n255\\n"; 
    for (uint32_t i = 0; i < options.height * options.width; ++i)  
        char r = (char)(255 * clamp(0, 1, framebuffer[i].x)); 
        char g = (char)(255 * clamp(0, 1, framebuffer[i].y)); 
        char b = (char)(255 * clamp(0, 1, framebuffer[i].z)); 
        ofs << r << g << b; 
     
 
    ofs.close(); 
 
    delete [] framebuffer; 
 

光线与平面求交

关于光线与平面求交，闫令琪老师的的GAMES101-现代计算机图形学入门中有详细讲解，代码这样写，更加直观：

bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2, const Vector3f& orig,
                          const Vector3f& dir, float& tnear, float& u, float& v)

    // TODO: Implement this function that tests whether the triangle
    // that's specified bt v0, v1 and v2 intersects with the ray (whose
    // origin is *orig* and direction is *dir*)
    // Also don't forget to update tnear, u and v.
    auto O = orig, D = dir, P0 = v0, P1 = v1, P2 = v2;
    auto E1 = P1 - P0, E2 = P2 - P0, S = O - P0;
    auto S1 = crossProduct(D, E2), S2 = crossProduct(S, E1);
    tnear = dotProduct(S2, E2) / dotProduct(S1, E1);
    u = dotProduct(S1, S) / dotProduct(S1, E1);
    v = dotProduct(S2, D) / dotProduct(S1, E1);
    double eps = -1e-6;
    if(tnear > eps && u > eps && v > eps && 1-u-v > eps) 
        return true;
    return false;