通俗地解释下密码学中的归约证明

Posted 2022-11-30 链巨人

本文首发于本人的：能否通俗地解释下密码学中的归约证明？ - ChainingBlocks的回答 - 知乎
https://www.zhihu.com/question/49441102/answer/1737942968

1 从问题出发

假设现在我们提出了一个密码学方案或者协议 [公式] ,我们需要证明它是安全的。怎么证明？

我们的协议一般是建立在已经被证明安全的协议/方案上面，或者建立在某些困难问题（记为Y）上面，比如RSA公钥加密算法就是建立在因数分解困难问题上。为了简化证明，站在巨人的肩膀上，我们希望通过搭建下面的逻辑命题关系来完成我们的证明。

条件命题1：只要Y是安全的，那么我们的方案 [公式] 就是安全的。换句话说，若Y被有效攻破，那么 [公式]就不再安全。

这样做的好处是，我们站在了巨人的肩膀上：我们不需要从头开始证明，而是从Y开始。大大简化我们的证明过程。

密码学中的归约证明（reduction proof）是密码学非常重要的知识。现代密码学中的几大公钥加密算法建立在几个困难问题假设上面，比如大整数因数分解困难问题（Integer factorization）和离散对数问题（Discrete log problem）。很多现代密码协议或者密码加密方案建立在这些困难问题上面，比如RSA公钥加密算法就是建立在因数分解困难问题上，因此，如果某一天该困难问题能被快速计算出来（多项式时间复杂度），那么所有建立在这个假设上面的协议/方案都变得不安全了。
根据离散数学的条件命题的逻辑等价式，若两个命题有如下关系： [公式] ，等价于 [公式] 。比如“只要晴天，我就去跑步”，等价于“如果我不去跑步，那么不是晴天”。这个命题等价式是“反证法”的基础。它被用在规约证明中证明某一个新提出的方案X的安全性（也即是下面的Thm），证明的形式为：

Thm（定理）：Y 是安全的 [公式] X是安全的。

证明：

通过等价变换，也即是要证明（记为条件命题2）：X不是安全的 [公式] Y不是安全的。

条件命题2进一步解释为：如果存在PPT的对手A可以攻破X，那么我们能构造一个PPT的敌手B来攻破Y。

其中，X是我们新提出的方案，Y某一个困难问题，PPT是多项式概率时间的英文缩写。“构造”一词可以理解为模拟。

如果我们能够让上面粗体的条件命题2成立，那么我们就完成了规约证明。这其实是一个反证法：若上面粗体的条件命题2成立，也意味着Thm成立，完成证明。

小结：现在我们明白了我们为什么要使用规约证明，以及使用规约证明的基本形式。接下来的问题是，如何来构造这个条件命题？

2 构造条件命题

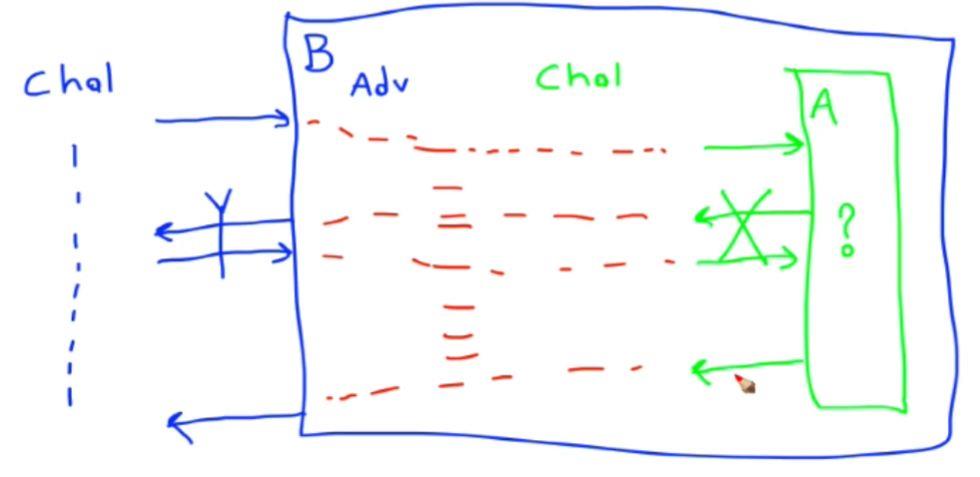
我们将上面（B,Y）和(A,X)的关系表示成下图。其中A是试图攻破X的敌手；B是试图攻破Y的敌手。A作为B的一部分，B并不知道A是如何工作的。B是A的外部环境，它要模拟对A的输入和接收A的输出，让A完成对X的攻击游戏。密码学中经常使用Game的形式来定义一个协议的安全性。虽然A的外部环境是由B模拟的，但是，我们要求该模拟的环境等价于真实的A攻击X的game的环境（或者说A无法区分其外部环境是模拟的还是真实的）。因此，这里我们也叫B为模拟器。

除了B要完成上面的工作，它还需要应对别人（B的外部环境）对它的挑战：挑战B能否攻破Y。

结合下图，intuitively，在B接收到外部环境的挑战（chel）之后，将chel进行适当变换（图中红色部分，也即是进行模拟），将其输入给A，让A挑战X。B根据A的输出，适当地变换输出值，输出给外部环境，完成挑战。因此，B对Y的挑战转嫁到A对X的挑战上了。如果我们能够将下面条件关系关联起来，就完成了证明：A对X挑战成功[公式] B对Y挑战成功，或者说 只要X不安全 -> 那么Y就不安全。

如何建模“挑战成功”？我们使用概率。在二选一的Game中，如果A成功的概率为1/2+non-neg(n),那么A就是成功的。neg（n）表示很小的值；而non-neg表示不是很小的值。同理，如果B要赢这个挑战Y的Game，其成功的概率也需要1/2+non-neg(n)。

小结：

证明过程需要：

（1）PPT：A是PPT的；红色部分的计算复杂度是PPT的。具体“红色部分”是什么呢？不同的协议不一样，下面会给出example。

（2）模拟：B所模拟A的外部环境需要看起来像“挑战X的game”的外部环境。

（3） 概率：通过概率计算出下面命题成立，来证明“A对X挑战成功 [公式] B对Y挑战成功”：P(A) = 1/2+non-neg(n) [公式] P(B) =1/2+non-neg(n)（它的逆反命题是：只要Y是安全 -> 那么X就是安全）

3 一个通俗的例子

3.1 scenario：

下面我们通过一个伪随机生成器（PRG）来构造一个单次定长的加密算法。具体为下图所示。本文默认读者知道这个知识点。需要注意的是，伪随机生成器的结果是确定的，也即是在下图s不变时，两次调用PRG得到的结果是一样的。其中s是伪随机数。

该PRG-base Enc加密方案（记为X）的intuition是，如果PRG的生成结果G(k)是随机的，那么通过与消息m异或，得到随机的密文c。

这里我们要证明命题条件：

Thm： G是安全的PRG [公式] X在Eavesdropping攻击下安全。

3.2 具体证明过程

因为B的外部环境跟A的外部环境是不一样的，所以需要B通过上图中红色的代码将B所接收到的输入进行适当转换完成模拟，再输入给A（转嫁挑战）。

红色部分的代码解释为：B接收A传来的两个消息，m0和m1，随机地选择消息m0或者m1来与r异或得到密文c。将c输入给A（转嫁挑战），A完成对X的挑战输出b’,然后B根据b和b’的关系决定B它自己对Y的挑战的结果R或者PR。R表示完全随机的，PR表示伪随机的。具体地，如果b’=b,说明A此次挑战成功，说明方案X安全性不够高，也即不是完全随机的（伪随机PR的），因此B输出PR;反之，若b’!= b，说明A此次挑战失败，说明X安全性高，完全随机的，因此B输出R。

表示X是不安全的，A挑战成功的概率为：

Pr[b’ = b] = 1/2 + non-neg(n) （1）

表示Y是不安全的，概率表示为：

Pr[B 输出 R | r is R] = Pr[B 输出R | r is PR] [公式] non-neg(n) （2）

为了将（1）和（2）联系起来，构造我们前面“只要…就…”的条件命题，于是做如下变换，我们将式（2）中的“B输出R”换成"b’[公式]b",并根据式（1）计算出式（2）变换后的概率：

等式（2）左边部分等价于 Pr[b’[公式]b | r is R] = 1/2 (请结合上面图片红色部分代码看). （3）

等式（2）右边部分等价于Pr[b’[公式]b | r is PR] = 1/2 - non-neg(n)，也即是A此次挑战失败，即用1减去式（1）得到。（4）

式（3）减（4）得到Pr[b’[公式]b | r is R] - Pr[b’[公式]b | r is Pr] = non-neg(n) （记为式（5）），它是non-negligible的，表示Y是不安全的。至此，我们推出了：只要X是不安全的（式（1）） [公式] 那么Y是不安全的（式（5））。这样我们就完成了Thm的逆反条件命题。根据条件命题等价关系，Thm得证。

------------------------内容添加-------------------------

其实不使用反证法也是可以证明X是安全的。具体为：

当输入的r是完全随机的，那么B挑战Y成功的概率是：

Pr[B® = 1] = 1/2; （6）

当输入的r是使用PRG产生的，即r=G(s), 那么B和A分别挑战Y和X成功的概率相等，因为A作为B的一部分所看到的视角，与A不作为B的一部分，在游戏中所看到的视角是一样的。即

| Pr[B(G(s)) =1] = Pr[A© = 1] | （7）(注意这里A接收输入是密文c)

因为G是伪随机生成器，并且B是PPT的，所有B无法区分完全随机的r和G(s)，所有下面两个概率只差的绝对值不大于neg(n):

| Pr [B® = 1] - Pr [B(G(s)) = 1] | <= neg(n). (8)

将式（6）和式（7）代入式（8），得到：

|1/2 - Pr[A© = 1]| <= neg(n). (9)

这推出Pr[A© =1] <= 1/2 + neg(n). 又因为A是PPT的，所以在eavesdropper下，A无法区分协议X是随机的还是伪随机的，得证。

这个证明方式参考书Introduction to Modern Cryptography, second edition, Page 69.

小结：反证法不是必须的。

reference

(梯子自备) https://www.youtube.com/watch?v=zHMecblCmAM&list=PL4wmOqlgHT2lBQfChNbkNaTlJOXrqIlHe&index=3
2. 《Introduction to Modern Cryptography, second edition》, page 65.