基于 IMU 的位姿解算

Posted 2022-11-30 一颗小树x

前言

IMU，即惯性测量元件，以牛顿经典力学定律为基本工作原理，三轴加速度计和三轴陀螺仪作为敏感元件，上电时分别输出加速度和角速度。

一般情况下，将捷联固定IMU的运动对象称为载体。当载体位姿发生变化时，可以通过初始位姿完成 IMU 采样数据在导航坐标系之间的转换，实现对载体位姿、速度等信息的计算和反馈。

解算 IMU 采样数据的过程与惯导解算技术原理有关，而提高定位精度的方法主要依赖于IMU自身精度的提高和算法改进。参考了一些论文，总结了一些IMU 位姿解算的方法和案例，记录与分享给大家。

一、IMU特点

民用的IMU，具有体积小、成本低、稳定性强等优点。但是，通常纯IMU长时间工作会导致输出数据的内部出现偏移，解算过程产出的累积误差使结果出现失真。

基于纯IMU会产生偏移的特点，通常会融合其他其他传感器；比如：在定位方面，IMU和GPS融合；IMU和磁力计融合等等。

IMMU，引入三轴磁力计的 IMU 称为惯性-磁测量元件（Inertial and Magnetic Measurement Unit，IMMU）。姿态测量方面，使用磁力数据和加速度数据来计算物 体运动时的姿态角度，对使用角速度计算所得姿态进行实时的滤波，从而提高姿态数据的精度。

二、IMU应用

1、动作捕捉：IMU动作捕捉是一种新的动捕方案，其根据是刚体铰链模型以及关节测姿。

2、状态判别：使用 IMU 进行状态判别，需要使用特定状态下的 IMU 输出进行训练，涉及智能 学习方法。

3、空间轨迹重建：IMU 在空间轨迹重建的应用以大范围导航定位为主。

4、定位：一般将 IMU 与其他传感器进行组合，即应用组合导航法。常用的组合有 IMU/UWB、IMU/视觉相机、IMU/GPS，其他可以组合的传感器包 括雷达、里程计等等。

三、IMU固定在某物体上（位姿解算）

IMU能输出了载体的加速度、角速度，通过惯导解算原理获得载体运动的位姿轨迹。进行解算时，还需要消除 IMU 采样数据中存在的误差，以 及过程中产生的误差。

将IMU 固定一个物体上，比如固定在机器人上（机器人上有个喷枪）、固定在一个装有摄像头的支架上等等，按照捷联惯导解算的原理，IMU 与固定物体的相对位置并不会发生变化，可以将 IMU的运动视作刚体运动。而刚体运动是通过位姿对时间的变化进行描述的。

3.1 坐标系转换

首先通过机器人运动学参数，将机器人的关节坐标转化为 IMU 捷联载体（喷枪）的初始位姿。

IMU 输出的是基于自身坐标系的三轴加速度和三轴角速度数据，需要转换为机器人世界坐标系下的参数信息。此处的坐标系转换参数使用姿态矩阵表示，视作姿态信息，在姿态更新环节使用初始姿态推算得出。

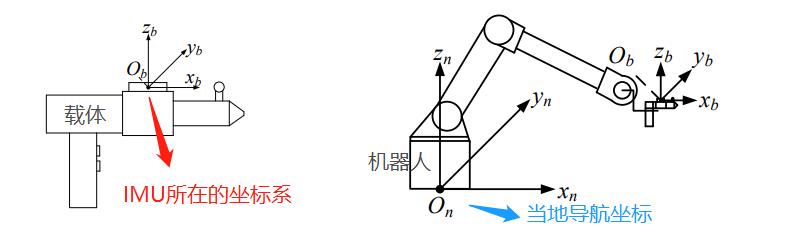
其中当地导航坐标，是惯导解算原理中的标准坐标系，解算过程需要把 IMU 输出的加速度转换到 当地导航坐标系内求解分析。

3.2 姿态更新

将 IMU 输出的加速度转换为机器人世界坐标系下 的加速度之后，根据初速对其进行二次积分，然后结合初始位置才能得到喷枪的位置信息。惯导解算原理图，包含了坐标系转换和姿态更新两个基本环节之间的关系。

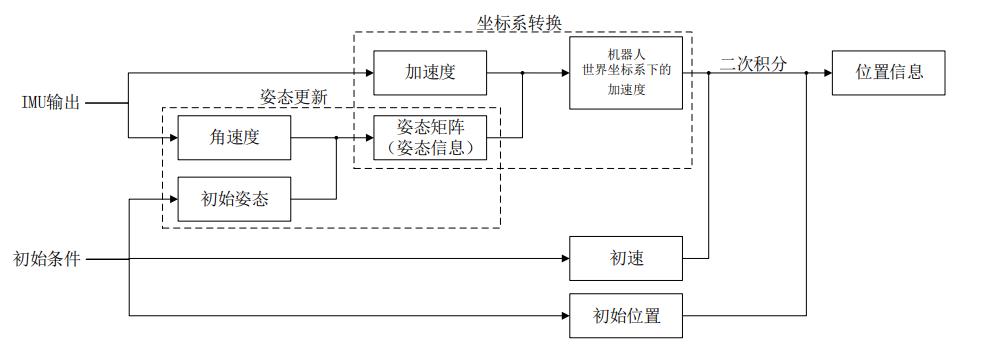
3.3 位姿解算 注意点

1、一般情况下，惯导解算需要考虑地球自转；如果研究对象的移动范围较地图定位的范围更小，因此地球转速、地球自转坐标系等因素可以忽略。

2、重力加速度一般值 g=9.8 m/s2，但建议考虑具体的地理位置进行取值，比如：研究地点在广东省珠三角地区（北纬 23°2′17.68″），重力加速度的 计算结果在 9.788 m/s2 左右浮动。

持续更新中...........

四、姿态表示法

不同坐标系之间存在着 3 自由度的位置关系和 3 自由度的姿态关系；其中3 自由度的位置关系，通常可以分别对x,y,z轴进行平移，让两个三维坐标系的原点重合。

而姿态关系，可以用欧拉角、旋转矩阵和单位四元数来表示，这三种方法在满 足一定条件时可以互相转化。

4.1 欧拉角

欧拉角是定位系统中对姿态的一种直观描述，计算时无需正交化处理，一般指航空领域主要应用的航空次序欧拉角。

假设：有两个坐标系，坐标系1记为n，坐标系2记为b。

坐标系2相对于 坐标系1的任意姿态，均能够以 坐标系1为初始状态， 绕坐标系1或自身的任意轴依次旋转 3 次获得，3 次旋转的角度统称欧拉角。

选择 z-y-x（旋转顺序）作为欧拉角的表示形 式，如下图所示：

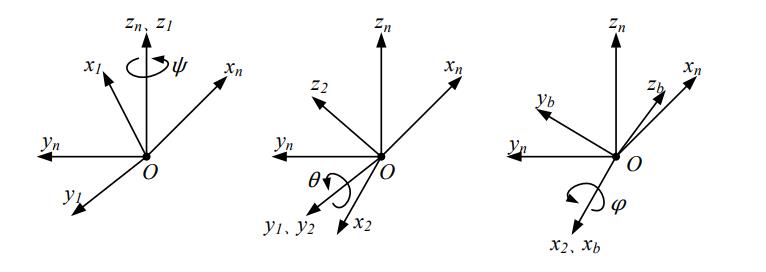
1.  先绕z轴旋转，对应偏航运动，为偏航角（yaw）
2. 然后绕y轴旋转，对应俯 仰运动，为俯仰角（pitch）
3. 最后绕x轴旋转，对应横 滚运动，为横滚角（roll）

注意：

在使用欧拉角描述物体姿态时，存在万向节死锁的问题，这导致欧拉角并不能实 现全姿态表达。例如，当俯仰角为±90°时，横滚角和偏航角将无法求出。

4.2 旋转矩阵

待完善

4.3 单位四元数

四元数符号为𝒒 ∈ 𝑅 4×1，有两种表示形式：

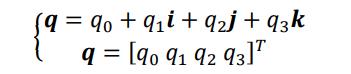
 其中，𝑞0为实数，𝑞1𝒊、𝑞2𝒋和𝑞3𝒌为虚数，此处的𝒊、𝒋和𝒌为 3 个虚单位。𝒒与𝑪𝑛 𝑏的 关系如下：

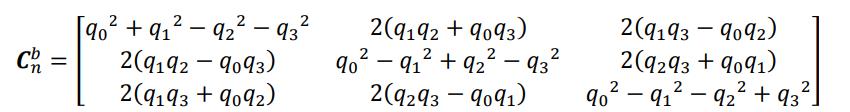
若𝒒的范数为 1，则称𝒒为单位四元数，可以表示一次旋转，用两个单位四元数相 乘表示两次旋转。

四元数𝒒用 4 个标量描述了姿态，不会存在欧拉角表示法的万向锁问题，也不像旋转矩阵 一样存在过多的冗余，是在姿态解算中常用的一种表示方法。

参考文献

[1] 黄耀聪.基于 IMU 的机器人位姿示教技术研究[D].广州：广东工业大学，2021.

本文只供大家参考与学习，谢谢！