用面积法解决 乐团站位 （29）

Posted 2022-11-30 Heisenberg_Posion

题目描述

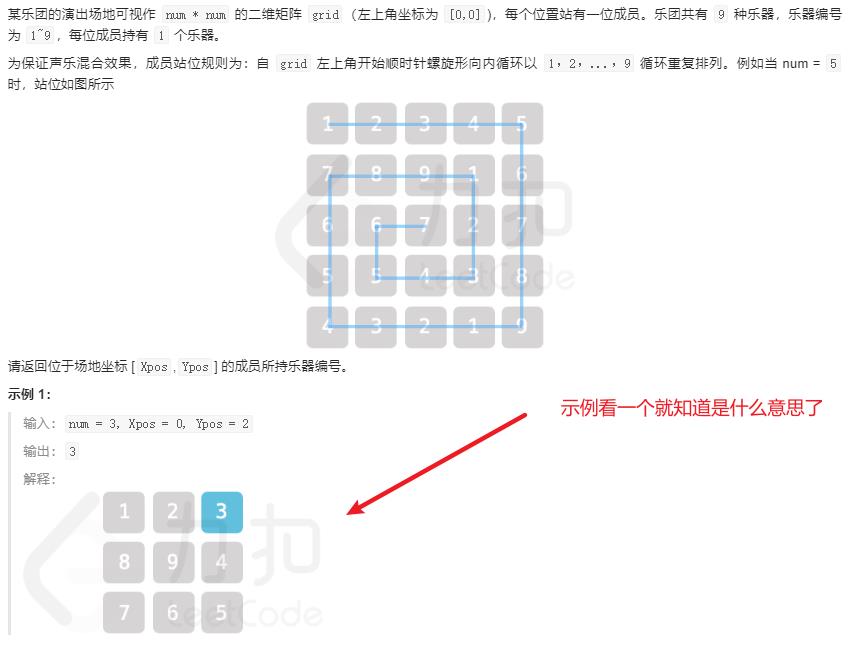
首先看这个题目真的是毫无下手之力，直到看到一个比较秒的解法，才让我搞懂这个题目怎么做。

题目解法
先确定圈数是(num+1)/2，确定要找的数在第几圈，这个的确定是通过比较 行号，列号，num-行号，num-列号，找到他们的最小值，即是在第几圈，这是看离四边哪边最近。
最外圈面积-所在圈的面积=外面所有元素的个数。
再模9+1就能得到所在圈得左上角得那个数。
最后再判断在圈的哪一边，最后就能计算得出要求的值。
怎么判断看代码就懂了，判断写代码的时候得是if else if else if ，不要写成了全部都是if ，程序会出错，一开始我就犯了这个错误，调试之后才发现出来。

/*某乐团的演出场地可视作 num* num 的二维矩阵 grid（左上角坐标为[0, 0])，每个位置站有一位成员。乐团共有 9 种乐器，乐器编号为 1~9，每位成员持有 1 个乐器。

为保证声乐混合效果，成员站位规则为：自 grid 左上角开始顺时针螺旋形向内循环以 1，2，...，9 循环重复排列。*/

#include<iostream>
using namespace std;

class Solution 
public:
    int orchestraLayout(int n, int xPos, int yPos) 
        long num = n;  //得将n转成long型,不然后面都无法表示。
        int numCircle = (num + 1) / 2;  //圈数
        int listCircle =min(min((long)xPos, (long)yPos), min(num-xPos-1,num-yPos-1))+1;  //要求元素所在的圈数
        long lenthIn = (num - (listCircle - 1) * 2) ;  //所在圈的边长;
        long areaIn = lenthIn * lenthIn;  //所在圈的面积
        long areaOut = num * num;  //总面积
        long index = (areaOut - areaIn) % 9 + 1; //圈内左上角的元素大小
        int left = listCircle - 1, right = num - listCircle;  //获取圈内的左边界和右边界
        //现在只需要判断这个要求的数在这个圈的哪条边
        if (xPos == left)    //在最上边
        
            index = (index + yPos - left) % 9;
        
        else if (yPos == right)    //在右边
        
            index = (index + right - left + xPos - left) % 9;
        
        else if (xPos == right)   //在最下边
        
            index = (index + (right - left) * 2 + right - yPos) % 9;
        
        else if (yPos == left)//在最左边
        
            index = (index + (right - left) * 3 + right - xPos) % 9;
        
        return index == 0 ? 9 : index;
    
;
int main()

    Solution s1;
    int resault = 0;
    resault = s1.orchestraLayout(3,0,2);
    cout << "the ansert is:"<<resault << endl;
	return 0;