AcWing86：链表中环的入口结点

Posted 2022-11-30 劭兮劭兮

今天不晒老婆了，晒晒最近很喜欢的向日葵和麦穗图，好美！

问题

原题链接：
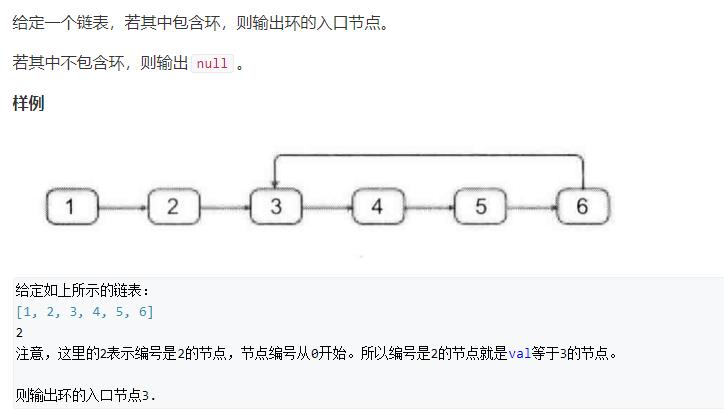
链表中环的入口结点

解决办法

链表快慢指针扫描

• 本题用first（慢指针），second（快指针）分别从起点走，first每次走一步，second每次走两步；
• 如果在此过程中，second走到空结点的地方，则不存在环，可返回null；
• 当first走了 x 到b点时，second已经在环上走了 x ，此时顺时针距离b点还有y；

那么为什么距离b点还有y呢？

• 如果第一次相遇的时候，如下情况：
  
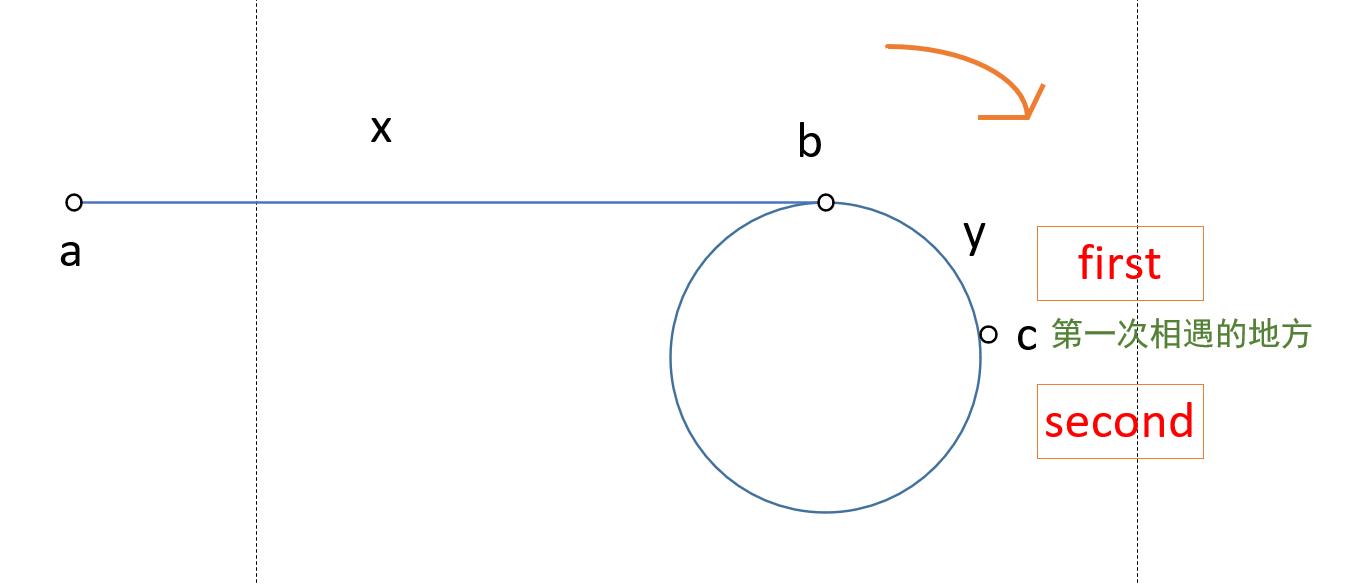
  （a 是起点，b 是环的入口，c 是两个指针的第一次相遇点，ab 之间的距离是 x，bc 之间的距离是 y)

当第一次相遇的时候，相遇在 c 点，first 走了 x + y ，second 走了 2(x + y)；

如果让first退回到 b 点，退了 y ，则 second 退了 2y ，即 此时 second 距离 b 点还有 y 的位置（如果要相遇，second 至少要比 first 多走一圈），也就是说，当 first 在 b 点时，x 在环上走了x , second 距离 b 点还有 y 的距离，这样才有了第一次相遇；

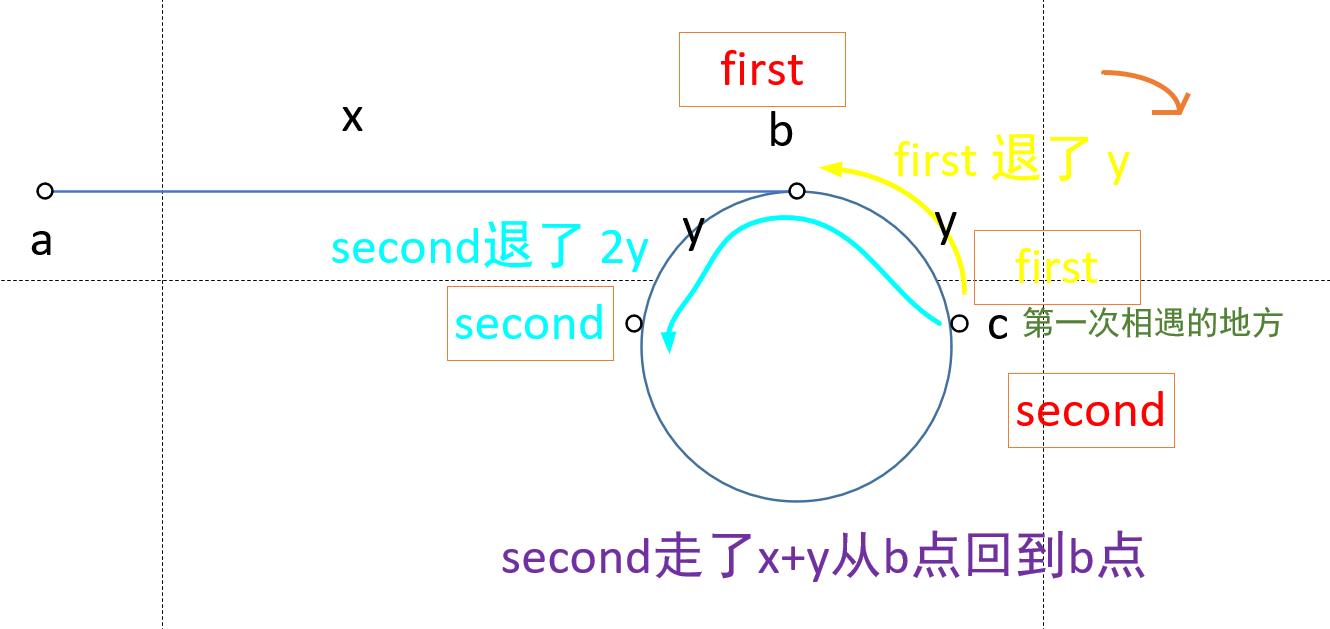
即，second走了 x+y 从 b 点回到 b 点；

• 如果 此时让 first 从 起点走 x 到 b 点，则 second 从 c 点顺时针走 x 也会回到 b 点，即第二次相遇的 点为 b 点，即 环的 入口点；

拓展：用公式证明

用 z 表示从 c 点顺时针走到 b 的距离；

• 则第一次相遇时 second 所走的距离是 x+(y+z)∗n+y, n 表示圈数;
• 同时 second 走过的距离是 first 的两倍，也就是 2(x+y)；
• 所以有 x+(y+z)∗n+y=2(x+y)，所以 x=(n−1)×(y+z)+z；
• 那么我们让 second 从 c 点开始走，走 x 步，会恰好走到 b 点；
• 让 first从 a 点开始走，走 x 步，也会走到 b 点；
• 第二次相遇在 b 点，即环的入口点；
  

JAVA代码实现

/**
 * Definition for singly-linked list.
 * class ListNode 
 *     int val;
 *     ListNode next;
 *     ListNode(int x) 
 *         val = x;
 *         next = null;
 *     
 * 
 */
class Solution 
    // public ListNode entryNodeOfLoop(ListNode head) 
        
    // 
    
    public ListNode entryNodeOfLoop(ListNode head) 
        
		if(head == null || head.next == null) 
			return null;
		
		
//		慢指针
		ListNode first = head;
//		快指针
		ListNode second = head;
		
		while(first!= null && second != null) 
//			慢指针一次走一步
			first = first.next;
//			快指针一次走两步，在此过程中，如果second走到空的结点，则没有环
			second = second.next;
			if(second.next != null) 
				second = second.next;
			else 
				return null;
			
			
//			第一次相遇
			if(first == second) 
				first = head;
				
//				第二次相遇的地方即为环的入口点
				while(first != second) 
					first = first.next;
					second = second.next;
				
				return first;
			
			
		
		
		return null;
		
		
    

小记：
原题链接：
链表中环的入口结点