算法和数据结构解析-4 : 字符串问题讲解

Posted 2022-11-30 鮀城小帅

1. 简介

字符串（String）是由零个或多个字符组成的有限序列，它是编程语言中表示文本的数据类型。

字符串与数组有很多相似之处，比如可以使用索引（下标）来得到一个字符。字符串，一般可以认为就是一个字符数组（char array）。不过字符串有其鲜明的特点，它的结构相对简单，但规模可能是非常庞大的。

在编程语言中，字符串往往由特定字符集内有限的字符组合而成。在 Java 中字符串属于对象，Java 提供了 String 类来创建和操作字符串。

2. 字符串相加（来源：力扣（LeetCode））

2.1 题目说明

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和并同样以字符串形式返回。

提示：

1. num1 和num2 的长度都小于 5100
2. num1 和num2 都只包含数字 0-9
3. num1 和num2 都不包含任何前导零
4. 你不能使用任何內建 BigInteger 库， 也不能直接将输入的字符串转换为整数形式

2.2 分析

这里不允许直接将输入字符串转为整数，那自然想到应该把字符串按每个字符char一一拆开，相当于遍历整数上的每一个数位，然后通过“乘10叠加”的方式，就可以整合起来了。这相当于算术中的“竖式加法”。

另外题目要求不能使用BigInteger的内建库，这其实就是让我们自己实现一个大整数相加的功能。

 2.3 代码实现

    public String addStrings(String num1, String num2) 
        // 定义一个StringBuffer，保存最终的结果
        StringBuffer stringBuffer = new StringBuffer();
        // 定义遍历两个字符串的初始位置
        int i = num1.length() - 1;
        int j = num2.length() - 1;
        int carry = 0;

        // 从个位开始遍历，只要还有数没计算完，就继续计算，其他数补0
        while ( i >= 0 || j >= 0 || carry != 0 )

            // - ‘0’ 是因为字符要将ascii码转换为数字
            int n1 = i >= 0 ? num1.charAt(i) - '0' : 0 ;
            int n2 = j >= 0 ? num2.charAt(j) - '0' : 0 ;

            // 对当前数位求和
            int sum = n1 + n2 + carry;

            // 把sum的个位数保存到结果中，十位数作为进位保存下来
            stringBuffer.append(sum % 10);
            carry = sum / 10;

            // 移动指针，继续遍历下一位
            i --;
            j --;
        
        return stringBuffer.reverse().toString();
    

2.4 复杂度分析

时间复杂度：O(max(len1,len2))，其中len1 =num1.length，len2 =num2.length。竖式加法的次数取决于较大数的位数。

空间复杂度：O(n)。解法中使用到了 StringBuffer，所以空间复杂度为 O(n)。

3. 字符串相乘（#43）

3.1 题目说明

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

示例 1:

输入: num1 = "2", num2 = "3"

输出: "6"

示例 2:

输入: num1 = "123", num2 = "456"

输出: "56088"

说明：

1. num1 和 num2 的长度小于110。
2. num1 和 num2 只包含数字 0-9。
3. num1 和 num2 均不以零开头，除非是数字 0 本身。
4. 不能使用任何标准库的大数类型（比如 BigInteger）或直接将输入转换为整数来处理。

3.2 分析

跟“字符串相加”类似，这里我们要处理的，也是大整数的相乘问题。

思路也可以非常类似：我们借鉴数学中“竖式乘法”的规则，用num1分别去乘num2的每一位数字，最后再用AddStrings将乘出的结果全部叠加起来就可以了。

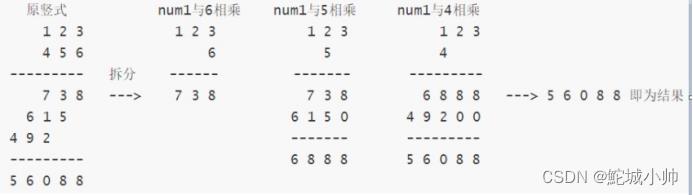
 3.3 代码

     public String multiply(String num1, String num2) 

        if( num1.equals('0')  || num2.equals('0') )
            return "0";
        
        // 定义输出结果，直接定义为String，调用字符串相加方法
        String result = "0";

        // 从各位开始遍历num2的每一位，跟num1相乘，并叠加计算结果
        for (int i = num2.length() - 1; i >= 0; i--)
            // 取出num2的当前位数，作为当前乘法的第二个乘数
            int n2 = num2.charAt(i) - '0';
            // 用一个StringBuffer保存乘积结果
            StringBuffer curRes = new StringBuffer();
            int carry = 0;

            // 因为结果是倒叙的，所以当前n2对应数位要补0，应该先写入curResult，补n-1-i个0（比如当前为十位，那么个位要补0）
            for (int j = 0; j < num2.length()-1-i; j++)
                curRes.append("0");
            
            // 从个位开始遍历num1中的每一位，与n2相乘，并叠加
            for (int j = num1.length() - 1 ; j >= 0; j-- )
                // 取出num1的当前数位，作为当前乘法的第一个乘数
                int n1 = num1.charAt(j) - '0';
                // 计算当前数位的乘积结果
                int product = n1 * n2 + carry;

                curRes.append(product % 10);
                carry = product / 10;
            

            // 3. 所有数位乘法计算完毕，如果有进位，需要将进位单独作为一位保存下来
            if(carry != 0) curRes.append(carry);
            // 4. 将当前乘积叠加到result中
            AddStrings addStrings = new AddStrings();
            result = addStrings.addStrings(result,curRes.reverse().toString());
        
        return result;
    

3.4 复杂度分析

时间复杂度：O(mn+n^2)，其中 m 和 n 分别是 num1 和 num2的长度。

做计算的时候，外层需要从右往左遍历num2，而对于num2的每一位，都需要和 num1的每一位计算乘积，因此计算乘积的总次数是 mn。字符串相加操作共有 n次，每次相加的字符串长度最长为 m+n，因此字符串相加的时间复杂度是 O(mn+n^2)。总时间复杂度是 O(mn+n^2)。

空间复杂度：O(m+n)。空间复杂度取决于存储中间状态的字符串，由于乘积的最大长度为 m+n，因此存储中间状态的字符串的长度不会超过 m+n。

3.5 算法优化

我们看到计算过程中，用到了太多的字符串相加操作，调用addStrings方法时又需要遍历字符串的每一位，这个过程显得有些繁琐。能不能用其它的方法进行简化呢？

我们发现，m位数乘以n位数，结果最多就是m+n位；所以我们可以用一个m+n长度的数组来保存计算结果。

而且，某两个数位相乘，num1[i] x num2[j] 的结果(定义为两位数，一位数的话前面补0)，其第一位位于 result[i+j]，第二位位于 result[i+j+1]。

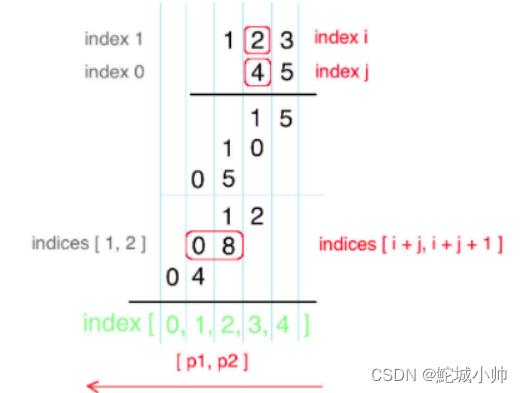
根据上面的思路，我们可以遍历num1和num2中的每一位数，相乘后叠加到result的对应位上就可以了。

    public String multiply2(String num1, String num2) 

        if( num1.equals('0')  || num2.equals('0') )
            return "0";
        
        // 定义一个数组，保存计算结果的每一位
        int[] resultArr = new int[ num1.length()  * num2.length()];

        // 遍历num1和num2的每个数位，做乘积，然后找到对应数位，填入结果数组
        for (int i = num1.length() -1 ; i >=0 ; i--)
            int n1 = num1.charAt(i) - '0';
            for (int j = num2.length() -1 ; j >= 0; j--)
                int n2 = num2.charAt(j) - '0';

                // 计算乘积
                int product = n1 * n2;

                // 保存到数组
                int sum = product + resultArr[i+j+1];
                resultArr[i+j+1] = sum % 10;  // 叠加结果的个位保存到i+j+1
                resultArr[i+j] = sum / 10;
            
        

        // 将结果数组转为String输出
        StringBuffer buffer = new StringBuffer();
        int start = resultArr[0] == 0 ? 1 : 0;
        for (int index= start; index < resultArr.length;index++)
            buffer.append(resultArr[index]);
        
        return result;
    

复杂度分析

时间复杂度：O(mn)，其中 m 和 n 分别是 num1 和 num2的长度。需要计算num1 的每一位和 num2的每一位的乘积。

空间复杂度：O(m+n)，需要创建一个长度为 m+n 的数组存储乘积。

4. 去除重复字母

4.1 题目说明

给你一个字符串 s ，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证 返回结果的字典序最小（要求不能打乱其他字符的相对位置）。

示例 1：

输入：s = "bcabc"

输出："abc"

示例 2：

输入：s = "cbacdcbc"

输出："acdb"

提示：

1. 1 <= s.length <= 104
2. s 由小写英文字母组成

4.2 分析

首先要知道什么叫 “字典序”。

字符串之间比较跟数字之间比较是不太一样的：字符串比较，是从头往后一个字符一个字符比较的，哪个字符串大取决于两个字符串中第一个对应不相等的字符。

所以，任意一个以 a 开头的字符串都大于任意一个以 b 开头的字符串。

为了得到最小字典序的结果，解题过程中，我们可以将最小的字符尽可能的放在前面，把前面出现的重复字母全部删除。这其实就是一个贪心策略。

4.3 方法一：贪心策略（逐个字符处理）

    /**
     * 方法一：暴力法，贪心策略递归
     * @param s
     * @return
     */
    public String removeDuplicateLetters(String s) 
        // 递归的基准情形
        // 如果字符串为空串，直接返回
        if (s.length() == 0) return "";

        // 希望找到当前最左侧的字母，位置记为position
        int position = 0;

        // 遍历字符串
        for (int i = 0; i < s.length(); i++)

            // 这里从 i 之前开始遍历是否存在重复元素
            // 只有当前字母比已经找到的position位置的字母要小，才有资格继续判断。
            // 比如： ab时，i=1,position=0,此时，i(b)>position(a)，是按照字典的顺序增长，不需要进行判断
            if(s.charAt(i) < s.charAt(position))
                // 定义一个布尔变量，表示j位置的字母是否重复出现
                boolean isReplaceable = true;

                // 遍历i之前的所有字母，判断是否在i后面重复出现
                for (int j = position; j < i; j++)
                    // 定义一个布尔变量，表示j位置的字母是否重复出现
                    boolean isDuplicated = false;
                    // 遍历i后面的所有字母，看j位置的字母是否重复出现.
                    for (int k = i + 1 ; k < s.length(); k ++)
                        if (s.charAt(j) == s.charAt(i))
                            isDuplicated = true;
                            break;
                        
                    
                    // 如果任一字母不重复出现，就不能替换当前position，后面的字母不用判断
                    if (!isDuplicated)
                        isReplaceable = false;
                        break;
                    
                
                if (isReplaceable) position = i;
            
        
        // 遍历结束，position位置的字母就是结果中最左侧的元素
        return s.substring(position) + removeDuplicateLetters(s.substring(position+1).replaceAll(s.charAt(position)+"",""));
    

复杂度分析

1. 时间复杂度：O(N^3)，因为用到了三重循环，最坏情况下时间复杂度达到了N^3。（超出运行时间限制）
2. 空间复杂度：O(N)，每次给字符串切片都会创建一个新的字符串（字符串不可变），切片的数量受常数限制，最终复杂度为 O(N) * C = O(N)。

4.4 方法二：贪心策略改进

我们发现，对于“是否重复出现”的判断，每次都要偏离当前字母之后的所有字符，这显然做了很多重复工作。

优化的方法，我们可以用一个count数组，保存所有26个字母在s中出现的频次。当我们遍历字符串时，每遇到一个字母，就让它对应的count减一；当当前字母对应的count减为0时，说明之后不会再重复出现了，因此即使有更小的字母也不能替代它，我们直接就可以把它作为最左侧字母输出了。

    /**
     * 方法二：贪心策略改进
     * @param s
     * @return
     */
    public String removeDuplicateLetters2(String s) 
        // 递归的基准情形
        // 如果字符串为空串，直接返回
        if (s.length() == 0) return "";

        // 定义一个count数组，保存所有26个字母在字符串中出现的频次
        int[] count = new int[26];

        for (int i = 0; i < s.length(); i++) 
            // count[0]保存a的个数；count[1]保存b的个数
            count[ s.charAt(i) - 'a']++;
        

        // 希望找到当前最左侧的字母，位置记为position
        int position = 0;

        // 遍历字符串，找到当前最左端字母
        for (int j = 0; j < s.length(); j++) 

            // 每遇到一个字符，count值就要减1
            // 如果遇到count减为0，就直接退出，以当前最小的字母作为最左端字符
            if ( s.charAt(j) < s.charAt(position))
                position = j;
            
            // 把当前字符和position位置比较，如果更小就替换
            if ( --count[s.charAt(j) - 'a'] == 0)
                break;
            
        

        // 遍历结束，position位置的字母就是结果中最左侧的元素
        return s.substring(position) + removeDuplicateLetters2(s.substring(position+1).replaceAll(s.charAt(position)+"",""));
    

复杂度分析

1. 时间复杂度：O(N)。 每次递归调用占用 O(N) 时间。递归调用的次数受常数限制(只有26个字母)，最终复杂度为 O(N) * C = O(N)。
2. 空间复杂度：O(N)，每次给字符串切片都会创建一个新的字符串（字符串不可变），切片的数量受常数限制，最终复杂度为 O(N) * C = O(N)。

4.5 方法三：贪心策略（用栈实现）

    /**
     * 方法三：使用栈进行优化
     * @param s
     * @return
     */
    public String removeDuplicateLetters3(String s) 
        // 定义一个字符栈，保存去重之后的记过
        Stack<Character> stack = new Stack<>();

        // 为了快速判断一个字符是否在栈中出现过，用一个set来保存元素是否出现
        HashSet<Character> seenSet = new HashSet<>();

        // 为了快速判断一个字符是否在某个位置之后重复出现，用一个HashMap来保存字母出现在字符串的最后位置
        HashMap<Character,Integer> lastOccur = new HashMap<>();

        // 遍历字符串，将最后一次出现的位置保存进map
        for (int i = 0; i < s.length(); i++) 
            lastOccur.put(s.charAt(i),i);
        

        // 遍历字符串，判断每个字符串是否需要入栈
        for (int i = 0; i < s.length(); i++) 
            char c = s.charAt(i);
            // 只有在c没有出现过的情况下，才判断是否入栈
            if (!seenSet.contains(c))
                // c入栈之前，要判断当前栈元素，是否在后面会重复出现；如果重复出现就可以删除
                while ( !stack.isEmpty() && c < stack.peek() && lastOccur.get(stack.peek()) > i)
                    seenSet.remove(stack.pop());
                
                stack.push(c);
                seenSet.add(c);
            
        

        // 将栈中的元素保存成字符串输出
        StringBuilder str = new StringBuilder();
        for (Character character : stack) 
            str.append(character.charValue());
        

        return str.toString();
    

复杂度分析

时间复杂度：O(N)。虽然看起来是双重循环，但内循环的次数受栈中剩余字符总数的限制，因为栈中的元素不重复，不会超出字母表大小，因此最终复杂度仍为 O(N)。

空间复杂度：O(1)。看上去空间复杂度像是 O(N)，但实际上并不是。首先，seen 中字符不重复，其大小会受字母表大小的限制，所以是O(1)。其次，只有 stack 中不存在的元素才会被压入，因此 stack 中的元素也唯一。所以最终空间复杂度为 O(1)。