计算机视觉中的深度学习7: 卷积神经网络

Posted 2022-11-30 SuPhoebe

Slides：百度云 提取码: gs3n

之前说了全连接神经网络，说了线性分类，这些东西全都没有保留图片原本的2D特性，全都是将图片转化为1D的数组。

而今天说的CNN，则是能更好地保留图片的2D特性，在CV中有着更广泛地运用。

卷积层

对于一个32x32x3的一个图片，全连接层将它平摊成一个3072x1的数组

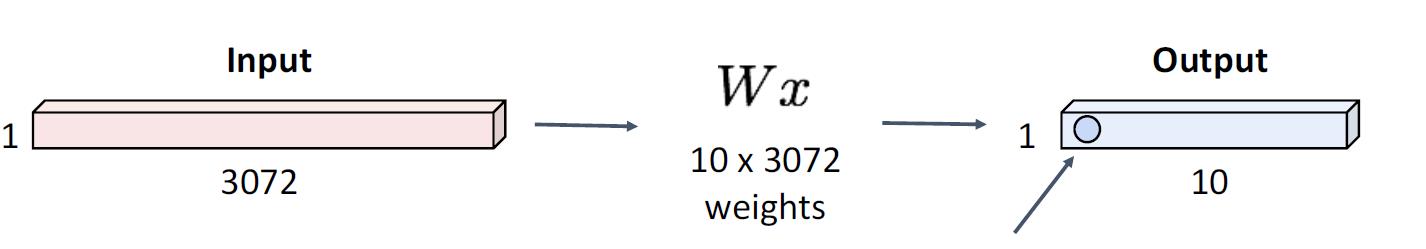
对于同样的图片，卷积层则是这么做的

它通过一个和输入图片同样高的filter，让filter与输入图片进行卷积，得出了一个28x28x1的新的图片

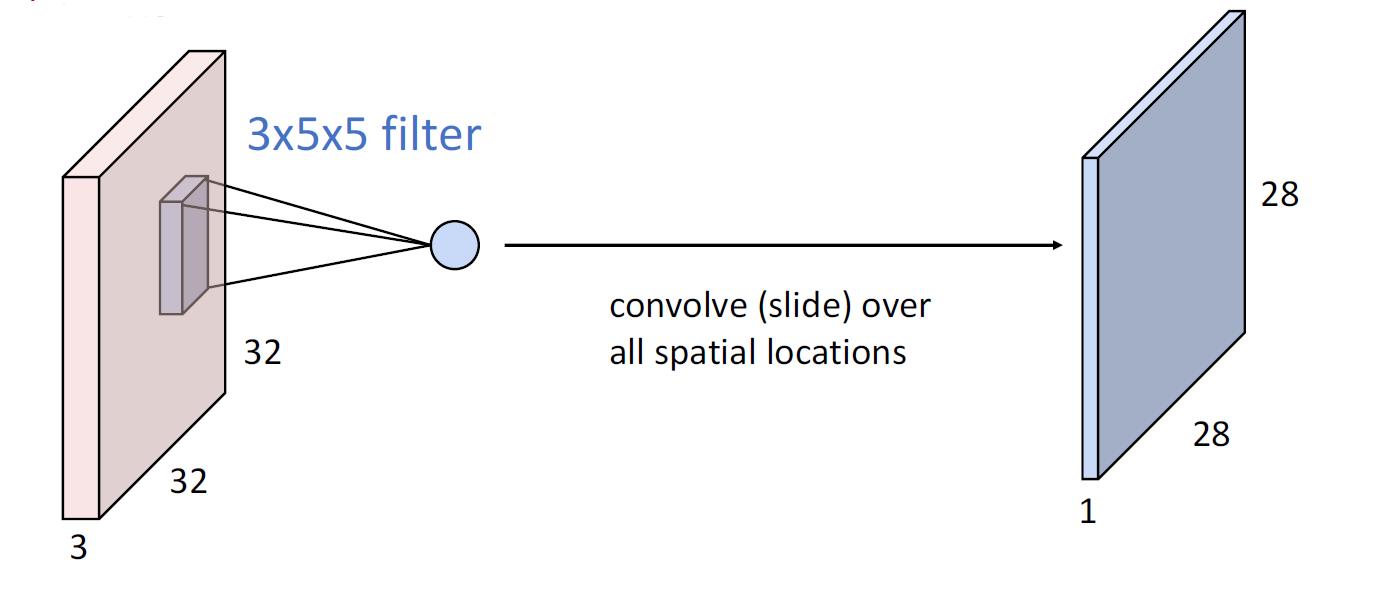
同时，我们可以有多个filter，从而产生多个输出图片

那么这儿共有6个filter，输出则是6组图像，你可以将这6组图像当做一个6x28x28的三维新图片

将其串联起来就是如下的结构

输入输出的大小关系

我们可以明显得看出来

1. 关于高度
   1. 输出的高度与输入的高度无关，只与filter的个数有关
   2. filter的高度和输入的高度一致
2. 关于长宽
   1. 输入的长W，filter长K，输出则为$W-K+1$
   2. 同理宽

我们可以看到经过多轮卷积层的处理，图片会越来越小，每次特征图片的处理都会损失更一些大小。这样可能会造成，对于一个太深的神经网络，处理到后期，图片就变成1x1的大小而无法被处理了。

Padding

在图片周围加入一些0

1. 关于长宽的计算
   1. 输入的长W，filter长K，padding大小P，输出则为$W-K+1+2P$
   2. 同理宽

一般来说，将其设置为$P=(K-1)/2$，这样输入和输出的大小就会一样。

将周围填充为0，并不是对图片特征提取完全没有帮助，它能够更好地处理图片边缘的情况，且明确地告诉网络，这个图片的每个特征处于图片的什么位置。

感受域

对于内核大小为K的卷积层，输出中的每个元素取决于输入中的K x K感受域

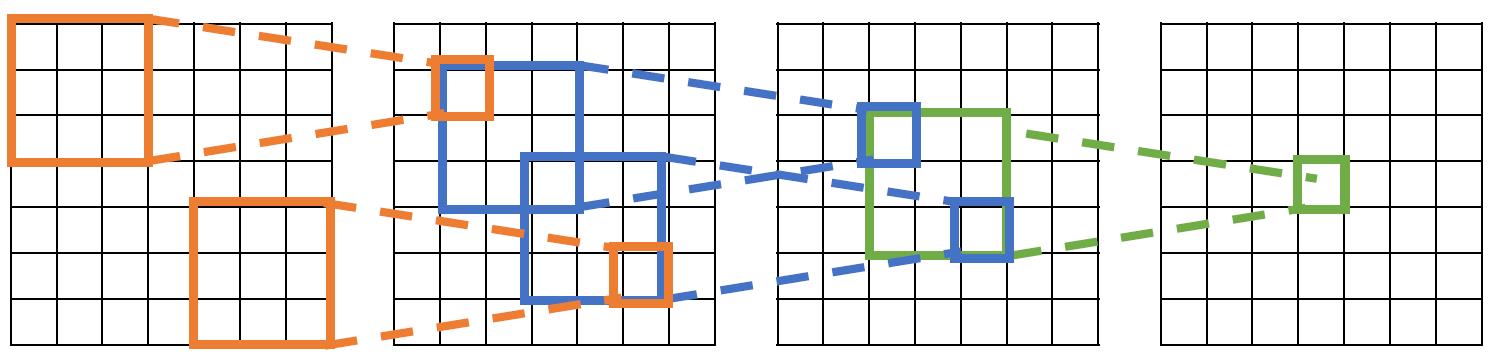
每次连续的卷积都会使感受域大小增加K – 1，对于L层，感受域大小为1 + L *（K – 1）。

这样的好处显而易见，它能让底层的图片特征能够全盘感受这张图片，例如，在左上角和右下角的区域，要通过多层卷积处理使得他们产生联系。

那么这样的问题也更显而易见，对于一些特别巨大的图片，往往需要很多很多层卷积才能让神经网络最终看到整张图片。

跳步卷积

对于之前的卷积，我们都是将filter一格一格移动的，但是这次我们是跳步进行的。假设步长为2，则我们将filter每一次卷积之后都要横向移动两位。

1. 关于长宽的计算
   1. 输入的长W，filter长K，padding大小P，跳步大小为S
      1. 输出则为$(W-K+2P)/S+1$
   2. 同理宽

这样我们就能更快地获得图片的全貌

总结

池层（Pooling Layers）

1. Pooling层是一种能更快提取特征的方式
2. 它能够将不变性引入一小块区域
3. 它没有可以训练的参数
4. 它能够通过非线性的方式提取特征

如下图所示，这就是一个2x2的max pooling
我想这是一个很好找规律的东西

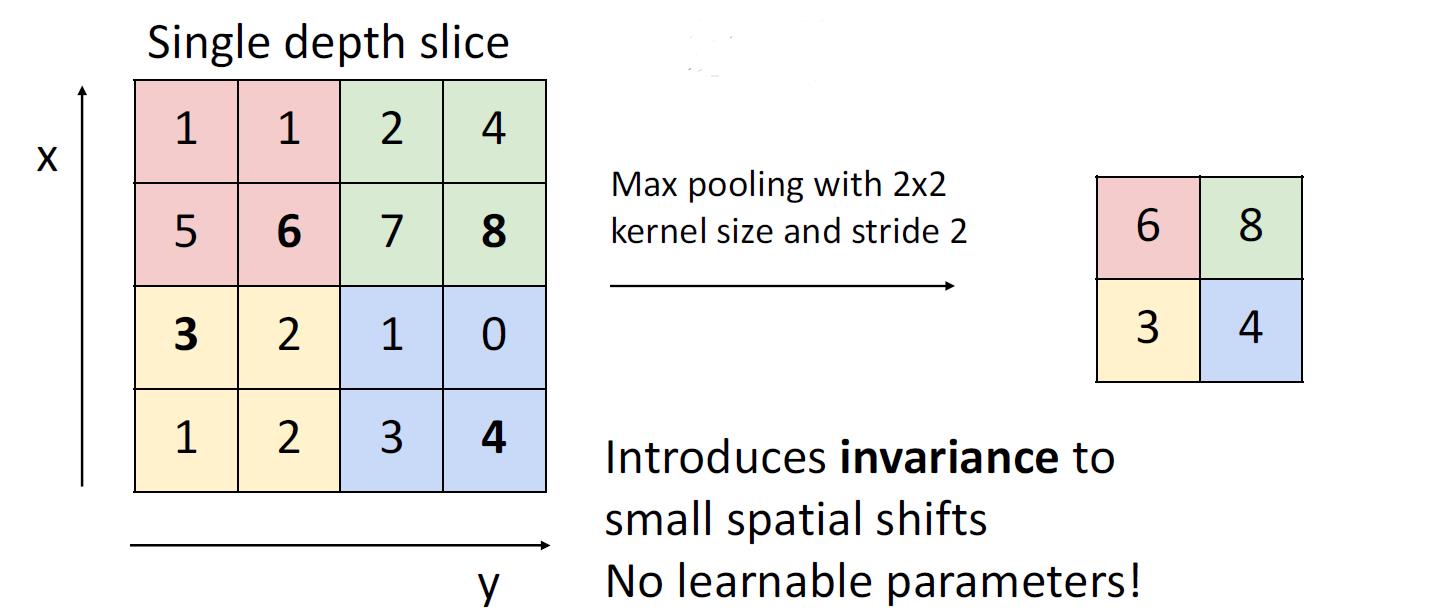
常用的pooling还有average pooling等

LeNet-5

用卷积神经网络检测脸部关键点的教程

批量归一化

想法：“归一化”层的输出，以便它们的均值和单位方差为零

原因：能够极大提高收敛效率，论文《Ioffe and Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift”, ICML 2015》

做法：
对于一个批量的输入，我们可以这样

输入$x:N\times D$
可以学习的参数$\gamma ,\beta :D$
对于$\gamma ,\beta$，他们与x的函数如下

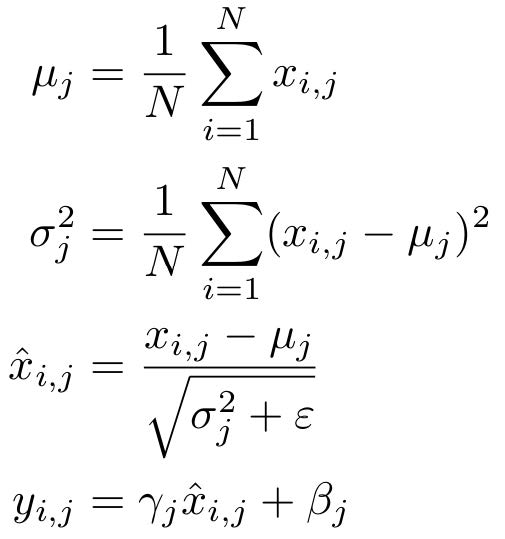
你可以发现，这会是一个线性的变化。

Test的情况下

我们会发现，在test的情况下，我们并没有批量的输入，所以我们也没法维持$\mu$和$\sigma$。那么这将会使得我们的归一化失败。

于是，我们就应该将${\mu }_{t}est$和${\sigma }_{t}est$设置成为，在训练时的$\mu$和$\sigma$的平均数。

在测试期间，批量归一化成为线性运算！可以与先前的全连接层或转换层融合

好处

• 使深层网络更容易训练！
• 允许更高的学习率，更快的收敛
• 网络对初始化变得更加健壮（robust）
• 在训练期间充当正则化
• 测试时零开销：可以与卷积层完美融合！