人工智能基于八数码问题对比搜索算法的性能
Posted 张牧之!
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工智能基于八数码问题对比搜索算法的性能相关的知识,希望对你有一定的参考价值。
基于八数码问题对比搜索算法的性能
摘要:八数码问题是人工智能的一个经典问题,以宽度优先搜索、深度优先搜索以及A* 算法求解八数码问题。每一种算法都设置相同的初始状态和目标状态,针对搜索策略,求得问题的解,并比较搜索算法的性能以引导分析出更高效的搜索算法策略。
关键词:搜索算法;深度优先搜索算法;宽度优先搜索算法;八数码问题;A*算法;
0 引言
搜索算法实际上是根据通过初始条件和初始条件之间实现扩展的规则来形成构建成一棵“树”,所以在查找目标状态下的节点过程中也就类似于图,或者是树的遍历过程。但每种搜索算法的实现方法中也同样应该包括了控制节点(扩展节点的方式)和产生系统(扩展节点)。一般在大规模的搜索试验中,通常可以采用在一次搜索之前,根据实验条件要求减小每一次搜索量的规模。又或者利用每一个问题的实际约束值和条件,用来实现进行搜索剪枝。也可以利用搜索过程对其中的中间值计算,避免重复搜索计算来实现搜索引擎的优化。
笔者在求解八数码经典问题时分别使用这三种算法进行实验测试,通过实验结果分析三种算法的特点与性能以引导分析出更高效的搜索算法策略。
1问题描述
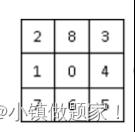
八数码问题指的是在三行三列的构建的一个棋盘中,摆放有八个方块,将八个方块摆放在棋盘的不同方格中,每个方块不能摆放在同一个方格中,并且在棋盘中留有一个空白方格不放入方块。之后在每个方块上写上一到八的其中的一个阿拉伯数字。允许其附近周围相邻的方格中的方块可以向未放入方块的空白方格进行移动。要解决的基本问题是:利用移动围盘中的所有方格,寻找找一个可以从初始状态转换为目标状态的移动方块步骤数中的最小的移动步骤。而求解八数码问题,实际上是找出从初始状态到目标状态之间,所经过的一种最合理的中间转换状态。
例如如图1是八数码的一个初始状态和目标状态

2 三种搜索算法的概述
2.1宽度优先(BFS)
在具体的实现中,使用open和closed两个表[4],open表是一个队列,每次对open表进行一次出队操作(并放入closed表中),并将其邻居节点进行入队操作。直到队列为空时即完成了所有节点的遍历。closed表在遍历树时其实没有用,因为子节点只能从父节点遍历到达。但在进行图的遍历时,一个节点可能会由多个节点到达,所以此时为了防止重复遍历应该每次都检查下一个节点是否已经在closed表中了。
以数字零为研究对象,由此可知在每一步移动中,数字零的移动方向可能有左、上、下、右四个方向。在扩展节点时需要判断数字零是否能往上、下左、右这四个方向移动。通过分析可知,如果该节点是通过其父节点中数字零向左(上、下、右)移动得到的,则在扩展该节点时数字零不能向右(下、上、左)移动,即通过该节点扩展出来节点是否保留的条件是扩展出来的节点是否与其父节点的父节点相同,若不相同则保留,否则舍去。然后判断每次扩展出来的节点中是否有目标节点,如果有目标节点则停止扩展节点、输出结果路径,否则将扩展的节点加入到open表的末端。
基本步骤
(1)建立含有一个只含有初始节点S的搜索图G,然后把该节点移入open表中。
(2)建立closed表,其初始值为空表。
(3)如果open表是空表,则失败直接退出即可。
(4如果选择了当前open列表中一个起始节点,并将它从当前的open列表中删除并重新放入当前的closed列表中,则称此节点为当前节点。
(5)如果当前节点为目标节点,则找到解并直接退出即可。
(6)扩展当前节点,并把子节点放到open表的后面即可。
实验算法流程
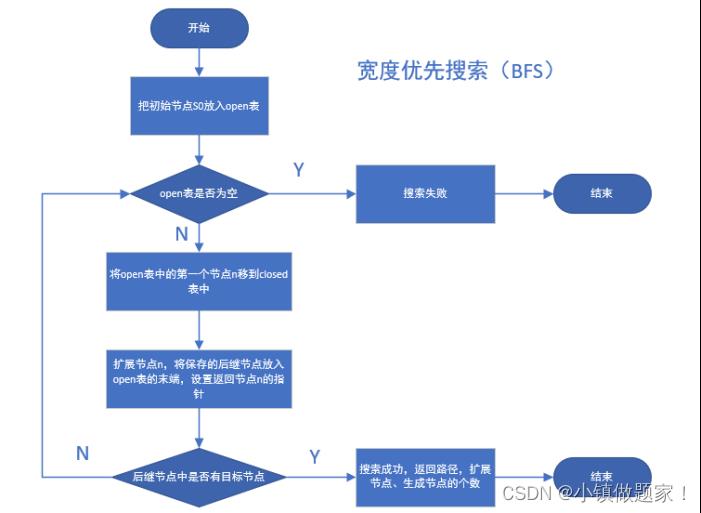
2.2 深度优先(DFS)
深度优先搜索算法在求解八数码问题的过程中在节点扩展时的方法与宽度优先搜索一样,但唯一不同的是深度优先搜索扩展出来的节点中如果没有目标节点则会把这些节点加入到open表的开始前端。
为了防止搜索过程中扩展出来更多不具有益处的节点,所以我们可以设置一个扩展最大深度maxdepth,如果搜索过程中存在节点已经超过我们设置的最大深度则我们需要舍弃这些扩展出来的节点,视为没有这些节点没有后继节点,就不需要往后进扩展了。
基本步骤
(1)建立一个只含有初始节点S的搜索图G,然后把该节点移入open表中。
(2)建立closed表,其初始值为空表。
(3)如果open表是空表,则失败直接退出即可。
(4)如果选择了当前open列表中一个起始节点,并将它从当前的open列表中删除并重新放入当前的closed列表中,则称此节点为当前节点。(5)如果当前节点为目标节点,则找到解并直接退出即可。
(6)扩展当前节点,并把子节点放到open表的前面即可。
实验算法流程
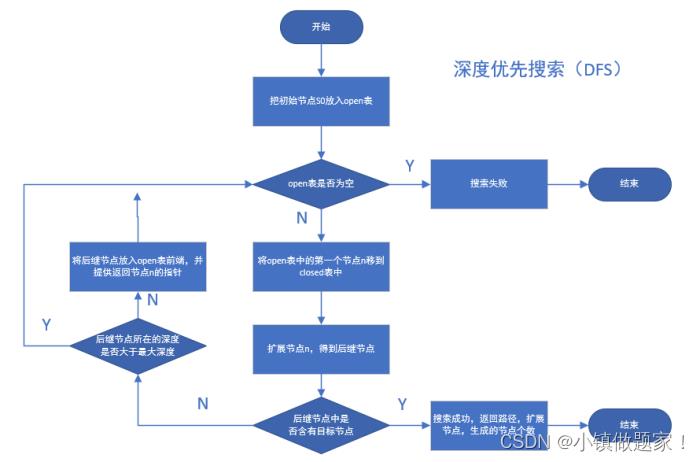
2.3 A*算法
A* 算法是一种对求解最短路径问题最有效的搜索计算方法,也是许多其他问题的常用启发式算法。
A* 的启发函数[1]为f(n)=g(n)+h(n)
f(n)[1]是从初始状态经由状态n到目标状态代价估计,g(n)是在状态空间中从初始状态到状态n的实际代价,h(n)是状态空间n到目标状态的最佳路径的估算代价。
A* 算法在扩展节点时的方法与宽度、深度优先搜索算法一致。唯一不同的是A*算法根据启发函数的信息对open表进行重排,这样做大大减少了对无用节点的扩展。对open表进行重排指的是按照估价函数h(n)的值从小到大的估价顺序重排open表中每个节点的顺序。这样可以保证每一次扩展的节点都是open表中有用的节点。
基本步骤
(1)建立一个只含有初始节点S的搜索图G,然后把该节点移入open表中。
(2)建立closed表,其初始值为空。
(3)如果open表是空表,则失败直接退出即可。
(4)按照预先定义的估价函数从小到大的顺序重新排列open表;
(5)如果选择了当前open列表中一个起始节点,并将它从当前的open列表中删除并重新放入当前的closed列表中,则称此节点为当前节点。
(6)如果当前节点为目标节点,则找到解并直接退出即可。
(7)否则返回步骤(3)循环进行后续操作。
实验算法流程

3 基于八数码问题实验测试
变量含义
生成节点数:生成节点数指的是在解决实际问题的过程中,统计总共生成的节点数量,侧面反映了用于解决实际问题中算法的时间和空间复杂度的优劣性。
扩展节点数:而在处理实际问题的过程中,所选择进行拓展的节点数量,从侧面体现了它在处理实际问题过程中算法启发能力等方面的优秀度,在实验检测中则用了拓展节点数的数据化表征。
测试数据1
宽度优先、深度优先、A*算法对测试数据1最终返回的路径图如下图 所示

测试数据1结果统计图
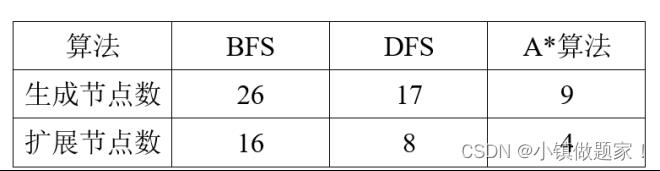
对比实验测试结果分析可知,当从初始状态到目标状态所能达到的最短距离比较小时,三种算法进行实验操作的过程中均能找到实验结果的最短路径,但是其中A* 算法不仅可以快速找到实验结果的最短路径,而且A*算法可以能够大大减少无用节点的扩展,减少在搜索过程空间的占用。
测试数据2

宽度优先、A*算法最终返回的路径图如图所示

深度优先最终返回的路径图如图所示

测试数据2结果统计图

对比实验测试结果可知,当从初始状态到目标状态所能达到的最短距离较大时,使用bfs算法与A* 算法进行实验的操作过程中可以能够找到这条最短路径,而使用dfs算法在实验的操作过程中却没有找到实验结果的最短路径,并且dfs算法在搜索的过程中造成较大的资源的浪费。所以对比三种算法,可以分析出A* 算法仍然是bfs算法与dfs以及A* 算法中三种算法中最节省资源的搜索方法。
测试数据3

测试数据3结果统计图

对比实验测试结果可知,当从初始状态到目标状态所能达到的最短距离较大时,A* 算法在实验操作的过程中可以能够找到实验结果的最短路径,而bfs算法与dfs算法在实验操作的过程中却没有找到实验结果的最短路径,并且造成较大的资源浪费,对比三种实验结果,可以分析出A* 算法仍然是bfs算法与dfs算法以及A* 算法三种算法中最节省资源的搜索方法。
4基于八数码问题对三种搜索算法的性能分析
通过分析试验结果,可分析出三种搜索算法在解决八数码问题的时候的优缺点。从宽度优先搜索算法、深度优先搜索算法、A* 算法三个搜索算法总的来说,宽度优先搜索算法和深度优先搜索算法,都是一个和实际具体问题无关的普通的搜索算法,对一般的实际问题,在通过这二个算法进行处理时,也都能够进行实际应用。针对于实际搜索问题,通过深度优先查找通常无法完全确保能够找出最好的解, 而如果在最坏情况时,则深度优先搜索的过程就相当于一个穷举的过程。同时,为了解决在搜索过程中沿着最无用的路径不断延伸的问题,还必须设定每一个节点可以扩展的最大深度,而超过了最大深度的节点也将被看作没有后继节点。所以可能会发生实际问题的解出现在设置的最大深度以外,也是不能够发现目标节点。宽度优先搜索在实验的测试中是可以得到实验结果的最优解,但是由于宽度优先搜索在搜索的过程中进行了扩展节点,并且扩展了大量的节点,所以对每个新产生的节点要确定是否为新节点,并且会耗费了大量的空间和时间,因为宽度优先搜索需要对已产生的节点进行遍历和比较。而A* 算法就可以解决宽度优先搜索算法和深度优先搜索算法在求解实际问题中存在的不足之处[3]。所以,每个新生成的节点在确定是否为全新节点时都需要对已经创建的新节点进行遍历和比较,耗费了大量的空间和时间。而A* 算法就能够克服了宽度优先搜索算法和深度优先搜索算法在解决实际问题过程中出现的缺陷。A* 算法的最大优点,就是在搜寻的过程中不管从时间上或者空间上,都可以进行了很好的优化处理。而启发式搜寻则是通过在状态空间中的搜索过程对每一次搜寻的方法进行代价评估,得出最佳的地方然后在这个地方进行搜寻直到目标。
A* 算法求解实际问题过程中扩展最少的节点,最快地找到最优解,但如果评估函数选得不好,会影响效率。在本次使用A* 算法求解八数码问题的实验测试过程中,笔者使用的是曼哈顿距离。但是在完成实验测试操作结束后,笔者使用曼哈顿距离、欧式几何平面距离和切比雪夫距离[2],同样测试本次实验中的三组相同的数据,并且对于实验测试结果进行分析。
测试数据1实验结果
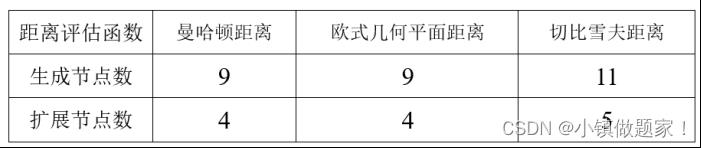
测试数据2实验结果
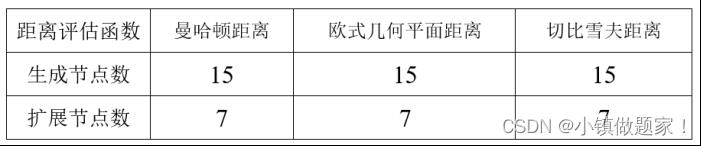
测试数据3实验结果

经过分析实验测试结果可知,距离评估函数同样影响的启发式搜索(A* 算法)的搜索效率,因为距离评估函数影响着h(n)值的大小,侧面的反映了曼哈顿距离在求解八数码问题中可以提高A* 算法的搜索效率。
5 研究结论
分析大量的搜索实验的数据测试结果之后,笔者可以总结并得出得出相应的实验结论, 宽度优先搜索最大的优点之处在于能够保证找到实际问题的解,不过也因为由于在搜索的进行过程中必须需要存储大量的状态信息而会导致空间复杂度相当的大,从而容易产生“组合爆炸”的问题。深度优先搜索最大优点之处就是有时候程序会比较快地找到实际问题的解,不过如果不能使用回溯优化,找到的解可能不是实际问题的最优解,而且如果限定了其搜索的最大深度或者持续的时间,就有可能找不出实际问题的解法。A* 算法是一种启发式的搜索,A* 算法实现的过程中在搜索的过程中也需要保存一些搜索的状态,但是由于A* 算法在搜索的过程中能够在每次进行扩展的时候有启发地选择了有最优的节点进行扩展,因此从局部最优推至全局最优,大大的缩小了搜索的时间复杂度和空间复杂度,并且使用A* 算法在求解实际问题过程中快速的找到最优解。
搜索算法研究作为当前人工智能大量应用算法中一个重要的研究应用领域,在信息科技迅速发展的的今天,当前的全球搜索引擎迅猛发展的市场环境下,搜索算法将在各大应用领域发挥它的巨大作用,可能下一个更加优的距离评估函数的发现,必将再次改变搜索算法的效率。
参考文献
[1]吕志刚,李琳,宇文超朋,郜辉.启发式搜索算法路径规划研究.西安.西安工业大学.2018
[2]刘云翔,杜杰,张晴.基于路径优化的A*算法与Dijkstra算法的性能比较.上海应用技术大学.2017
[3]张鸿.人工智能中求解八数码问题算法的实现与分析.郑州大学.2009
[4]周浩.八数码问题DFS和BFS算法的设计与实现.南京师范大学.2011
源码
import numpy as np
from math import sqrt
end = np.array([[1, 2, 3], [8, 0, 4], [7, 6, 5]]) # 最终节点
# 宽度优先搜索求解八数码问题
class BFS:
def __init__(self, arr, parent=None):
self.arr = arr
self.end = end
self.parent = parent
# 按顺序定义四个移动的方向
self.directions = ['left', 'up', 'right', 'down']
self.space = 0
# 打印路线
def showLine(self):
for i in range(3):
for j in range(3):
print(self.arr[i, j], end=' ')
print("\\n")
print('------>')
return
# 获取零所在的位置
def getZeroPos(self):
row, col = np.where(self.arr == self.space)
return row, col
# 扩展节点
def generateSubstates(self):
subStates = []
flag = 0 # flag用来判断该节点是否有后继节点
row, col = self.getZeroPos()
for direction in self.directions:
if 'left' == direction and col > 0:
# 判断零是否能向左移动
s = self.arr.copy()
s[row, col], s[row, col - 1] = s[row, col - 1], s[row, col]
if self.parent != None:
arr2 = s - self.parent.arr
if len(arr2[arr2 == 0]) < 9:
# 判断扩展出来的新节点是否与其父节点的父节点相同
# 若不相同则扩展,否则不扩展
news = BFS(s, parent=self)
subStates.append(news)
flag += 1
else:
news = BFS(s, parent=self)
subStates.append(news)
flag += 1
if 'up' == direction and row > 0:
# 判断零是否能向上移动
s = self.arr.copy()
s[row, col], s[row - 1, col] = s[row - 1, col], s[row, col]
if self.parent != None:
arr2 = s - self.parent.arr
if len(arr2[arr2 == 0]) < 9:
news = BFS(s, parent=self)
subStates.append(news)
flag += 1
else:
news = BFS(s, parent=self)
subStates.append(news)
flag += 1
if 'down' == direction and row < 2:
# 判断零是否能下左移动
s = self.arr.copy()
s[row, col], s[row + 1, col] = s[row + 1, col], s[row, col]
if self.parent != None:
arr2 = s - self.parent.arr
if len(arr2[arr2 == 0]) < 9:
news = BFS(s, parent=self)
subStates.append(news)
flag += 1
else:
news = BFS(s, parent=self)
subStates.append(news)
flag += 1
if 'right' == direction and col < 2:
# 判断零是否能向右移动
s = self.arr.copy()
s[row, col], s[row, col + 1] = s[row, col + 1], s[row, col]
if self.parent != None:
arr2 = s - self.parent.arr
if len(arr2[arr2 == 0]) < 9:
news = BFS(s, parent=self)
subStates.append(news)
flag += 1
else:
news = BFS(s, parent=self)
subStates.append(news)
flag += 1
return subStates, flag
# BFS搜索路径
def search(self):
opentable = [] # open表
closedtable = [] # closed表
opentable.append(self) # 将起始节点加入open表
generatednodes = 0 # 生成的节点个数
expendednodes = 0 # 扩展节点个数
while len(opentable): #判断open表是否为空
n = opentable.pop(0) #open表中的第一个节点
closedtable.append(n) #将open表中的第一个节点添加到closed表中
subStates, flag = n.generateSubstates() # 节点n扩展出来的子节点
generatednodes = generatednodes + len(subStates)
if flag:
expendednodes += 1
path = []
for s in subStates:
if (s.arr == s.end).all():
# 判断该子节点是否为目标节点
# 若是则返回路径
path.append(s)
while s.parent and s.parent != s0:
path.append(s.parent)
s = s.parent
path.reverse()
return path, generatednodes, expendednodes
opentable.extend(subStates)
return None, None, None
# 深度优先搜索求解八数码问题
class DFS:
def __init__(self, arr, depth, parent=None):
self.arr = arr
self.end = end
self.parent = parent
self.maxdepth = 15
self.directions = ['left', 'up', 'down', 'right']
self.space = 0
self.depth = depth
def getZeroPos(self):
row, col = np.where(self.arr == self.space)
return row, col
def showLine(self):
for i in range(3):
for j in range(3):
print(self.arr[i, j], end=' ')
print("\\n")
print('------>')
return
def generateSubstates(self):
subStates = []
flag = 0
row, col = self.getZeroPos()
for direction in self.directions:
if 'left' == direction and col > 0:
s = self.arr.copy()
s[row, col], s[row, col - 1] = s[row, col - 1], s[row, col]
if self.parent != None:
arr2 = s - self.parent.arr
if len(arr2[arr2 == 0]) < 9:
news = DFS(s, self.depth + 1, parent=self)
subStates.append(news)
flag += 1
else:
news = DFS(s, self.depth + 1, parent=self)
subStates.append(news)
flag += 1
if 'up' == direction and row > 0:
s = self.arr.copy()
s[row, col], s[row - 1, col] = s[row - 1, col], s[row, col]
if self.parent != None:
arr2 = s - self.parent.arr
if len(arr2[arr2 == 0]) < 9:
news = DFS(s, self.depth + 1, parent=self)
subStates.append(news)
flag += 1
else:
news = DFS(s, self.depth + 1, parent=self)
subStates.append(news)
flag += 1
if 'down' == direction and row < 2:
s = self.arr.copy()
s[row, col], s[row + 1, col] = s[row + 1, col], s[row, col]
if self.parent != None:
arr2 = s - self.parent.arr
if len(arr2[arr2 == 0]) < 9:
news = DFS(s, self.depth + 1, parent=self)
subStates.append(news)
flag += 1
else:
news = DFS(s, self.depth + 1, parent=self)
subStates.append(news)
flag += 1
if 'right' == direction and col < 2:
s = self.arr.copy()
s[row, col], s[row, col + 1] = s[row, col + 1], s[row, col]
if self.parent != None:
arr2 = s - self.parent.arr
if len(arr2[arr2 == 0]) < 9:
news = DFS(s, self.depth + 1, parent=self)
subStates.append(news)
flag += 1
else:
news = DFS(s, self.depth + 1, parent=self)
subStates.append(news)
flag += 1
return subStates, flag
#DFS搜索路径
def search(self):
opentable = [] # open表
closedtable = [] # closed表
opentable.append(self) # 将起始节点加入open表
generatednodes = 0 #生成的节点个数
expendednodes = 0 #扩展节点的个数
while len(opentable): #判断open表是否为空
n = opentable.pop(0) #open表中的第一个节点
closedtable.append(n) #将open表中的第一个节点添加到closed表中
subStates, flag = n.generateSubstates(以上是关于人工智能基于八数码问题对比搜索算法的性能的主要内容,如果未能解决你的问题,请参考以下文章