小航的算法日记组合数

Posted 2022-11-29

目录

• ​​一、概念​​
• ​​二、模板​​
• ​​三、例题​​

• ​​题：118. 杨辉三角​​
• ​​解：​​
• ​​题：119. 杨辉三角 II​​
• ​​解：​​

内容摘自英雄哥，以下是java版

一、概念

组合数递推公式：

---

eg.

等价于这两种情况之和：

边界处理：

当n=m=0、1，结果均为1种方案。

二、模板

杨辉三角

三、例题

题：118. 杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

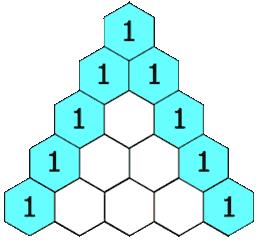
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

1 <= numRows <= 30

解：

解题思路：​​杨辉三角定义​​

AC代码：

class Solution 
    public List<List<Integer>> generate(int numRows) 
        List<List<Integer>> res = new ArrayList<>();
        for(int i = 0; i < numRows; i ++) 
            List<Integer> rows = new ArrayList<>();
            for(int j = 0; j <= i; j ++) 
                if(i == j || j == 0)
                    rows.add(1);
                else 
                    rows.add(res.get(i-1).get(j-1) + res.get(i-1).get(j));
                
            
            res.add(rows);
        
        return res;
    

题：119. 杨辉三角 II

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]

示例 2:

输入: rowIndex = 0
输出: [1]

示例 3:

输入: rowIndex = 1
输出: [1,1]

提示:

0 <= rowIndex <= 33

进阶：

你可以优化你的算法到 O(rowIndex) 空间复杂度吗？

解：

解题思路：​​滚动数组​​

AC代码：

class Solution 
    public List<Integer> getRow(int rowIndex) 
        List<Integer> pre = new ArrayList<>();     
        for(int i = 0; i <= rowIndex; i ++) 
            List<Integer> cur = new ArrayList<>();
            for(int j = 0; j <= i; j ++) 
                if(i == j || j == 0) cur.add(1);
                else cur.add(pre.get(j) + pre.get(j-1));
            
            pre = cur;
        
        return pre;
    

解题思路：​​线性递推​​

1. 杨辉三角每行数字对称，并且从1开始然后回到1
2. 根据组合数的递推公式可得：杨辉三角满足组合数的性质
3. 同一行的相邻组合数的关系：
   

AC代码：

class Solution 
    public List<Integer> getRow(int rowIndex) 
        List<Integer> res = new ArrayList<>();
        res.add(1);
        for(int i = 1; i < rowIndex + 1; i ++)  // 注意这里rowIndex从0开始数
            res.add((int)((long)res.get(i-1) * (rowIndex - i + 1) / i));
        
        return res;