高斯曲线的python绘制
Posted 道亦无名
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了高斯曲线的python绘制相关的知识,希望对你有一定的参考价值。
高斯曲线,又叫做gaussian curve,是正态分布中的一条标准曲线。卡尔·弗里德里奇·高斯(Carl Friedrich Gauss)在格丁根(Gottingen)的那座天文台是大约于1807年建成的。在他的整个一生中,从那时起:近200年的大部分时间里,天文仪器不断得到改进。我们今天所看到的一颗星辰的位置,在当时已被人们多次确定,因此,在我们看来,我们的观察似乎越来越趋于精确。但是,当我们将各次观察结果加以比较时,我们就会惊奇而懊丧地发现,它们仍然散乱无序。人们曾经希望观察的偏差终会消失,人们也会像上帝那样洞烛幽微的。但是,事实上,错误仍无法从观察中根除。无论是观察群星、原子、人的照片,还是听某人的讲演,都是这样。
GraphView中的高斯函数方程:
y=1/(0.4sqrt(2pi))e(-0.5((x-1)/0.4)2)
具体的实现效果代码如下:
# plot Gaussian Function
# 注:正态分布也叫高斯分布
import matplotlib.pyplot as plt
import numpy as np
import importlib
import sys
import matplotlib.font_manager as fm
importlib.reload(sys)
#sys.setdefaultencoding('utf8')
myfont= fm.FontProperties(fname='/usr/share/fonts/truetype/wqy/wqy-microhei.ttc')
u1 = 0 # 第一个高斯分布的均值
sigma1 = 1 # 第一个高斯分布的标准差
u2 = 1 # 第二个高斯分布的均值
sigma2 = 2 # 第二个高斯分布的标准差
x = np.arange(-10, 10, 0.1)
# 表示第一个高斯分布函数
y1 = np.multiply(np.power(np.sqrt(2 * np.pi) * sigma1, -1), np.exp(-np.power(x - u1, 2) / 2 * sigma1 ** 2))
# 表示第二个高斯分布函数
y2 = np.multiply(np.power(np.sqrt(2 * np.pi) * sigma2, -1), np.exp(-np.power(x - u2, 2) / 2 * sigma2 ** 2))
plt.subplot(121)
plt.plot(x, y1, 'b-', linewidth=2)
plt.title("高斯分布函数图像",fontproperties=myfont)
plt.subplot(122)
plt.plot(x, y2, 'r-', linewidth=2)
plt.title('高斯分布函数图像',fontproperties=myfont)
plt.show()
实现效果如下:
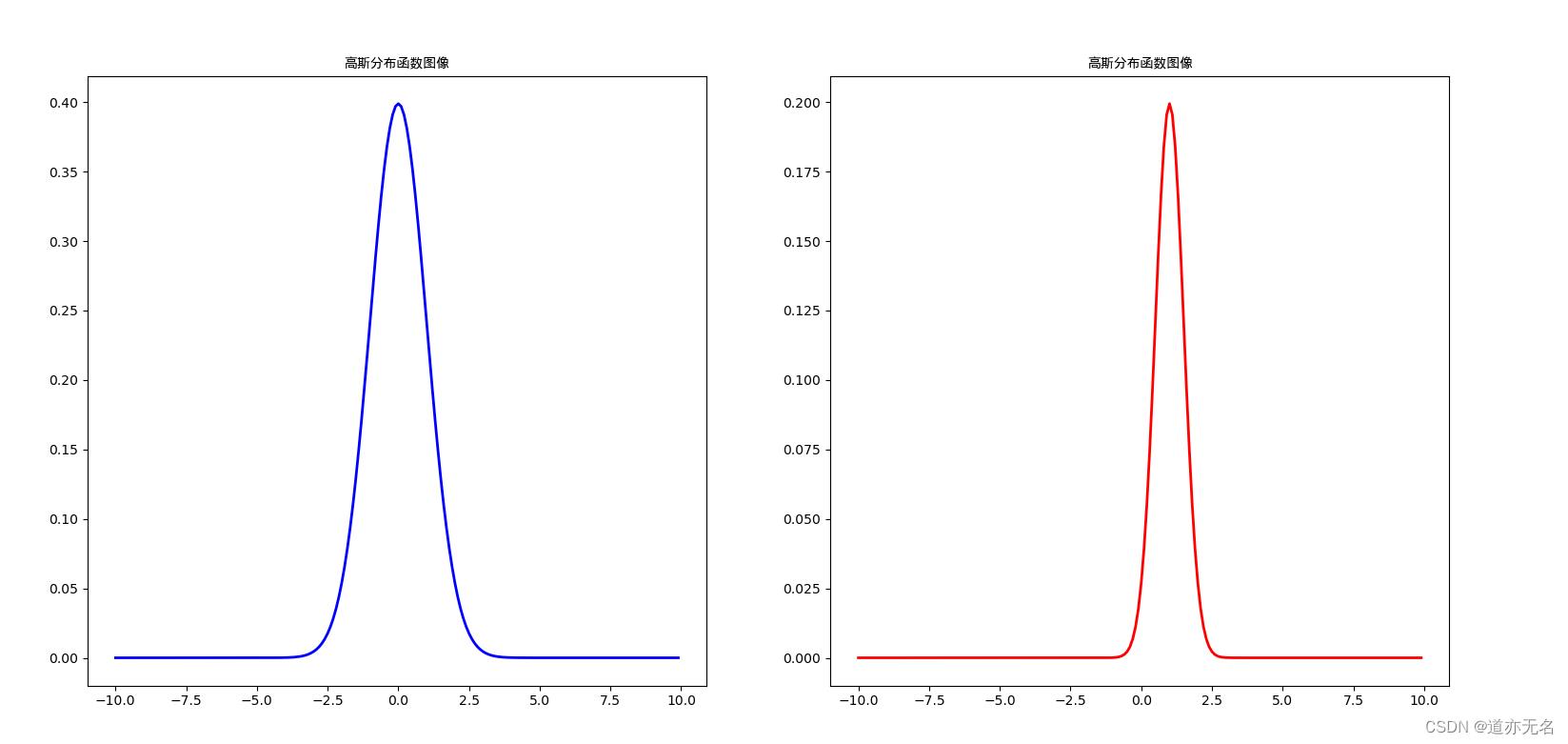
以上是关于高斯曲线的python绘制的主要内容,如果未能解决你的问题,请参考以下文章