使用python实现带回溯的梯度下降

Posted 2022-11-27 Babyface Killer

Gradient-based Method

在优化的领域里，gradient-based method表示每次迭代直接使用目标函数的gradient的相反方向作为下降的方向。于是每次迭代的更新方式可表示为：

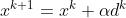 其中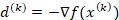  

Steepest Descent with Exact Line Search

Steepest descent是一种使用gradient-based method时可以最快收敛的方法。其算法原理是在每次迭代时为了确定最优的步长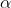，把目标函数转换为以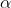为变量的函数并求其最优解，即在每次迭代时求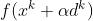最优解，这一步在优化领域统称为Exact Line Search可用于不同的迭代优化算法。因为每次迭代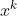与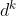都已确定，因此目标函数就可转化为一个只含一元变量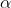的函数，由此可轻松求得最优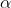值。且因为求得的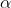可使得目标函数在当前取得最小值，于是该方法就因此被称为Steepest Descent Method。但在实际操作中，对于大量高维的数据每次迭代需要求得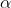的最优解依然是一个耗时耗力的过程。于是该方法就被简化为了下面的Backtracking method。

Backtracking Method

为了简便且有效的替代Exact Line Search，Backtracking算法以固定的速率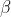减小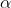直到目标函数满足预设的sufficient decrease condition。其算法如下：

对于每次迭代：

step 0: 使用预设的步长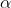

step 1: while sufficient decrease condition is not met：

                         =

step 2: 使用当前的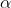计算下次迭代的值

其中的sufficient decrease condition通常使用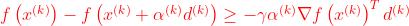：,其中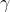为预设的参数

该方法虽然不能保证每次迭代都能得到当前最优的值，但可以保证每次迭代目标函数都能得到足够的下降，而这一点就是由sufficient decrease condition来控制的。

使用python实现Backtracking Gradient-descent

下面展示使用python实现Backtracking gradient-descent的代码，因在实际计算过程中由于舍入误差算法不能保证收敛到最优解，代码中设置了停止条件为迭代次数达到1000次或当前gradient足够小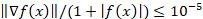：（gradient =0 时为算法达到最优解）。为了便于观察结果，若到达最优解前迭代次数小于15次则输出每次迭代结果，若大于15次则仅输出前十次迭代结果和最后五次迭代结果。

def backtracking(function,gradient,initial_s,gamma,beta,initial_x):
    """
    Description: 
    Gradient-based method with backtracking to
    find the minimum of a multivariant function
    Parameters:
    function: objective function to be minimized
    gradient: gradient of objective function
    initial_s: initial guess of step length
    gamma: real number between 0 and 1 to 
    test if the function is decreased sufficiently
    beta: real number between 0 and 1 to decrease the 
    step length if the original one does not make
    sufficient decrease
    initial_x: initial point
    """
    # import library
    import numpy as np
    # set maximum number of iteration
    max_iter=1000
    # set stop criteria
    stop_criteria=1E-5
    # print initial point
    print('Initial point: .T'.format(initial_x.reshape(1,-1)))
    # set x to initial point
    x_k=initial_x
    # set s to initial s
    s=initial_s
    # create lists to store result
    d_k_list=[]
    s_list=[]
    x_k_list=[]
    # iterate until maximum iteration is reached 
    for iter in range(max_iter):
        # calcualte gradient value
        gradient_k=gradient(x_k)
        # calcualte function value
        function_k=function(x_k)
        # set s to initial s
        s=initial_s
        # check stop criteria
        if ((np.linalg.norm(gradient_k)/(1+np.abs(function_k))) > stop_criteria):
            # descent direction
            d_k=-gradient_k
            # next point
            x_k_plus_one=x_k+s*d_k
            # check if the sufficient decrease condition is met
            while (function(x_k) - function(x_k-s*gradient(x_k))) < (-gamma*s*np.dot(gradient_k.T,d_k)):
                # update step length
                s=beta*s
                # re-calculate next point
                x_k_plus_one=x_k+s*d_k
            # update x
            x_k=x_k_plus_one
            # put result in lists
            d_k_list.append(d_k)
            s_list.append(s)
            x_k_list.append(x_k)
        # if the stop criteria is satisfied
        else:
            # print out the solution
            print('Solution found: .T'.format(x_k.reshape(1,-1)))
            # break the iteration
            break
    # print result
    # if iteration less than 15 print each iteration
    if iter < 15:
        for i in range(iter):
            print('=====Iteration====='.format(i+1))
            # print search direction
            print('Search direction: .T'.format(d_k_list[i].reshape(1,-1)))
            # print step length
            print('Step length: '.format(s_list[i]))
            # print new iterate
            print('New iterate: .T'.format(x_k_list[i].reshape(1,-1)))
    # if iteration is greater than 15
    else:
        # print first 10 iterations
        for i in range(10):
            print('=====Iteration====='.format(i+1))
            # print search direction
            print('Search direction: .T'.format(d_k_list[i].reshape(1,-1)))
            # print step length
            print('Step length: '.format(s_list[i]))
            # print new iterate
            print('New iterate: .T'.format(x_k_list[i].reshape(1,-1)))
        print('''
        ..........
        ..........''')
        # print last 5 iterations
        for i in range(5):
            print('=====Iteration====='.format(iter-3+i))
            # print search direction
            print('Search direction: .T'.format(d_k_list[iter-5+i].reshape(1,-1)))
            # print step length
            print('Step length: '.format(s_list[iter-5+i]))
            # print new iterate
            print('New iterate: .T'.format(x_k_list[iter-5+i].reshape(1,-1)))
        # print warning if maximum iteration is reached
        if iter == 999:
            print('====================')
            print('Maximum iteration is reached !!!')

    测试算法

使用一个非线性函数来测试用Python实现的Backtracking算法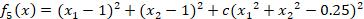：，其中c值分别使用1，10，100来观察算法收敛速度。为了方便比较起始点都设为[1,-1]，初始步长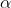为1，步长下降速率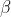为0.5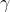，设为0.3.

当c=1时：

Solution found: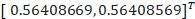

Iterations used: 10

当c=10时：

Solution found: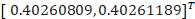

Iterations used: 19

当c=100时：

Solution found: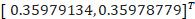

Iterations used: 210

对于Gradient-based method来说，若目标函数为二次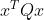：，则收敛速度取决于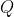的最大特征值和最小特征值的比值，若比值越大则收敛速度越慢；若目标函数为高次函数，则取决于目标函数在最优解（stationary point）的Hessian matrix的最大特征值和最小特征值的比值。 

该测试函数为高次函数，当c=1，c=10及c=100时其Hessian matrix在最优解点的Hessian matrix分别为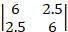：（最大特征值/最小特征值=2.4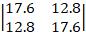），（最大特征值/最小特征值=6.1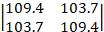，（最大特征值/最小特征值=37.4）。由此结果可验证，以上使用python实现的算法符合Gradient-based method的收敛理论。