论文阅读自然语言模型的尺度法则（CS224N WINTER 2022 Lecture17 推荐阅读整理）

Posted 2022-11-26 囚生CY

• 英文标题：Scaling Laws for Neural Language Models
• 中文标题：自然语言模型的尺度法则
• 下载链接：arxiv@2001.08361

---

序言

本文是CS224N WINTER 2022 （六）前沿问题探讨（QA、NLG、知识集成与检索、Coreference）的lecture 17内容的补充（只有一篇推荐阅读，就是这一篇）。

本文属于经验性实验分析论文，大部分结论缺少理论推导，不过神经网络这块本身就很少涉及理论推导，笔者觉得很多结论还是很受用的。

---

文章目录

• 序言
• • 摘要 Abstract
  • 1 导论 Introduction
  • • 1.1 概述 Summary
    • 1.2 尺度法则概述 Summary of Scaling Laws
    • 1.3 数学标记 Notation
  • 2 研究背景与研究方法 Background and Methods
  • • 2.1 Transformer的参数与计算尺度 Parameter and Compute Scaling of Transformers
    • 2.2 训练步骤 Training Procedures
    • 2.3 数据集 Datasets
  • 3 经验结果与基本乘幂法则 Empirical Results and Basic Power Laws
  • • 3.1 Transformer近似形态与超参数独立性 Approximate Transformer Shape and Hyperparameter Independence
    • 3.2 无嵌入参数量$N$的性能 Performance with Non-Embedding Parameter Count $N$
    • • 3.2.1 LSTM和通用Transformer的比较 Comparing to LSTMs and Universal Transformers
      • 3.2.2 推广到不同数据分布 Generalization Among Data Distributions
    • 3.3 数据量与计算力对性能的影响 Performance with Dataset Size and Compute
  • 4 无穷数据限制与过拟合绘图 Charting the Infinite Data Limit and Overfitting
  • • 4.1 提出的$L(N,D)$方程 Proposed $L(N,D)$ Equation
    • 4.2 实验结果 Results
  • 5 模型尺寸与训练时间的尺度法则 Scaling Laws with Model Size and Train Time
  • • 5.1 $B_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}(L)$处的训练调整 Adjustment for Training at $B_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}(L)$
    • 5.2 $L(N,S_{\min })$的结果以及模型尺寸和计算量对性能的影响 Results for $L(N,S_{\min })$ and Performance with Model Size and Compute
    • 5.3 提前停止步骤的下界 Lower Bound on Early Stopping Step
  • 6 计算量预算的最优分配 Optimal Allocation of the Computer Budget
  • • 6.1 最优性能与分配 Optimal Performance and Allocations
    • 6.2 从$L(N,S_{\min })$得到的预测结果 Predictions from $L(N,S_{\min })$
    • 6.3 矛盾与一个猜想 Contradictions and a Conjecture
  • 7 相关工作 Related Work
  • 8 讨论 Discussion
  • 附录 Appendices
  • • A 尺度法则总结 Summary of Power Laws
    • B 计算有效边界的经验模型 Empirical Model of Compute-Efficient Frontier
    • • B.1 定义方程 Defining Equations
      • B.2 高效训练 Efficient Training
      • B.3 与低效情形的对比 Comparison to Inefficient
      • B.4 次优的模型尺寸 Suboptimal Model Sizes
    • C 警告 Caveats
    • D 附图 Supplemental Figures
    • • D.1 早停与测试训练对比 Early Stopping and Test vs Train
      • D.2 通用Transformer架构 Universal Transformers
      • D.3 批训练量 Batch Size
      • D.4 样本效率与模型尺寸 Sample Efficiency vs Model Size
      • D.5 上下文独立性 Context Dependence
      • D.6 学习率规划与误差分析 Learning Rate Schedules and Error Analysis
      • D.7 拟合细节与乘幂法则质量 Fit Details and Power Law Quality
      • D.8 推广与架构 Generalization and Architecture
  • 参考文献 References

---

摘要 Abstract

• 本文研究的是基于交叉熵损失的语言模型性能的经验尺度法则（empirical scaling laws）。

• 本文使用乘幂法则（power laws）来刻画模型训练的交叉熵与模型尺寸（model size，即模型参数量）、数据集量、训练计算量的关系。一些其他的模型架构细节（如网络宽度或深度）对交叉熵损失的影响很小。

• 本文利用简单的方程来刻画过拟合程度对模型尺寸或数据集量的依赖性，以及模型训练速度对模型尺寸的依赖性，这些关系可用于计算资源的合理分配。

• 本文发现大模型使用样本的效率显著更高，因此最优的高效训练方式是在中等（modest）数据集上训练超大模型（very large models），并在显著收敛前提前停止（stop significantly before convergence）。

---

1 导论 Introduction

语言模型的性能可能取决于模型架构、模型尺寸、训练计算量、训练数据量，本文将对这些因素在Transformer模型架构上进行逐一分析。

---

1.1 概述 Summary

本文在Transformer语言模型上实验的关键成果概述：

1. 模型性能与尺度（scale）强相关，与模型形态（model shape，即网络层的宽度和深度等）弱相关：Section 3

   尺度由三部分组成（模型参数量$N$，训练数据量$D$，训练计算量$C$），在合理范围内，模型性能与网络层的宽度或深度关联性很低。

2. 平滑乘幂法则（smooth power laws）：Section 3

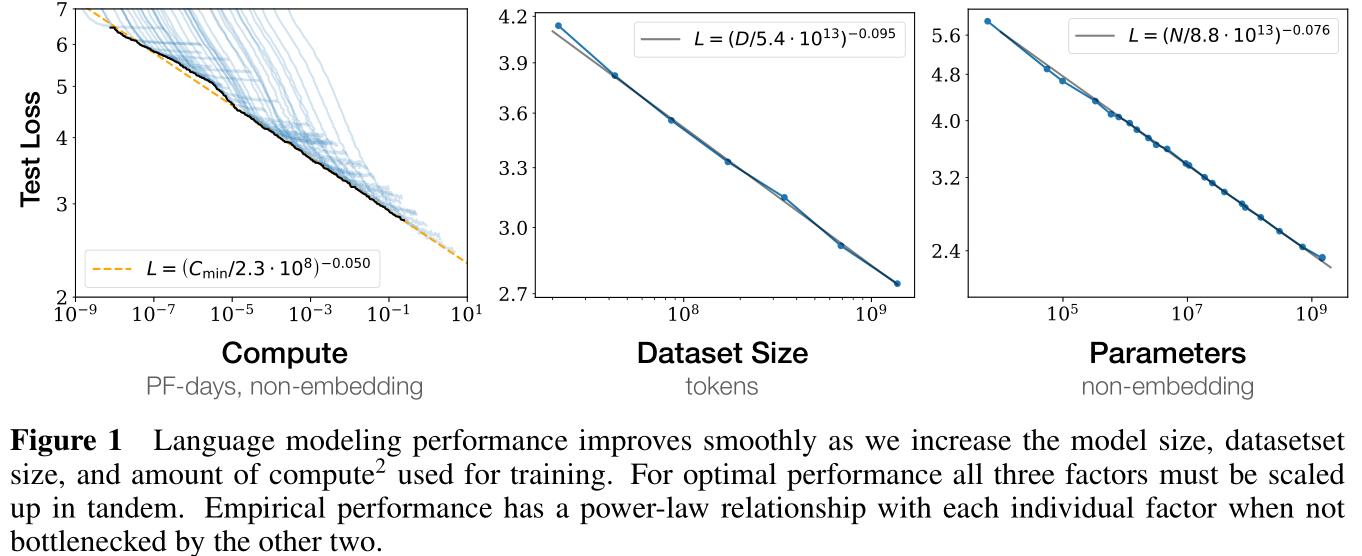
   在固定其中一个尺度因素（scale factor），其余两个尺度因素不加限制的条件下，模型性能与三个尺度因素（$N,D,C$）具有乘幂法则关系（Figure 1）。

   Figure 1：

   • 横轴表示三个尺度因素，纵轴表示对测试集上的损失值（用于衡量模型性能）；
   • 途中可以看出三个尺度因素对模型性能的近似是对数平滑的，具体拟合方程已在图中标注；

   

3. 过拟合的普遍性（Universality of overfitting）：Section 4

   只要同时扩大$N,D$，模型性能（指损失值）自然会提升，但是如果固定$N,D$中的某一个的数值，然后扩大另一个的数值，模型性能反而会衰减（即发生过拟合）。具体而言，性能衰减程度与$N^{0.74}/D$的比率相关，即如果扩大模型尺寸八倍，就需要将训练数据来扩大五倍。

4. 模型训练的一般性（Universality of training）：Section 5

   训练曲线（training curves，即损失值曲线）是可以通过乘幂法则进行预测，且近似可以认为与模型尺寸独立（即只考察与$N,D$的关系），通过训练曲线早期走势可以推断得到最终训练损失值能够收敛到何处。

5. 迁移提升测试性能（Transfer improves with test performance）：Secition 3.2.2

   当我们将模型在与训练数据分布不同的测试数据上进行评估时，结果表明尽管存在一定的模型性能损失，但是整体上来看如果验证集上能够得到更好的模型性能，测试集上的模型性能也会有所提升。

6. 样本高效性（sample efficient）：

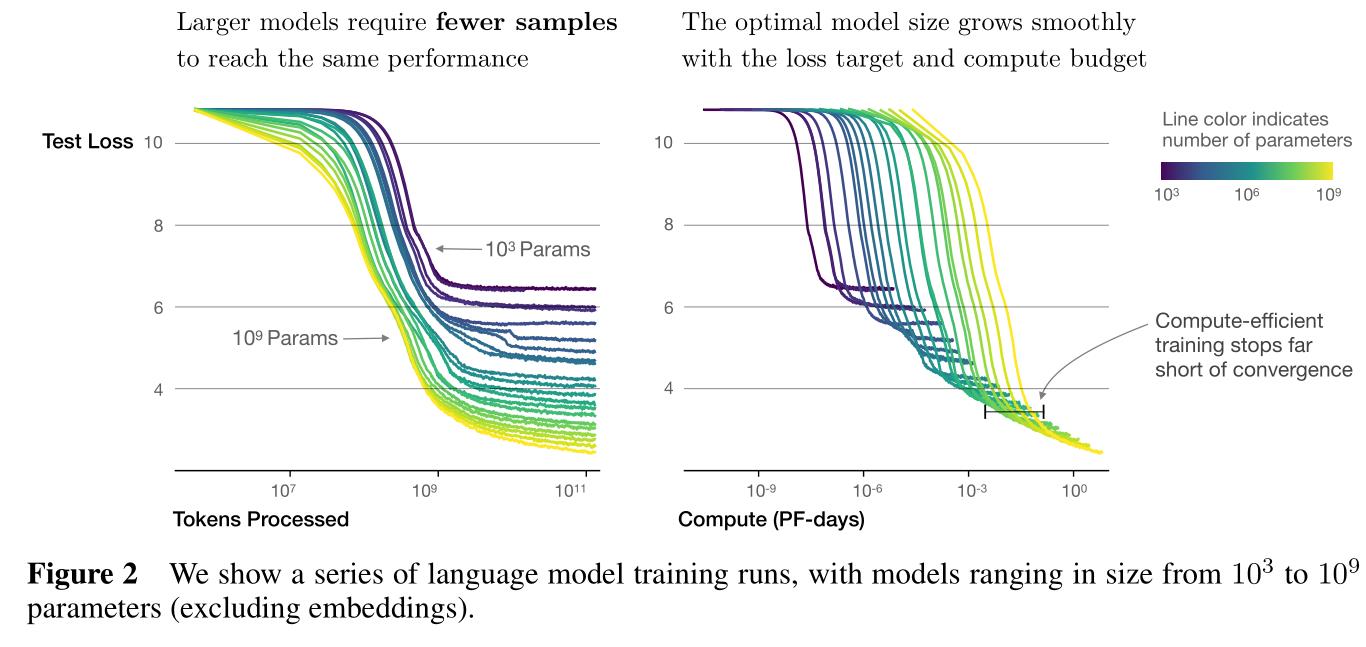
   大模型比小模型对样本信息的利用更高效，具体而言在更少的优化迭代次数时即可达到同等的模型性能（Figure 2）且需要更少的训练数据（Figure 4）。

   Figure 2：

   • 纵轴表示模型性能（即测试损失值，越低越好），左图横轴表示训练数据量，右图横轴表示训练时间；
   • 图中曲线颜色越深表明模型尺寸（即模型参数量）越少，说明要达到同样的测试损失值需要花费更多的训练数据（左图），右图其实说明的是大模型尽管耗时更长，但是模型性能的上限更高；

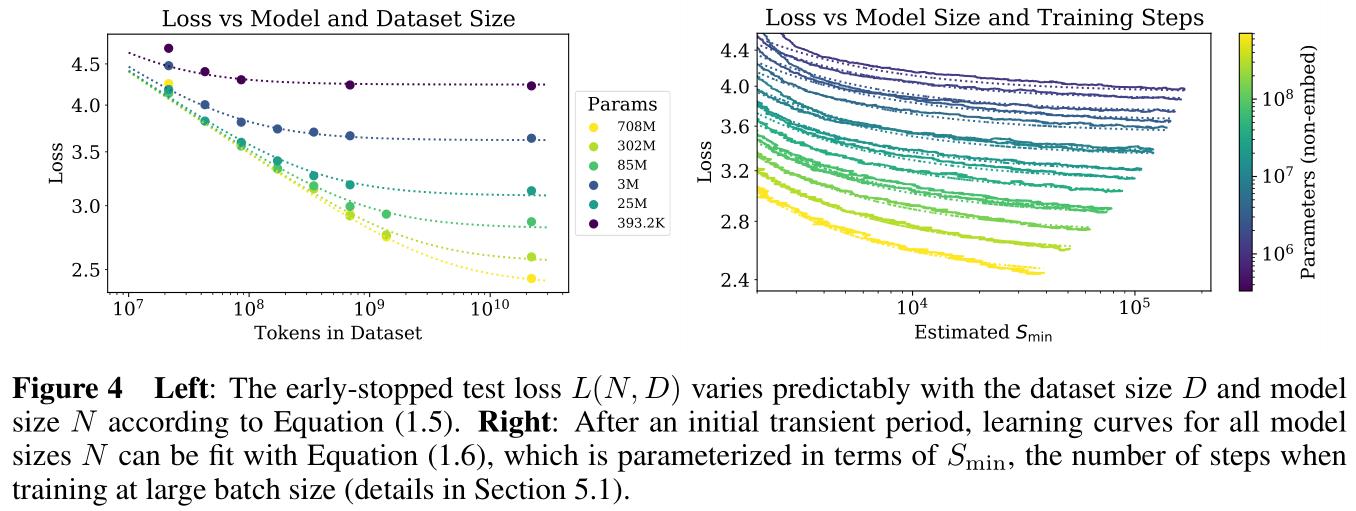
   Figure 4：

   • 纵轴表示模型性能（即测试损失值，越低越好），左图横轴表示训练数据量，右图横轴表示训练时间；
   • 图中曲线颜色越深表明模型尺寸（即模型参数量）越小，两图表明模型尺寸越大、训练数据量越大、训练时间越长，模型评估越好（符合直觉）；

   

   

   ---

7. 收敛是低效的（convergence is inefficient）：Section 6

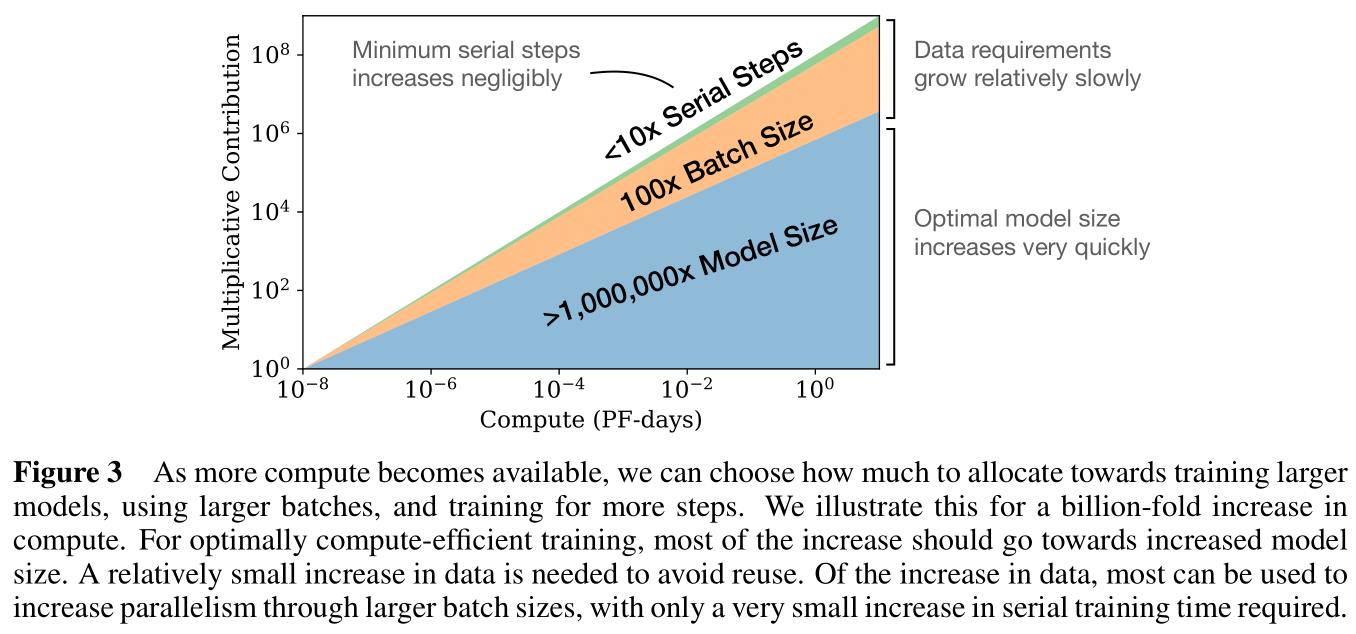
   在固定算力预算（compute budget）$C$，且不限制模型尺寸$N$和训练数据量$D$的假定下，获得最优模型性能的训练方式是训练超大模型并在显著收敛前停止（Figure 3），这种方式要比训练小模型直至收敛要样本高效得多。此外，实验表明$D\sim C^{0.27}$，即随着算力提升，需要的训练数据并没有增长太多。

   Figure 3：

   • 横轴表示算力，纵轴表示对模型性能的贡献提升，整体是一个累积面积图；
   • 随着算力提升，可以考虑训练更大的模型，或使用更大的批训练量，或训练迭代更多的轮次，实验表明应当将更多的算力应用到训练大模型上；

   

   ---

8. 最优批训练量（optimal batch size）：Section 5.1

   根据参考文献MKAT18，理想的批训练量近似为损失函数值的幂（power of the loss），并且随着梯度噪声尺度（gradient noise scale）不断调整。本文实验中使用的最大模型，每次可以批训练十亿到二十亿量级的分词。

---

1.2 尺度法则概述 Summary of Scaling Laws

用于构建自回归语言模型的Transformer测试损失值可以通过乘幂法则进行预测（利用Figure 1中关于$N,D,C$的拟合方程）：

1. 测试损失值与非嵌入参数量的关系：限制模型参数量，在充分大的训练集上训练至损失值收敛

   $$L(N)={\left(\frac{N_c}{N}\right)}^{{\alpha }_N};{\alpha }_N\sim 0.076;N_c\sim 8.8\times 10^{13}\text{(non-embedding parameters)}\text{\hspace{1em}(1.1)}$$

2. 测试损失值与训练数据量的关系：限制训练数据量，在大模型上训练至早停（early stopping）

   $$L(D)={\left(\frac{D_c}{D}\right)}^{{\alpha }_D};{\alpha }_D\sim 0.095;D_c\sim 5.4\times 10^{13}(\text{tokens})\text{\hspace{1em}(1.2)}$$

3. 测试损失值与训练时间的关系：限制训练计算量，在充分大的训练集上训练最优尺寸的模型（以充分小的批训练量）

   $$L(C_{\min })=(\frac{C^{以上是关于论文阅读自然语言模型的尺度法则（CS224N\; WINTER\; 2022\; Lecture17\; 推荐阅读整理）的主要内容，如果未能解决你的问题，请参考以下文章}}{C_{\min }}$$

   论文阅读自然语言模型的尺度法则（CS224N WINTER 2022 Lecture17 推荐阅读整理）

   CS224n笔记8 RNN和语言模型

   CS224N WINTER 2022RNN语言模型梯度消失与梯度爆炸（附Assignment3答案）

   CS224N WINTER 2022RNN语言模型梯度消失与梯度爆炸（附Assignment3答案）

   CS224N WINTER 2022RNN语言模型梯度消失与梯度爆炸（附Assignment3答案）

   CS224N WINTER 2022机器翻译注意力机制subword模型（附Assignment4答案）