规划问题求解的理论---线性代数

Posted 2022-11-25 willwillie

概述

谈到规划问题的时候，我们不得不谈到线性代数的内容。大学的时候，同学们应该都上过一门课—《线性代数》，这门课当时让人非常的反感，因为全是证明和定理，学起来毫无趣味。

“没有比线性代数更加基础的了，虽然事实上一代又一代的教授和图书编写者们通过荒谬的矩阵计算将线性代数的简单特性变得非常的模糊”。
但是如果说能从一个新的有趣的角度让你对这些知识重新装在脑袋里，而且还不会忘记，你会不会乐意接受？
通过线性代数你可以轻松理解原来的那些概念 基 线性空间 秩 ，最重要的是，通过这些知识，你可以很快的解决很多现实问题，你愿不愿意去学习？

是的 我们还是不清楚是否要去学习这样一门枯燥无味的学科。

我看过的最好的视频是 Essence of linear algebra，也推荐你看， 或许这里可以给出较好的解答，另外下面一个章节我将尽我所能给出我的解答。

形象的理解线性代数

1.什么是vector?

上图：向量可以代表现实的不同维度一些量

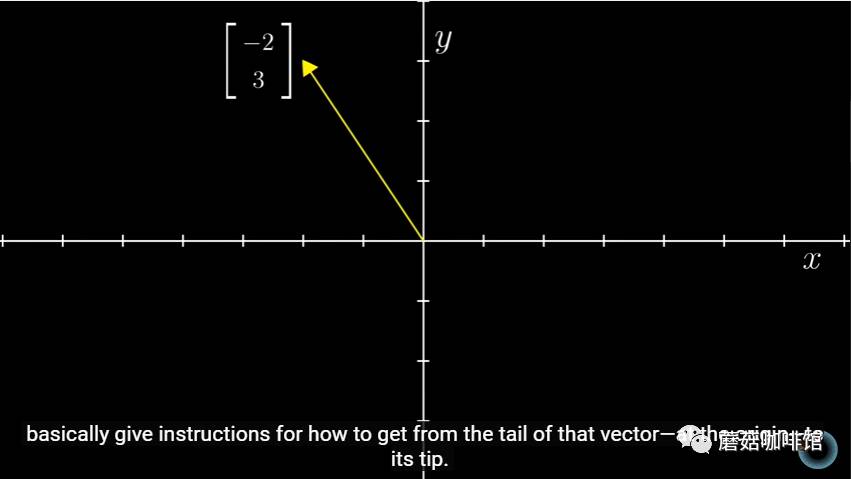
上图是在空间建模后，以原点为起点的二维向量

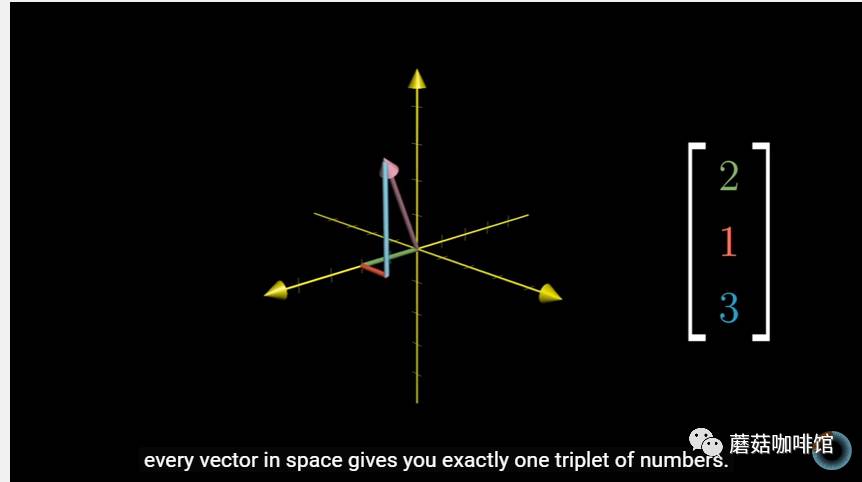
上图是三维空间中的一个向量；


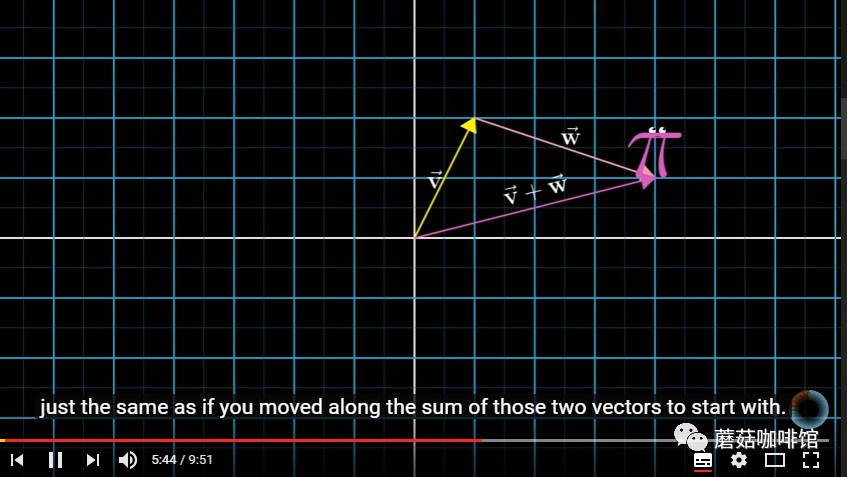
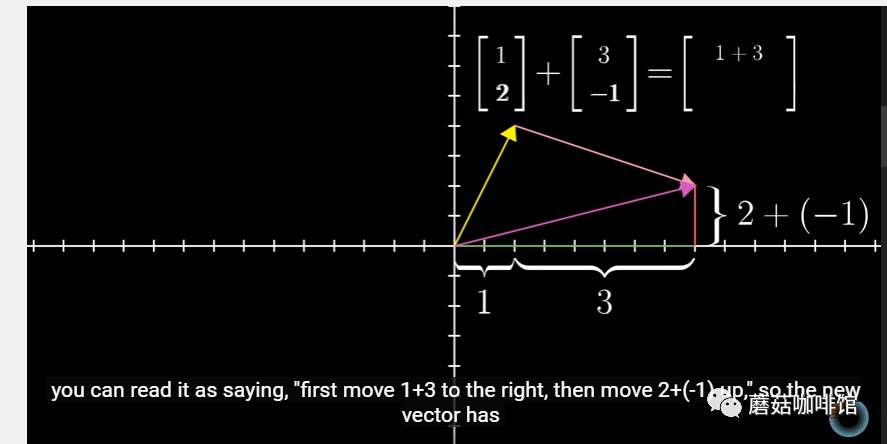
上面的两个图表示向量的加法的几何vision展现

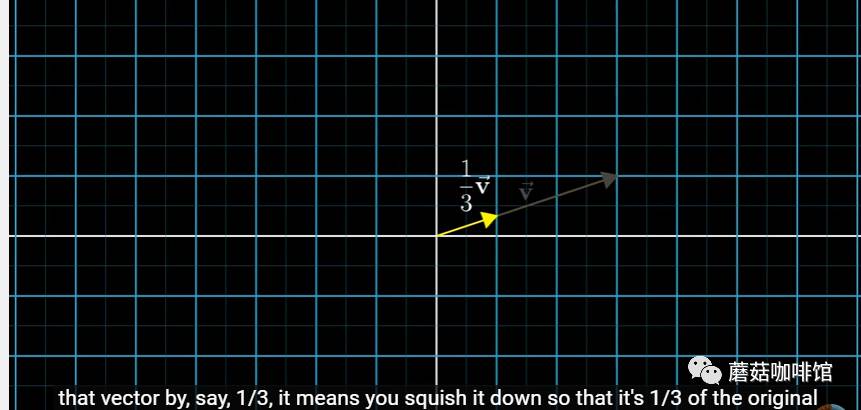
上面的图表示向量乘以一个数

span:如果将一个空间中的任一向量做任一方向的变化，那么这个向量的转换将会充满这整个空间。

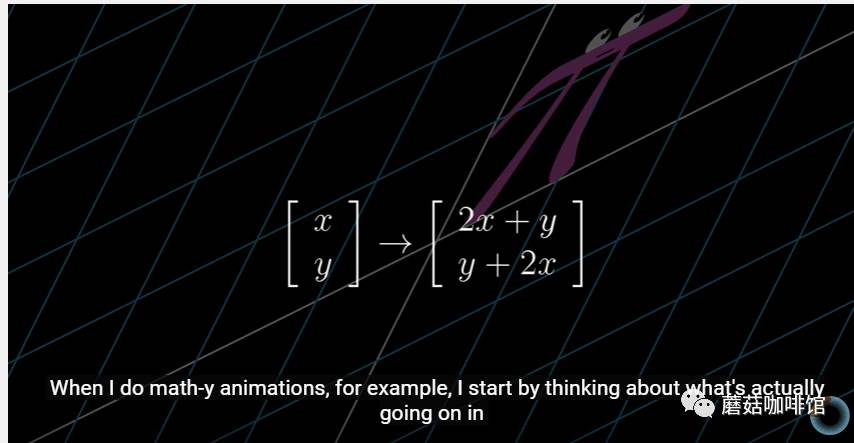
通过一个n维向量的乘法可以将一个向量做转换？

2.什么是线性转换？
需要满足两个条件的转换就还是线性转换：那就是lines remains lines以及原点保持不变。

上图所示的就是线性变换了；

一个向量或者说一个点经过线性转换之后变成了什么样子？
比如说在二维空间中：先选定一组基向量

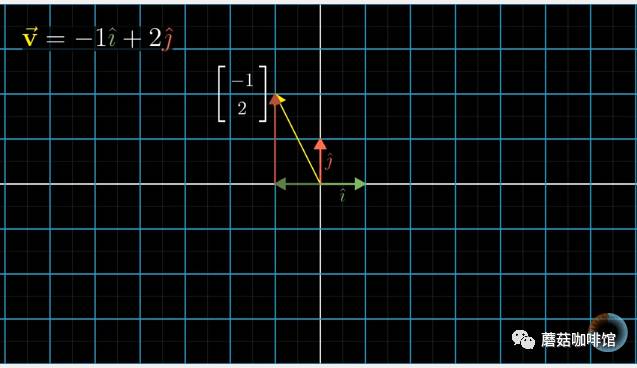
选定了基向量之后，空间中的任意向量都可以用这组i,j来表示了。
经过观察发现，经过变换之后，还是可以用这组变换后的基向量来表示，而且表示的关系不变。


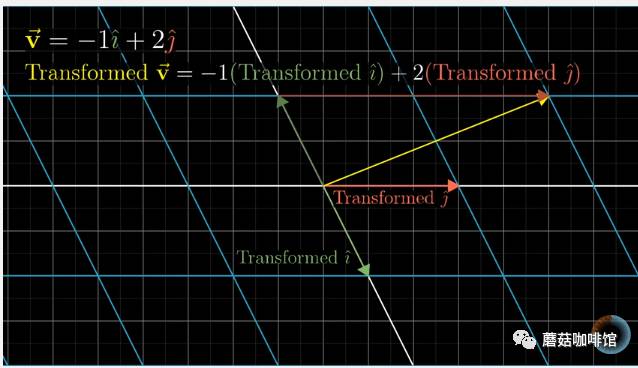
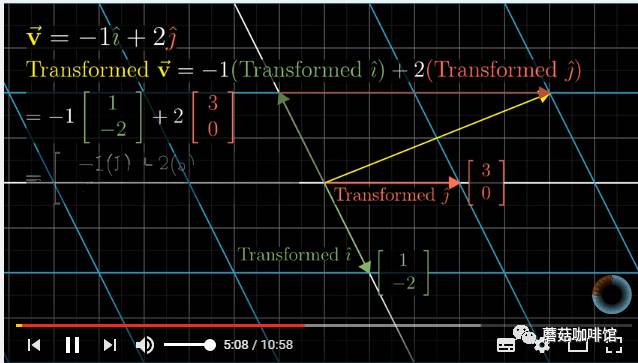
这样的话，矩阵乘以向量在几何意义上其实就是空间的转换了，

比如说将平面90°旋转：

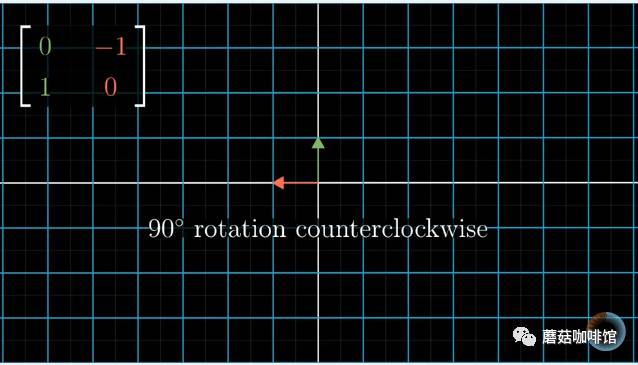
就是对平面上的任一向量乘这样一个矩阵。

从这一节视频理解基本上帮了很大的忙了

线性规划的建模就是这样的了

求解线性规划问题

深刻学完线性代数的相关内容，下面就可以开始讲到线性规划用到的解法单纯形法，理解起来也就不会那么痛苦了。

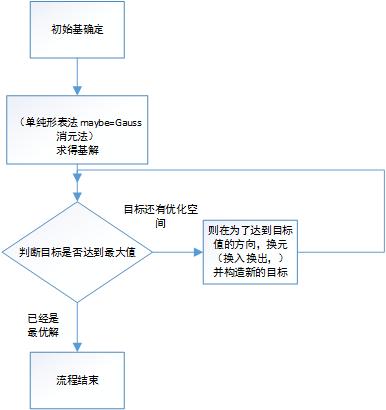
对于这个图，只要有人教我们说这个单纯形法就是这样子来的，你只要按照这个步骤来做，就可以解决线性规划的问题。但是我总是有一个，有时候又说不出来自己的疑问究竟是什么？其实我的疑问就是我理解上的那一层迷雾，为什么用单纯形法就可以解答出线性规划的问题，另外，单纯形法的每一个步骤又代表了什么意义？

还好，在我的另外一个blog线性规划和约束满足问题的思考中我已经给出了比较详细的解答，

单纯形法的做法是通过给不等式添加松弛变量将线性规划问题化为标准形式，选定一组基，令非基变量全为0，则求出一组基变量的解，这样得到的解当然不一定是最优的，可以将目标函数表示为非基变量的表达式，然后判别目标函数是否达到了最优（变量前面的参数<=0），如果不是，就想办法让目标能够更优。想什么办法呢?既然基变量不是唯一的，如果变量的参数大于0，就选择那个最大的参数的变量作为换入变量（至少换入变量的值>=0）,再从原来的基变量中选择一个作为换出变量（这个时候要使得换入变量的值最大，此时基变量都可以酸的一个值（将值最小的基变量换出应该可以？）），这样就会求得一组解，然后得到又一个目标表达式（此时目标表达式的值必然已经增大了，但是表示的方法变了（再一次判断是否达到了最大值）），直到最大为止。
其实通过给不等式添加松弛变量将线性规划问题转化为更加高维的空间问题，选定基变量的过程，将高维空间映射到更加低维的空间，这样可以求得一个目标值，然后判断目标值是否有增长的空间，如果有，就换一组基变量，将问题的高维空间映射到另外一个低维空间，然后再次判断目标值是否达到了最大，没有的话，继续将高维空间转化成新的低维空间，直到目标值达到最大为止。

其实这里映射的思想是理解单纯形法的关键，映射的概念算是来自线性代数了，仔细体会吧~~

除了单纯形法，还有对偶单纯形法；对偶单纯形法是建模的过程中将问题完全建立成对偶的模式，于是和原问题对比，他们的解也是对偶的；这样就能够完全有对偶的最优解。只要判断得到的解是否相等，你就能够证明你得到的解就是最优解了。

参考文档

1.https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
2.《运筹学.第三版》，清华大学出版社