弗洛伊德算法介绍 弗洛伊德算法资料

Posted 2023-05-03

参考技术A 1、Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

2、在计算机科学中，Floyd-Warshall算法是一种在具有正或负边缘权重（但没有负周期）的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度（加权）。虽然它不返回路径本身的细节，但是可以通过对算法的简单修改来重建路径。该算法的版本也可用于查找关系R的传递闭包，或（与Schulze投票系统相关）在加权图中所有顶点对之间的最宽路径。

图论应用 floyd（弗洛伊德）算法dijkstra（迪杰斯特拉）算法

前言

图论应用是非常广泛的，不同于二叉树，二叉树是应用在数据存储结构提高查询效率的，而图论则是用在辅助决策系统中，求得最优化解的等等，而本篇文章中介绍的floyd（弗洛伊德）算法、dijkstra（迪杰斯特拉）算法 是分别用于解决多元路径和最短路径问题的。应用比较广泛。辅助决策系统中使用

弗洛伊德算法

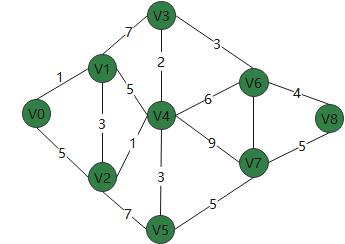
这个算法是为了解决多元路径问题的出现，从而找到最优的路径。 例如 下面的例子

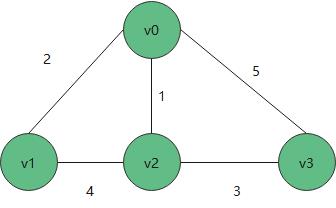
 从v1到v3之间的路径上有多种方式，但是权重是不相同的，两个节点之间得最短路径，用下图 邻接矩阵去表示

 弗洛伊德算法不管是有向图还是无向图，都能统计出一个节点到另一个节点最短路径，他可以找出整个图中节点之间得最短路径，所以叫多源最短路径算法。在算法实现中，通过邻接矩阵去实现。

算法分析

• 从v0开始，找每个节点得最短路径，把v0给锁住

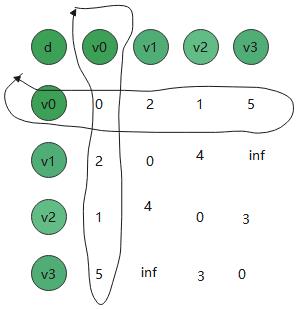
 第一行 就是 v0到v1 和 v0到v2 v0到v3 然后倒过来得距离， 这个初始值，有个点是在v0到v3，如果经过v2权重路径是比v0直接到v3路径短得。 也就是 5和4（3+1）得权重

所以 我们从v1开始 到v2 的最短路径，中转点了 我们从左开始不断进行看点修正

从v1走到v2路径

v1->v2 4

v1->v0->v2 2+1=3

明显经过中间点，就最近了

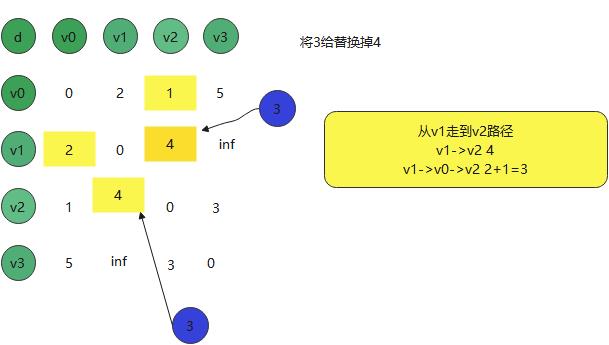
 已经就把以0为跳板将某个点进行修正了最短路径了。v1到v2 以0为中介转折点

 看v1到v3 从直观来看就是经过了两个节点，路径最小，因此有可能出现多个中转节点的情况

都经过算一次

 

 

 

 

这样得出最短路径 ，也就是不断修正数据，经过分析，从一个节点到另一个节点的最短路径

这样就能找到最短的路径了。

另外需要一个路径数据记录好修改的路径，这个需要记录上面的 更改的过程  路径更改的过程，当然这个路径可以任意取值的，我们注意的关键点在于值得修改

 

 

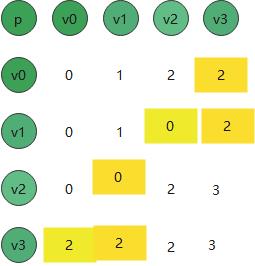
         这样我们就能记录好其中得跳板节点。

代码实现

首先我们先建两个邻接矩阵

  public static final int I = 100;
    //邻接距阵
    public static int[][] d = new int[][]{
            {0, 2, 1, 5},
            {2, 0, 4, I},
            {1, 4, 0, 3},
            {5, I, 3, 0}
    };
    public static int[][] p=new int[][]{
            {0,1,2,3},
            {0,1,2,3},
            {0,1,2,3},
            {0,1,2,3}
    };

而向矩阵中填数据，则预先填了，生成这个很简单就不用通过代码生成

然后弗洛伊德算法 方法

    public static void floyd(){
        for (int k = 0; k < d.length; k++) {
            for(int i=0;i<d.length;i++){
                for (int j = 0; j < d.length; j++) {
                    if(d[i][j]>d[i][k]+d[k][j]){
                        d[i][j]=d[i][k]+d[k][j];
                        //记录下路径
                        p[i][j]=p[i][k];
                    }
                }
            }
        }
    }

两层循环可以将二维数组都遍历得到， 遍历同时 d[i][j]>d[i][k]+d[k][j] 不断判断，也就是记录更小的数据，进行赋值，并将记录好变化的节点。

时间复杂度是n的三次方。经过三层循环就能找到对应的值，就是通过三层循环去找到对应的值。

迪杰斯特拉算法

上面的弗洛伊德算法算法去求任意两个顶点之间的最优路径问题，性能是比较低的，n的三次方法，但是不能改变的。 

而迪杰斯特拉算法，相当于弗洛伊德算法算法的提升，只需要求某个顶点到其他任意顶点的最短路径，起点只能从一个点开始

 

 

 

核心思想

我们用一个v0点为开始点，我们去查找到任意个点的最短路径。

• 首先建立两个集合，假设为U  和V   从那个节点开始，我们就先将节点放到U集合中

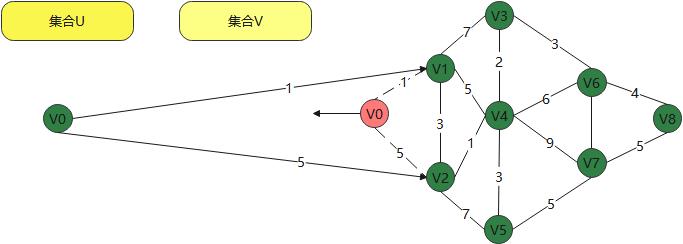
 以当前节点开始找到最短路径 如果小的路径，继续拿过来

 现在从v0到v2的路径有  经过v1和直到的两种方式，然后新建权重数组和路径数组，

权重数组保存经过的权重，而路径数组用来保存前面的顶点 

 这样不断的往前走，当到v3时，不可达，就直接跳过v3,到v4

 

 

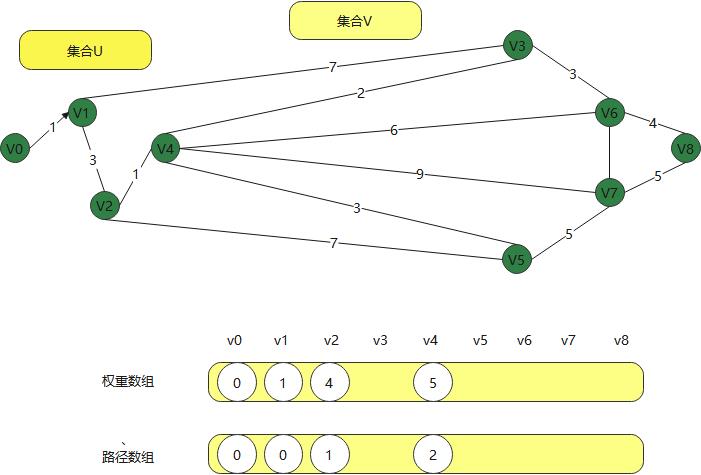
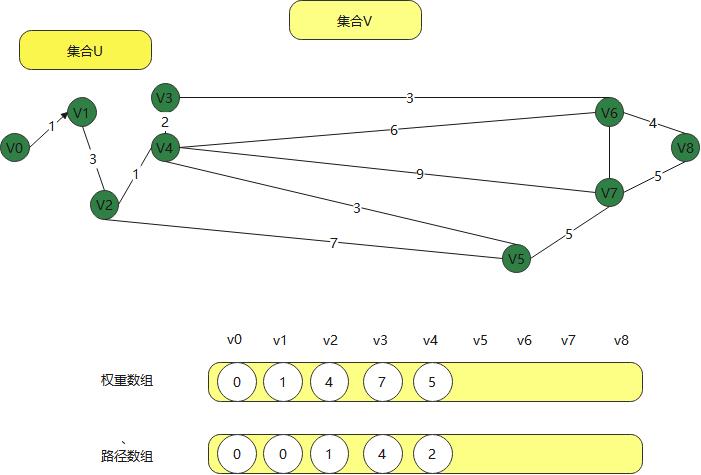
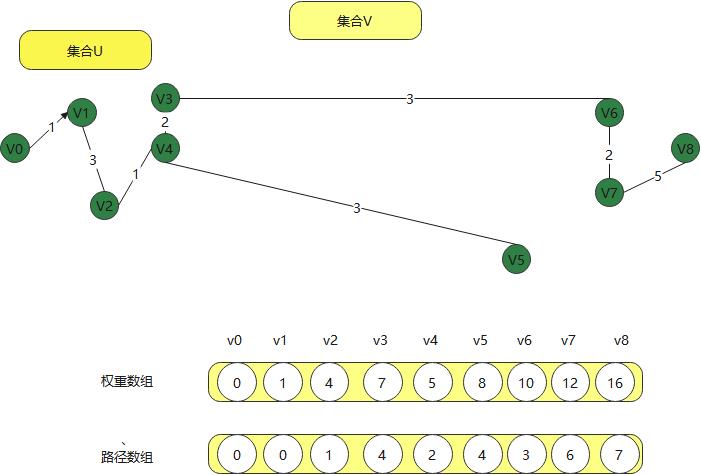
最后得到得到下面得权重和路径，

两个集合顶点，一直在计算和修正，这样就能找到一个顶点到后面顶点得最短路径，这就是迪杰斯特拉算法。

在代码中实现，是通过邻阶矩阵，左上进行看最大和最小。

代码实现

首先创建一个邻接矩阵

 public static final int I = 100;
    int[][] array=new int[][]{
            {0,1,5,I,I,I,I,I,I},
            {1,0,3,7,5,I,I,I,I},
            {5,3,0,I,1,7,I,I,I},
            {I,7,I,0,2,I,3,I,I},
            {I,5,1,2,0,3,6,I,I},
            {I,I,7,I,3,0,I,5,I},
            {I,I,I,3,6,I,0,2,7},
            {I,I,I,I,9,5,2,0,4},
            {I,I,I,I,I,I,7,4,0}
    };

处理顶点，首先要创建两个集合

 int k=0;//表示当前正要处理的顶点Vk
 //初始化相关的信息
 int[] path=new int[9];
 int[] weight=array[0];

 最开始表示v0智能到v1和v2,然后不断修正

 //定义一个数组来存放U和V两个集合的信息
        int[] flag=new int[9];

就开始逻辑进行修正数据了

 //开始逻辑,求VO到某个顶点的最短路径
        for(int v=1;v<9;v++){
            //在能走的路径中找到最短的一条
            int min=I;
            for(int i=0;i<9;i++){
                if(flag[i]==0 && weight[i]<min){
                    k=i;//K为U集合到V集合中找到的顶点
                    min=weight[i];//min找到了最小值的位置
                }
            }
            //从这个最短的路径对应的顶点开始找下一轮
            flag[k]=1;
            //修正当前最短路径
            for(int i=0;i<9;i++){
                //如果经过V顶点的路径比现在的路径短，新更新
                if(flag[i]==0 && (min+array[k][i])<weight[i]){
                    weight[i]=min+array[k][i];//修改路径长度
                    path[i]=k;//保存前驱
                }
            }
        }

按照之前得思路， 先选择 v0中最小权重得那个顶点，K为U集合到V集合中找到的顶点

 //在能走的路径中找到最短的一条
            int min=I;
            for(int i=0;i<9;i++){
                if(flag[i]==0 && weight[i]<min){
                    k=i;//K为U集合到V集合中找到的顶点
                    min=weight[i];//min找到了最小值的位置
                }
            }

从这个最短的路径对应的顶点开始找下一轮，这里得修正也是我们只会修正最上面行，weight 数组，以来保证最短的路径

 flag[k]=1;
            //修正当前最短路径
            for(int i=0;i<9;i++){
                //如果经过V顶点的路径比现在的路径短，新更新
                if(flag[i]==0 && (min+array[k][i])<weight[i]){
                    weight[i]=min+array[k][i];//修改路径长度
                    path[i]=k;//保存前驱
                }
            }

这里进行修正路径就是按照下面的方式进行修正，如果他下面的值加上左边的任意一个值，小于他就行修正，也就是min+array[k][i]<werght 则进行修改

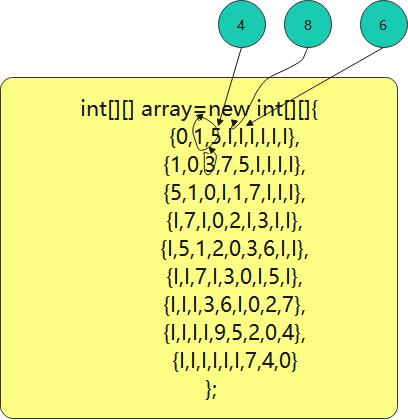
 也就是修正过后就为  [0,1,4,8,6,i,i,i,i],然后继续进行修正， 到2开始继续进行修正

就是继续标记下去，

flage[]={0,0,0,0....}

weight[]={0,1,5,i,i....}

path[]={0,0,0,0}

然后继续看下一行 {0,1,4,8,5,i,i,i,i}

int[][] array=new int[][]{
            {0,1,4,8,6,I,I,I,I},
           ,
            {5,1,0,I,1,7,I,I,I},
            {I,7,I,0,2,I,3,I,I},
            {I,5,1,2,0,3,6,I,I},
            {I,I,7,I,3,0,I,5,I},
            {I,I,I,3,6,I,0,2,7},
            {I,I,I,I,9,5,2,0,4},
            {I,I,I,I,I,I,7,4,0}
    };

 最后把值打印出来就行

   for(int i=0;i<path.length;i++){
            System.out.print(path[i]+" ");
        }
        System.out.println();
        for(int i=0;i<weight.length;i++){
            System.out.print(weight[i]+" ");
        }
//打印结果
        int v=8;
        while(v!=0){
            System.out.print(path[v]);
            v=path[v];
        }

在现实生活中如何去找到最短路径，我们可以提高效率这些

最小生成树

图论中的应用包括下面的最小生成树算法应用非常广泛，一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。 [1]  最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。

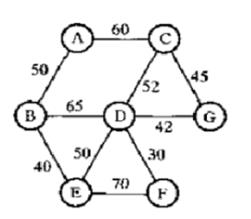
 克鲁斯卡尔(Kruskal) 算法

 

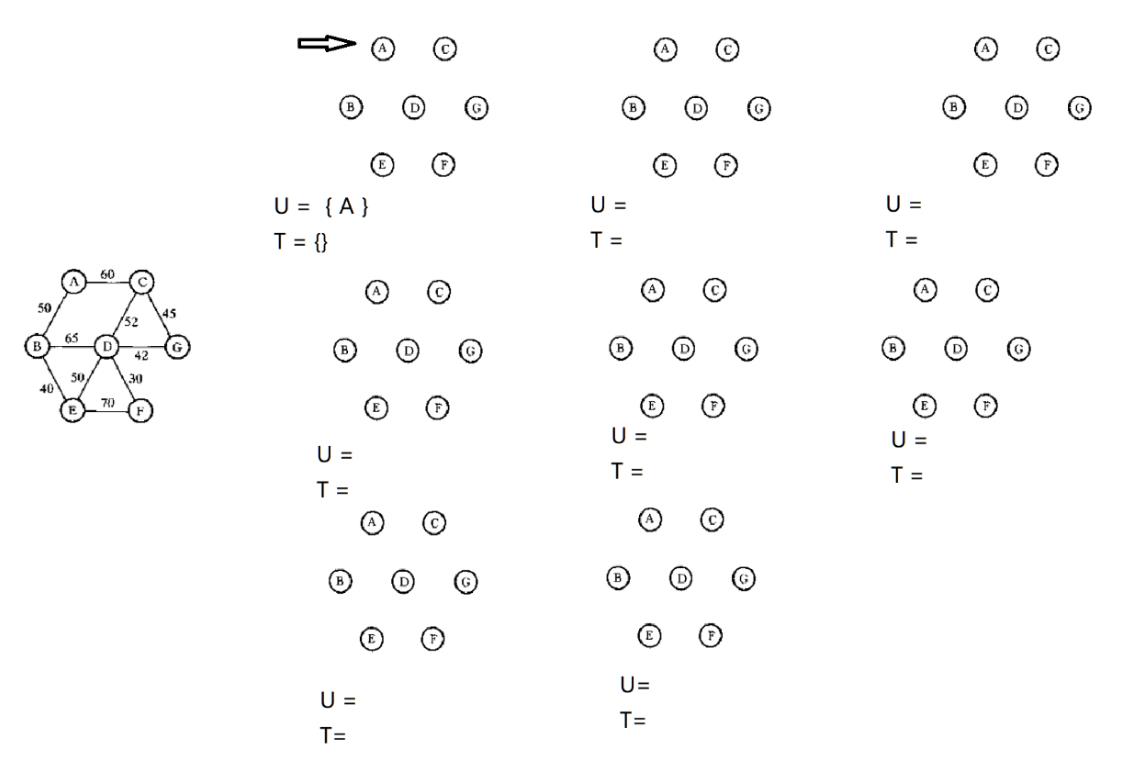
 这个算法也是图论算法中使用的，以边进行操作，点先进行排序，最小生成树

总结

图论的应用，弗洛伊德算法和迪杰斯特拉算法，的应用，都是为了寻找最短路径的。应用是相当广泛，提高程序性能，解决最短路径的问题，我们在学习这个算法，对提高自己技术是非常有用的。