论文笔记：On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima

Posted 2022-11-23 UQI-LIUWJ

 2017 ICLR

0 摘要

• 这篇文章探究了深度学习中一个普遍存在的问题——使用大的batchsize训练网络会导致网络的泛化性能下降（Generalization Gap）。
  • 大的batchsize训练使得目标函数倾向于收敛到sharp minima（local minima）
    • sharp minima导致了网络的泛化性能下降
  • 小的batchsize则倾向于收敛到一个flat minima

1 intro

• 一般的深度学习算法都是通过优化一个目标函数来训练网络参数的，这是一个非凸的优化问题。
  • 整个过程可以表达为下面的式子：
  • 
  • 其中M是数据的数量，f(x)就是损失函数/目标函数
• 一种常见的优化方法就是SGD
  • 
  • 这里Bk 是batchsize的大小，一般取值32,64，…,512
  • 经过实践的检验，这些常见的batchsize大小设置可以有以下的优点：
    • 收敛到凸函数的最小值点以及非凸函数的驻点；
    • 避免鞍点的出现
    • 对输入数据具有鲁棒性
       
• 但SGD有一个主要缺点，那就是并行化困难
  • 一个常见方法是增大batchsize，然而这导致了Generalization Gap的出现 

2 大batch的缺点

•  大Batch方法与小Batch方法在训练的时候实际上得到的目标函数的值是差不多的【只是在测试集上会有一定的gap】
• 这个现象的可能原因有下面几点（LB=Large-Batch；SB=Small-Batch）
  • LB方法过拟合模型;
  • LB方法被吸引到鞍点;
  • LB方法缺乏SB方法的探索性质，并倾向于放大最接近初始点的最小值;
  • SB和LB方法收敛到具有不同泛化特性的不同的最小化。
• 作者这篇文章主要研究的是后两点原因
  • 作者认为大Batch方法之所以出现Generalization Gap问题，原因是大Batch方法训练时候更容易收敛到sharp minima，而小Batch的方法则更容易收敛到flat minima。
  • 并且大Batch方法不容易从这些sharp minima的basins中出来。

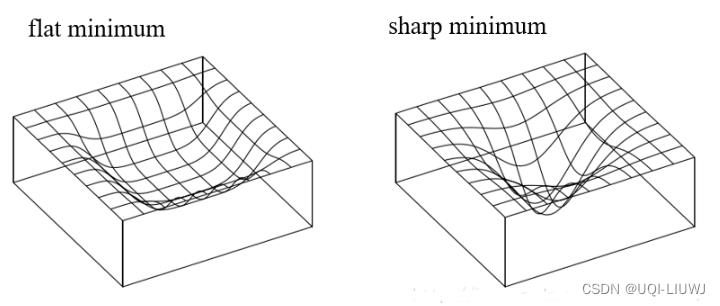
• 以上图为例，我测试集比训练集稍微偏离一点，如果是flat mininum的话，还会在最小值附近；但是如果是sharp mininum的话，那就离得远了

3 实验验证

3.1 数据集和网络结构

C1,C3——AlexNet结构

C2,C4——GoogleNet结构

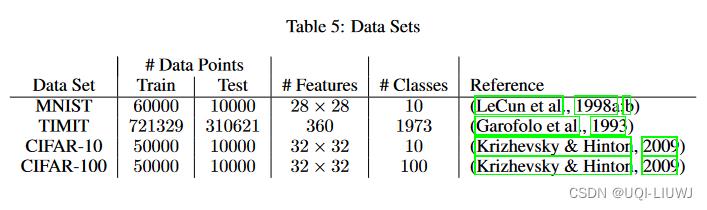
• 实验中LB方法的Batchsize定义为整个数据集的10%，SB方法的Batchsize定义为256。
• 优化器使用ADAM（ADAGRAD、adaQN等几个方法得到的结论是类似的）。
• 损失函数使用的是交叉熵形式。

 3.2 实验结果

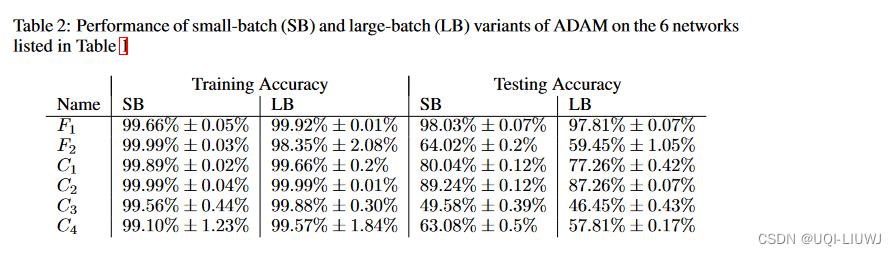
•  对应Table1中6个网络的实验的结果如table2所示。
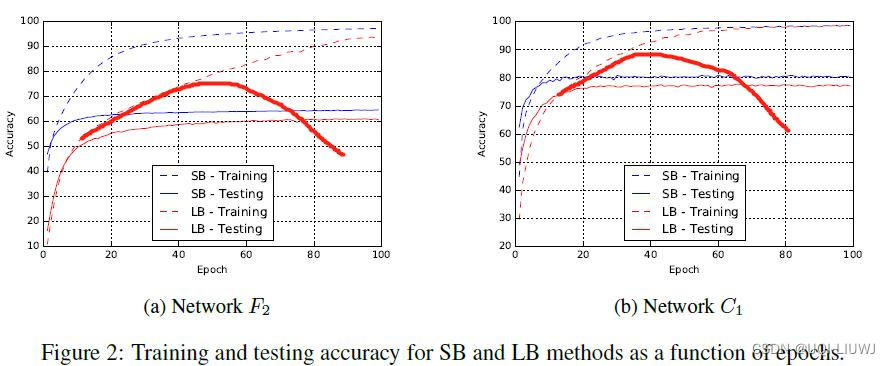
• 可以看到，SB和LB两种算法在Training阶段取得的结果非常相近，而Testing阶段LB方法明显出现了Generalization Gap的现象。

 

3.2.1 generation gap 并不是过拟合导致的

作者可视化了testing和training的training和testing loss

 

 此时testing上performance和training上的距离，并不是因为过拟合导致的。

如果是过拟合的话，个人觉得应该是这样的：

 3.2 minima的sharpness

3.2.1 直观可视化

• Figure3给出的是一维的参数曲线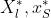，分别表示SB和LB方法在ADAM优化器中得到的预测结果，α在[-1,2]之间
  • α=0——>对应SB方法
  • α=1对应LB方法
  • α<0.5——>SB方法主导；α>0.5——>LB方法主导

  

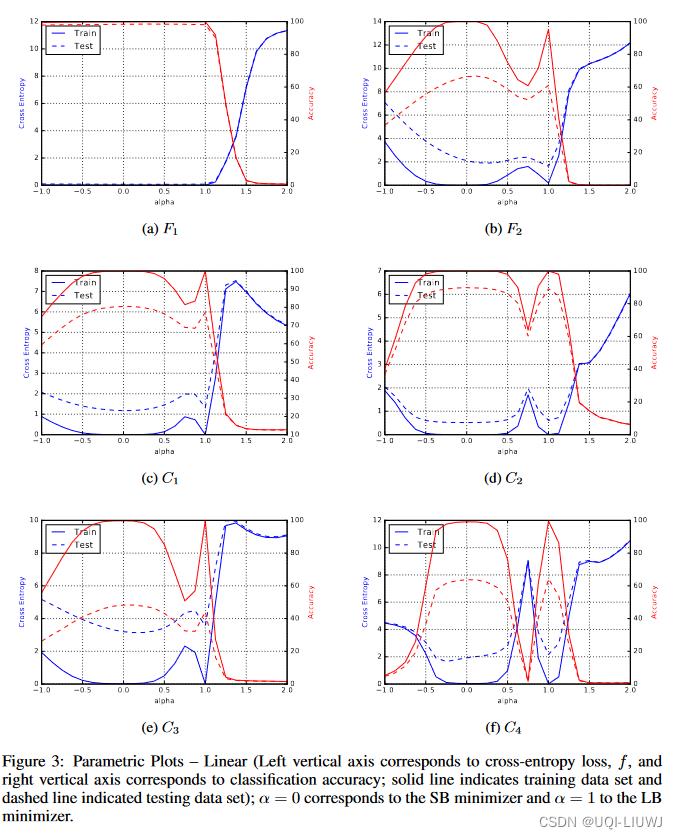
• 可以看到，在0.5左边（SB主导的时候），accuracy高，同时比较平缓；在0.5右边（LB主导的时候），accuracy低，同时比较陡峭 

3.2.2 sharpness定义

• 给定一个矩阵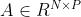，A是一个在全空间随机抽样产生的矩阵
• A+是矩阵A的伪逆
• 那么我们定义范围限定集为：
• 
• 其中epsilon控制了范围限定集的大小 

• 我们定义sharpness为：

3.2.3 各网络sharpness对比 

table3表示了整个空间上的最小值锋利度，而table4则是子空间（100维）。

3.3 模型效果随batch大小的变化 

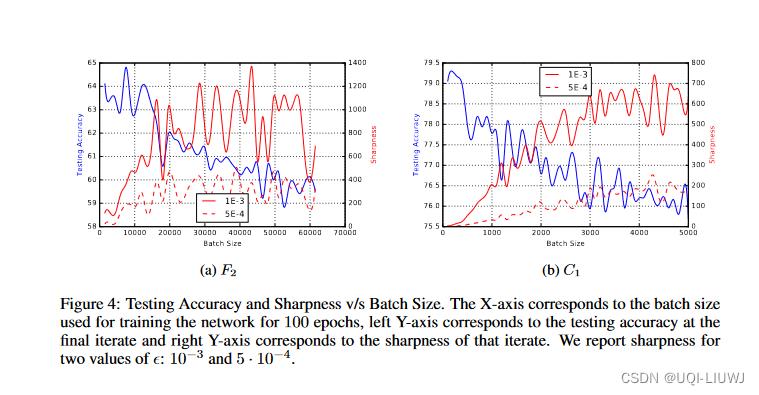
• 关于batchsize的选择是存在一个阈值的，batchsize大于这个阈值会导致模型质量的退化。
• 这个现象可以由figure4看出来，figure4中的F2的约15000和C1的约500，大于这个阈值网络准确度大幅下降

 

• SB方法使用的梯度具有内在的噪声，从实验以及经验来看，这些噪声使得SB方法的minimum在到达一个相对sharp的区域时，能够将最优值推出去，到达一个相对flat的区域。而这些噪声不足以将一个本来就很flat的minimum推出去。
• 而LB方法明显大于上面所说的阈值的时候，梯度内存在的噪声不足以将minimum推出sharp区域。