应用统计学简单随机抽样的区间估计和样本容量的确定

Posted 2022-11-17 古月书斋

一、置信度和置信区间

 

 二、总体均值的置信区间

1.总体服从正态分布，且方差已知

若随机变量X服从正态分布，那么它抽样分布的样本均值也服正态分布。同时，我们可以先将它转化为标准正态分布

根据区间估计的定义，我们可以构造总体均值μ的置信区间。对于给定的显著性水平α，有

 将式(5.13)代入上式得到:

 对上式括号内做不等式的等价变换后得到:

 

 于是置信度1- α置信区间μ的上下限是:

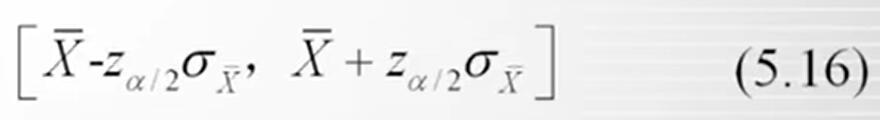
将放回抽样和不放回抽样的抽样平均误差的计算公式代入式(5.16)，可得置信度为1- α的总体均值置信区间公式:

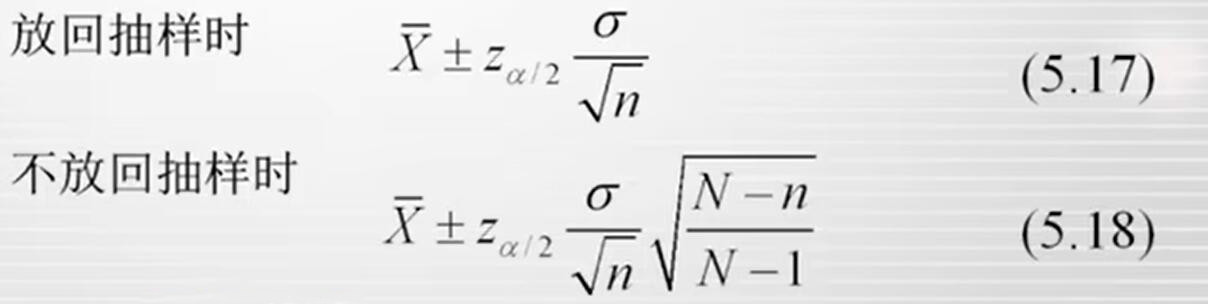
 例5-3 某银行想对本月银行储户提取的现金平均数做估计，现采用随机不放回抽样方式在现有的2000名客户中抽取400名储户的提现记录，测得样本的平均提现额度为1000元。已知储户提现额度服从正态分布，且标准差为150元。试以95%的置信度估计本月该行客户的提现平均额的置信区间。

 因此，在置信度95%下，该行储户的提现平均额度的置信区间为986.85元~1013.15元。

2.总体服从正态分布，但是方差未知

若随机变量X服从正态分布，但是方差未知，那么它抽样分布的样本均值也用类似于正态分布的T分布来进行近似计算。样本均值经过标准化以后，得到的随机变量服从自由度为n-1的t分布

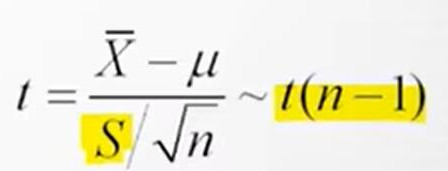
 同上，对于放回抽样和不放回抽样，置信度为1- α的总体均值的置信区间公式为:

例5-4

 

 

 3.非正态总体

对于总体非正态分布的情况，如果样本容量足够大（n>30）；那么对于方差已知，抽样分布的样本均值可用正态分布来进行近似计算。同理，对于方差未知，抽样分布的平均数可用类似于正态分布的T分布来进行近似计算。

 三、总体成数的置信区间

 同理，大样本情况下，总体成数的置信区间公式如下：

 例5.5 某保险公司欲了解本地区汽车保险的出险情况。随机抽查了100辆机动车过去一年的保单，其中有25份保单有出险记录。试以95%的置信度估计该地区汽车保险出险率的置信区间。

四、两个总体均值之差的置信区间

当总体服从正态分布时，根据正态分布再生定理，样本平均数服从正态分布。当总体不服从正态分布时,根据中心极限定理，当n充分大时(通常要求n≥30），样本平均数近似服从正态分布。所以，我们可以推断出：

 

 例5-6

 

例5-7 

 

 

 备注：5.30式需要大样本条件才成立，即一般要求样本数量n>=30.

五、两个总体成数之差的置信区间

例5-8

某饮料公司对其所做的报纸广告在两个城市的效果进行了比较，他们从两个城市中分别随机调查了1000个成年人，其中看过该广告的样本成数分别为0.18和0.14，试求两个城市成年人中看过该广告的成数之差的95%的置信区间。

六、 估计总体均值样本容量的确定

1、放回抽样

 例5-9

某企业想估计本企业职工上个月上下班花在路途上的平均时间。经验表明，总体标准为4.3分钟。以置信度95%的置信区间进行估计，并使估计值处在真正平均值附近1分钟的误差范围之内。该企业应抽取多大的样本?

  说明:当公式计算的结果带有小数时，样本容量应取比这个数大的最小整数。

2、不放回抽样

 七、 估计总体成数样本容量的确定

1、放回抽样

 例5-10

一家公司想估计某地区拥有彩色电视机的家庭所占的比例。该公司希望对的估计误差不超过0.05，要求置信度为95%，这时应取多大容量的样本?
解:根据相关知识，当P=0.5时，样本成数方差达到最大值。因此，在无法得到P值时，可以用P=0.5计算。这样得出的必要样本容量虽然可能比实际需要的容量大一些，但可以充分保证有足够高的置信水平和尽可能小的置信区间。

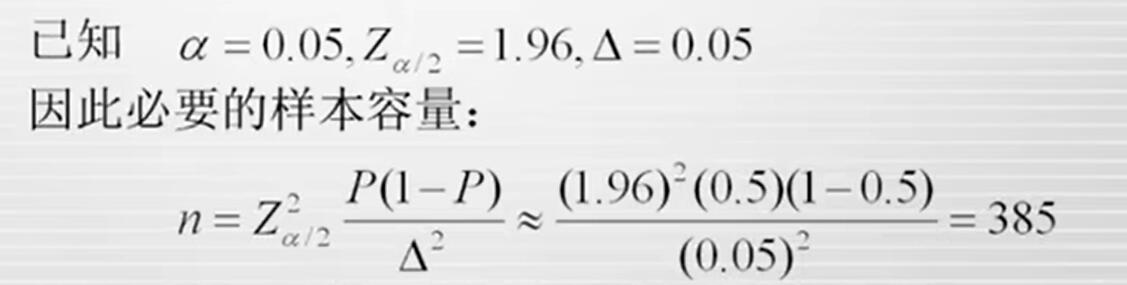
 故为了以95%的置信度保证估计误差不超过0.05，应取385户进行调查。

2、不放回抽样

同理，可由不放回抽样总体成数的置信区间估计公式推得:

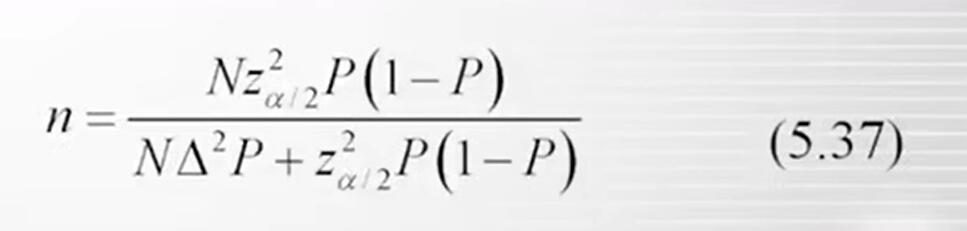
 其中的样本成数P代替了未知的总体成数。