数据结构—二叉树如何删除一个结点二叉树排序树和二叉搜索树的遍历

Posted 2022-11-15 之墨_

二叉树的删除与遍历操作

• 二叉树删除结点
• 遍历(二叉树)
• 遍历(二叉搜索树)

二叉树删除结点

考虑以下四种情况

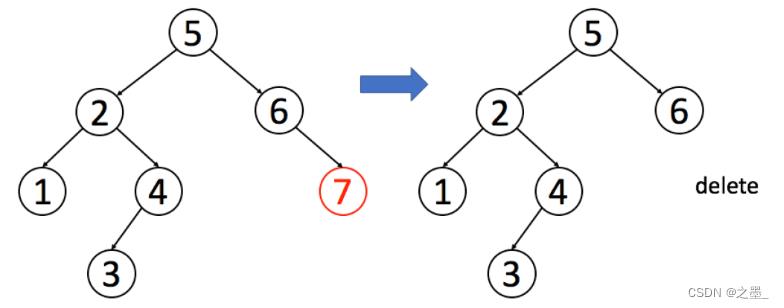
1. 被删除的节点是叶子节点
   直接删除

2. 被删除的节点仅仅有左孩子节点
   当被删除的节点仅仅有一个孩子时。用它的孩子节点，把它自己给替换下去。

3. 被删除的节点仅仅有右孩子节点
   与情况2类似

4. 被删除的有两个孩子节点

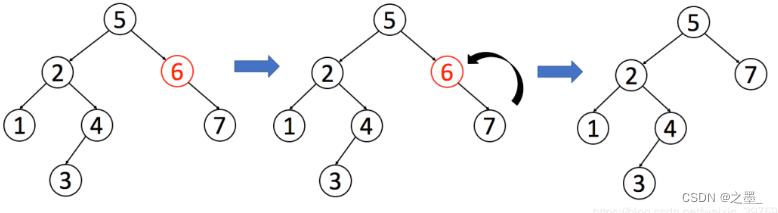
   1. 如果右孩子是叶子结点，那么右孩子直接替换被删结点
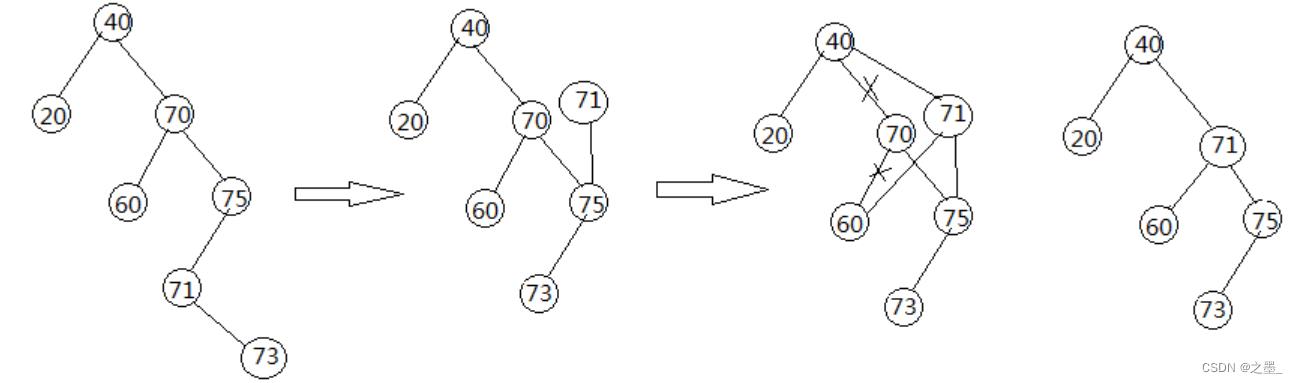
   2. 如果右孩子不是叶子结点，那么找到被删结点右子树中大于被删结点的最小结点，用这个最小结点替换被删结点，这个替换结点的父节点（及父节点的右子树) 变成替换结点的右子树，被删结点的左子树变成替换结点的左子树，替换结点的右子树变成其父节点的左子树，替换节点一定没有左子树，因为左子树会比替换节点更小且大于被删结点。

举个例子：


举个例子：
要在树中找出所有比被删除节点的值大的全部数。并在这些数中找出一个最小的数替换该被删结点。

遍历(二叉树)

注意！以下二叉树均指二叉排序树！

二叉排序树（Binary Sort Tree）或者是一棵空树；或者是具有下列性质的二叉树：

1. 若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 左、右子树也分别为二叉排序树；
4. 没有键值相等的节点；
   在经典教材《数据结构》严蔚敏 著 一书中 是不允许出现键值相同的节点的

二叉树的先序遍历：根——左子树——右子树
二叉树的中序遍历：左子树——根——右子树
二叉树的后序遍历：左子树——右子树——根
二叉树的层次遍历：从第一层开始，从上至下逐层遍历，在同一层中，则按照从左到右的顺序对节点逐个访问。

根据一棵树的先序遍历和中序遍历，或者后序遍历和中序遍历序列，都可以唯一地确定一棵树。

$(1)$先序序列与后序序列相同
空树或为只有根结点的二叉树

$(2)$中序序列与后序序列相同
空树或为任一结点至多只有左子结点的二叉树

$(3)$先序序列与中序序列相同
空树或为任一结点至多只有右子结点的二叉树

$(4)$中序序列与层次遍历序列相同
空树或为任一结点至多只有右子结点的二叉树

遍历(二叉搜索树)

“根据一棵树的先序遍历和中序遍历，或者后序遍历和中序遍历序列，都可以唯一地确定一棵树。”

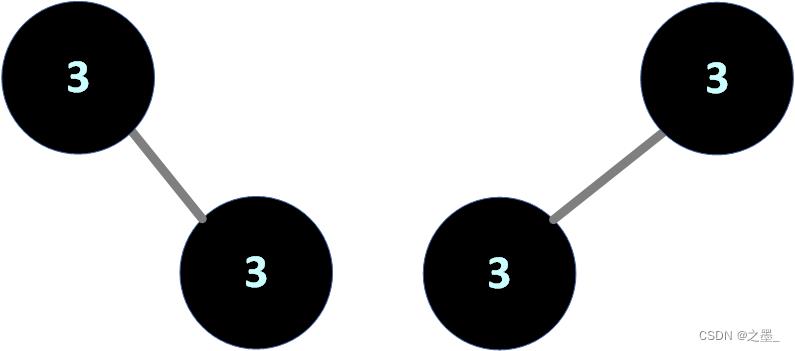
对于二叉搜索树不成立！，因为二叉搜索树允许相同键值的元素存在！

对于这两棵二叉搜索树，他们的前序后序中序遍历都是3、3，所以无法区分！

相同集合上的两棵二叉搜索树，若存在相同元素，则前序、后序或中序中的一种遍历相同，可能无法判断两棵二叉树搜索树相同。
若元素各异，可以确定唯一的一棵二叉搜索树。