t检验的前提是啥，需要大样本吗？

Posted 2023-04-30

参考技术A

T检验的前提是服从正态分布，跟下面所说一样，大样本是可以的，一般大于30就算大样本。补充：一般来说，如果两列数据每列数字的个数超过30个，可以默认其均值服从正态分布，直接用t配对检验。

单因素方差分析的前提是符合正态性，如果数据不符合正态性，可以将原数据进行转换，比如开根号，倒数，ln，log等，如果这样转换后还是不符合正态分布，那需要进行非参数检验。

扩展资料：

正态分布具有两个参数μ和σ^2的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N（μ,σ2）。

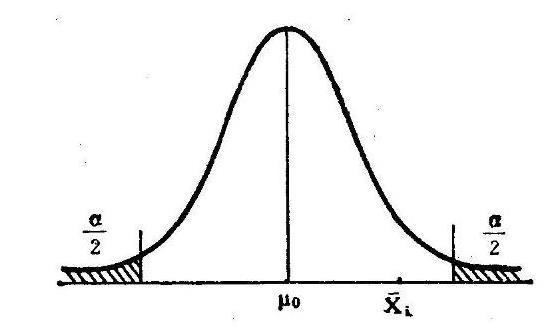
μ是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小。正态分布以X=μ为对称轴，左右完全对称。正态分布的期望、均数、中位数、众数相同，均等于μ。

σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。

参考资料来源：百度百科-正态分布

利用python库stats进行t检验

t检验通常分为三种，分别是单样本t检验、双样本t检验和配对样本t检验。本文基于python的scipy.stats函数对每种t检验进行了介绍和实验。

一、t检验介绍

无论哪种t检验，都有以下的基本前提条件：

1. 样本数据符合正态分布
2. 各个样本之间是独立的

步骤：

1. 提出原假设和备择假设
2. 构造t统计量
3. 计算t统计量
4. 对于得到的p值进行分析，p大于0.05则接受原假设，反之接受备择假设

二、 单样本t检验

应用场景：对某个样本的均值进行检验，比较是否和总体的均值(自己定）是否存在差异。

原假设和备择假设：

例如，我获取了50个中国人的身高（随机生成均值为1.5m的50个数据），想比较当前样本的平均身高和中国人的平均身高(1.7m）是否存在差异。按道理来说应该是存在差异的，因为一个是1.5,一个是1.7。

实现：使用ttest_1samp函数实现，第一个参数为样本数据，第二个参数为总体均值。代码如下：

from scipy.stats import ttest_1samp
from scipy import stats

rvs = stats.norm.rvs(loc=1.5, scale=1, size=(50)) 				# 生成均值为1.5，标准差为1的样本
t, p = ttest_1samp(rvs, 1.7)							# 进行单样本t检验

最终得到：

out：t =  -0.29277920321046647   p =   0.7709272063776454

p值大于0.05，说明我们不能拒绝原假设(即认为样本均值和总体均值没有显著差异)，说明样本的身高均值可以认为是1.7m。之所以得到这样的结果可能由于我们的样本数目太少，还有就是生成的数据1.5和1.7过于的接近。所以我们再进行一组实验来说明，将随机数的均值改为2.5。

rvs = stats.norm.rvs(loc=2.5, scale=1, size=(50)) 				# 生成均值为1.5，标准差为1的样本
t, p = ttest_1samp(rvs, 1.7)							# 进行单样本t检验，返回对应的t值和p值

得到：

out：t =  5.333243665065403  p =  2.4443516254546488e-06

此时p小于0.05，我们可以拒绝原假设(即认为样本均值和总体均值有显著差异)，说明样本身高的均值不可以认为是1.7m。而且因为2.5是大于1.7的，最终得到的t也是一个正数。

三、独立样本t检验(双样本t检验)

应用场景：是针对两组不相关样本（各样本量可以相等也可以不相等），检验它们在均值之间的差异。对于该检验方法而言，我们首先要确定两个总体的方差是否相等，如果不等，先利用levene检验，检验两总体是否具有方差齐性。

原假设和备择假设：

例如，我想检验A公司销售额的均值和B公司销售额的均值是否存在差异。

实现：使用stats.levene检验方差是否相等，再使用stats.ttest_ind进行独立样本t检验，代码如下：

A = stats.norm.rvs(loc=1, scale=1, size=(100))		 # 生成A公司的销售额
B = stats.norm.rvs(loc=3, scale=1, size=(100))		 # 生成B公司的销售额
stats.levene(A, B)					 # 进行levene检验

out:LeveneResult(statistic=0.8054648213132949, pvalue=0.37055445629183437)

得到的p值大于0.05，说明满足方差相等。使用ttest_ind函数进行独立样本t检验，函数的最后一个参数为判断两个样本的方差是否相同，如果不同，设为False进行独立样本t检验。

stats.ttest_ind(A,B,equal_var=True)				# 进行独立样本t检验
out：Ttest_indResult(statistic=-15.25297417258199, pvalue=2.993305057567317e-35)

检验结果显示p远小于0.05，我们拒绝原假设，即认为A公司和B公司的销售额均值存在显著差异

四、配对t检验

应用场景：是针对同一组样本在不同场景下均值之间的差异。检验的是两配对样本差值的均值是否等于0，如果等于0，则认为配对样本之间的均值没有差异，否则存在差异。

原假设和备择假设：

例如，我们有A公司今年的销售额以及去年的销售额，来判断今年和去年的销售额均值之间是否有差异。与独立样本t检验相比，配对样本T检验要求样本是配对的，两个样本的样本量要相同。

实现：可以选择单样本t检验的ttest_1samp函数(两组样本的差异为输入），也可以直接选择实现配对样本t检验的ttest_rel函数（两组样本作为输入)。代码如下：

A0 = stats.norm.rvs(loc=1, scale=1, size=(100))		 	 # 生成去年的销售额
A1 = stats.norm.rvs(loc=1.5, scale=1, size=(100))		 # 生成今年的销售额

# 计算两年销售额之间的差值
diff = A0-A1
# 使用ttest_1samp函数计算配对样本的t统计量
stats.ttest_1samp(diff)
out:
Ttest_1sampResult(statistic=13.983206457471795, pvalue=1.1154473504425075e-14)

# 使用ttest_rel函数计算配对样本的t统计量
stats.ttest_rel(A0,A1)
out:
Ttest_relResult(statistic=-4.731625986009621, pvalue=7.412846164679422e-06)

可见，用哪个函数最终得到的t和p值都是相同的。对于这个问题，p值小于0.05，认为两年的销售额存在显著差异。