已知两个线段的端点坐标如何用MATLAB求解他们之间的最短距离。要求的是线段啊，不是直线。

Posted 2023-04-27

最好可以贴出MATLAB源程序。谢谢。

t=3:0.01:5;
x=t;y=2*t;z=3*t;
t1=-1:0.01:2;
x1=t1;y1=2*t1;z1=3*t1;%以上是定义两条线段
n=length(t);
m=length(t1);
juli=zeros(n,m);
for i=1:n
juli(i,:)=sqrt((x1-x(i)).^2+(y1-z(i)).^2+(z1-z(i)).^2);%
end%获得每两个点之间的距离
[mina,mini]=min(juli(:));%找出距离中的最小值，及其单下标
j0=fix(mini/n)+1;
i0=mod(mini,n);%将单下标转化为双下标
x0=t(i0);y0=2*t(i0);z0=3*t(i0);
disp('点[x,y,z]=')
disp(x0)
disp(y0)
disp(z0)
x2=t1(j0);y2=2*t1(j0);z2=3*t1(j0);
disp('到点[x1,y1,z1]=')
disp(x2)
disp(y2)
disp(z2)
disp('为最短距离=')
disp(mina)%输出两点坐标，及最短距离
plot3(x,y,z,'r',x1,y1,z1,'r',x0,y0,z0,'b*',x1,y1,z1,'b*')
grid on%画出来
这个完全是用数值推出来的，精度受限于t与t1的步长，你懂的~~~ 参考技术A 1.绘制二维曲线的最基本函数plot
2.双纵坐标函数plotyy
3.
坐标控制
函数的调用格式为：
axis([xmin xmax ymin ymax zmin zmax])
axis函数功能丰富，常用的用法还有：
axis equal 纵、横坐标轴采用等长刻度
axis square 产生正方形坐标系(缺省为矩形)
axis auto 使用缺省设置
axis off 取消坐标轴
axis on 显示坐标轴
grid on/off命令控制是画还是不画网格线，不带参数的grid命令在两种状态之间进行切换。
box on/off命令控制是加还是不加边框线，不带参数的box命令在两种状态之间进行切换。
4.图形窗口的分割
subplot函数的调用格式为：
subplot(m,n,p)
5.绘制二维图形的其他函数
1. 其他形式的线性直角坐标图
在线性直角坐标系中，其他形式的图形有条形图、阶梯图、杆图和填充图等，所采用的函数分别是：
bar(x,y,选项)
stairs(x,y,选项)
stem(x,y,选项)
fill(x1,y1,选项1,x2,y2,选项2,…)
6.极坐标图
polar函数用来绘制极坐标图，其调用格式为：
polar(theta,rho,选项)
其中theta为极坐标极角，rho为极坐标矢径，选项的内容与plot函数相似。
7.对数坐标图形
MATLAB提供了绘制对数和半对数坐标曲线的函数，调用格式为：
semilogx(x1,y1,选项1,x2,y2,选项2,…)
semilogy(x1,y1,选项1,x2,y2,选项2,…)
loglog(x1,y1,选项1,x2,y2,选项2,…)
8.对函数自适应采样的绘图函数
fplot函数的调用格式为：
fplot(fname,lims,tol,选项)
9.绘制三维曲线的最基本函数
plot3函数与plot函数用法十分相似，其调用格式为：
plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n)
10.三维曲面
1．平面网格坐标矩阵的生成
(1)利用矩阵运算生成。
x=a:dx:b; y=(c:dy:d)';
X=ones(size(y))*x;
Y=y*ones(size(x));
(2)利用meshgrid函数生成。
x=a:dx:b; y=c:dy:d;
[X,Y]=meshgrid(x,y);
10.绘制三维曲面的函数
surf函数和mesh函数的调用格式为：
mesh(x,y,z,c)
surf(x,y,z,c)
标准三维曲面
sphere函数的调用格式为：
[x,y,z]=sphere(n)
cylinder函数的调用格式为：
[x,y,z]=sphere(R,n)
MATLAB还有一个peaks 函数，称为多峰函数，常用于三维曲面的演示。

11.其他三维图形
条形图、饼图和填充图等特殊图形，它们还可以以三维形式出现，使用的函数分别是bar3、pie3和fill3。此外，还有三维曲面的等高线图。等高线图分二维和三维两种形式，分别使用函数contour和contour3绘制。

怎么用matlab求解Logistic模型中的三个参数

给你这个实例，来说明如何用matlab求解Logistic模型中的三个参数。

x=[21 24 27 30 33 36 39 42 45 48];  %已知数值

y=[0 4.5541 11.5836 19.9043 22.7024 25.2441 26.2109 26.5693 26.6396 25.9511]; %已知数值

fun=inline('a(1)./(1+exp(a(2)-a(3).*x))','a','x');  %定义Logistic模型函数

a0=[0.95717  0.48538  0.80028]; %a的初值

a = nlinfit(x,y,fun,a0);  %求解Logistic模型中的三个参数

syms x

fx=vpa(fun(a,x),5);

str1=['拟合曲线f（x）：',char(fx)];

fprintf('%s\\n',str1)  %显示Logistic模型函数

运行结果

参考技术A 建立m函数文件存为logistic1
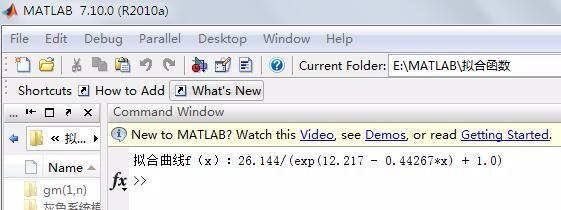
function f=logistic1(b)
t=[0,5,10,24,33,48,57,72,96,120,144,168,192,216];y=[0,0.028,0.103,0.336,0.450,0.597,0.716,0.778,0.835,0.849,0.816,0.839,0.811,0.816];
f = y-b(1)./(1+b(2).*exp(-b(3).*t));
b0=[10,2,2];
>> b=leastsq('logistic1',b0)
b =
0.8221 13.9173 0.0818
或者cftool
General model:
f(x) = b/(1+a*exp(-k*x))
Coefficients (with 95% confidence bounds):
a = 13.92 (6.301,21.53)
b = 0.822 (0.7911,0.853)
k = 0.08184 (0.06479,0.0989)
Goodness of fit:
SSE:0.01404
R-square:0.9898
Adjusted R-square:0.9879
RMSE:0.03572