RV32G下lui/auipc和addi结合加载立即数时的补值问题

Posted 2022-11-02 snsn1984

一、问题描述与解决思路

在32位下，lui/auipc通常用来取一个32位数的高20位，并且是带符号操作，将最高位默认为符号位。那么，取完最高位20位之后，再取低12位的时候，会面临一个补值问题。

假设这个32位内容为正数，lui/auipc取高20位的时候本身没问题，但是后续再对剩余的12位数字进行操作的时候，如果第11位是1，那么这一位会被当成是符号位，就将一个12位的正数变成了一个11位的负数。这种情况之下，lui/aupic和addi的合并操作的计算结果就不对了，就变成了高20位减去了一个低11位负数。正确的结果应该是高20位加上一个正的低12位。焦点就是将本不是符号位的第11位当成了符号位进行 处理。

《Computer Organization and Design》第五版RISCV版中，第114页中也讨论了这个问题：

在例子后面的讨论中提到了这个问题，解决方案是加上一个2的12次方，然后能保证得到一个正确的结果。

这里边的逻辑是这样的：一个12位的正数，它的值等于x11 * 2(11) + x10 * 2(10) + .... + x0 * 2(0)。这里x11指的是第11位上的数字，通常是1或者0，2(11)指的是2的11次方。但是如果这个12位的正数被当成了负数，而负数在这里使用补码表示的，那么它的值就等于 -x11 * 2(11) + x10 * 2(10)+ .... + x0 * 2(0)。加上12位正数和减去11位负数的差距就变成了（x11 * 2(11) + x10 * 2(10) + .... + x0 * 2(0)）-（-x11 * 2(11) + x10 * 2(10)+ .... + x0 * 2(0)）= 2 * x11 * 2(11)，而我们知道x11这时候是等于1的，那么这里就等于2(12)，也就是2的12次方。所以在这种情况之下，加上一个2的12次方，就可以保证结果正确了。

具体例子推导：
`

这个数等2(12)+2(11)+2(0)。
如果拆分的时候将后12位当成负数100000000001（补码）,这后12位数所对应的值就为-2(11)+2(0)，就是负的2(11)-2(0)，所对应原码111111111111（原码）.所以整个32位数的值就变成了2(12)-2(11)+2(0)，也即2(11)+2(0)。后者比前者少2(12).
注：2(x)表示2的x次方。
`

所以，这个问题的解决变成了要判断分开加载的这个32位正数的第11位是否为1，如果为1则需要加上2的12次方去保证正确结果，如果为0则不需要操作。

华为开源的[BishengJDK](https://gitee.com/openeuler/bishengjdk-11/tree/risc-v） 对RISCV64位进行了支持，其中有涉及到上述问题的解决，解决方法比较巧妙，这里拿来具体的例子进行介绍下。

二、代码实现

1. 方法一：

通过直接在auipc指令接受的立即数上加了一个0x800去解决该问题。0x800是2的11次方，这个2的11次方遇到立即数第11位为1的情况下，就会向立即数的第12位进1，等于补值已经完成了。遇到第11位为0，会为第11位加上1。但是，由于这里只取了第12位到第31位，后面的都丢弃掉了，所以不会对其他部分进行影响。
BishengJDK的处理方法：
src/hotspot/cpu/riscv64/assembler_riscv64.cpp

1)正数例子推导

`

这个数等于2(12)+2(11)+2(0)。 如果拆分的时候将低12位当成负数100000000001（补码）,这低12位数所对应的值就为-2(11)+2(0)，就是负的2(11)-2(0)。这时候，高20位的值为2(12)，二者合并之后，值变成了2(12)-2(11)+2(0)，和原来的值差了2*2(11)，就是2(12)。而+0x800的操作，可以让高20位的值变成2(12)+2(12)，就提前补齐了差值。

注：2(x)表示2的x次方。

`

2)负数例子推导

如果对这个问题进行扩展，进行处理的是32位的负数，会不会出现这个情况。如果在第11位为1的情况之下，也会出现这个情况，也需要加上2的12次方去保证运算结果。

具体例子推导：
`

因为这个数本身就是负数，所以这里是补码。通过补码可以直接计算出这个数等于-2(31)+2(12)+2(11)+2(0)。
如果拆分的时候将后12位当成负数100000000001（补码）,这后12位数所对应的值就为-2(11)+2(0)，就是负的2(11)-2(0)所以整个32位数的值就变成了-2(31)+2(12)-2(11)+2(0)，也即-2(31)+2(11)+2(0)。后者比前者少2(12).而+0x800的操作，可以让高20位的值变成-2(31)+2(12)+2(12)，就提前补齐了差值。
注：2(x)表示2的x次方。
`

2.方法二：

在拆分数据的时候，通过upper和lower的相减，提前为后续的二者组合补值。

BishengJDK的处理方法： src/hotspot/cpu/riscv64/assembler_riscv64.cpp

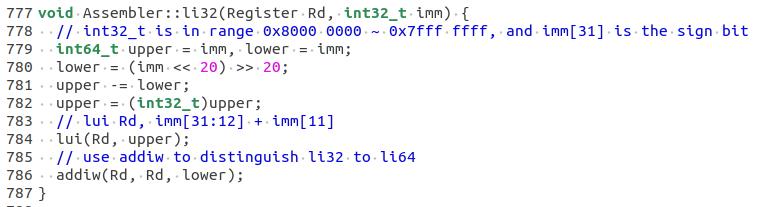
这里的lower等于imm左移20位右移20位，这种时候，第11位已经彻底的变成了符号位。upper -= lower，拆分完了之后，upper就等imm - lower，所以再组合的时候，imm = (imm - lower) + lower，这时候无论imm[11]是1还是0，lower是正数还是负数，结果都不会受影响了。

注释里写道“lui Rd, imm[31:12] + imm[11]”,其实也是在imm[11]为1的情况下，为imm[12]加上一个1，也就是加上一个2的12次方。这里的实际情况是，如果imm[11]为1，那么imm-lower的时候，会出现imm[11] + imm[11],也即2，这时候就会像imm[12]进1，就等于比imm[31:12]多了一个1，整数上就多了一个2的12次方。

1) 正数例子推导

`

这个数等于2(12)+2(11)+2(0)。 这时候，lower通过位移之后，变成了1111111111111111111110 0 0 0 0 0 0 0 0 0 1（-2(11) + 1），而upper=imm - lower，就成了2(12) + 2(11) + 2(11) = 2 * 2(12)，比imm[31:12]的2(12) 多了一个2(12)。这就完成补值，为后续合并imm已经做好了准备。在后续合并中，upper + lower = 2 *2(12) - 2(11) + 2(0) = 2(12)+2(11)+2(0)，这就和拆分前完全一致，证明补值完全有效。

注：2(x)表示2的x次方。

`

2) 负数例子推导

如果对这个问题进行扩展，进行处理的是32位的负数，方法二能不能有效。实际推导证明它依然是有效的。

具体例子推导：

`

因为这个数本身就是负数，所以这里是补码。通过补码可以直接计算出这个数等于-2(31)+2(12)+2(11)+2(0)。 这时候，lower通过位移之后，变成了1111111111111111111110 0 0 0 0 0 0 0 0 0 1（-2(11) + 1），而upper=imm - lower，就成了-2(31) + 2(13)，比imm[31:12]的-2(31) + 2(12)多了一个2(12)。这就完成补值，为后续合并imm已经做好了准备。在后续合并中，upper + lower = -2(31) + 2(13) - 2(11) + 2(0) = -2(31)+2(12)+2(11)+2(0)，这就和拆分前完全一致，证明补值完全有效。

注：2(x)表示2的x次方。

`

三、64位扩展

实际上，在64位立即数进行处理的时候，也会有这种情况发生。这就提醒我们在对一个数进行拆分然后再合并的时候，需要注意拆出来的后续字段最高位是否为1，因为这种情况下容易发生将数值本身当成符号位处理了。

感谢BishengJDK社区的小伙伴在该问题上的帮忙。

编辑于 05-25