SVM的简介

Posted 2022-11-02 纯纯的心儿

支持向量机，是一种非常好的算法，1992年提出，它的主要功能是分类和 回归。接下来我们讲的是分类方面的概念和应用。

支持向量机，即supportvector machine ，它可分为线性支持向量机和非线性支持向量机。在支持向量机的分类模型中，我们首要的目的就是去找到一个最大边缘超平面（具体的下面将会介绍）。而在最大超平面的两边，有一对分别平行于最大超平面的平面，要想找到最大超平面，就得找到这样的两个平面到这个最大边缘超平面的距离最大。（读起来有点拗口，下面将会以图形来展示）。

下面将以图形的方式介绍一下线性支持向量机的一些内容。（下面我们的案例都认为数据的线性可分的。）

图1

如图1所示，假如我们想把黑色的正方形和空白的圆形分开，那么我们就得找一条线把他们分开，这样的线有很多条。

但是要想使得分类效果好，如图2所示，

B1和B2这两条线都可以把他们分开，但是B1的边缘明显大于B2的边缘，所以，我们需要找一条有最大边缘的线，把二种图形分开的明显一些。为什么边缘大的分类效果就好呢？打个比方，很多的点都在b21的虚线周围，那么我们有时候就很难去分辨他该属于哪一个类，假设我们以B2为最大边缘超平面，一个黑色的正方形位于b21的右方0.0002毫米处，那这样一来这个正方形就属于原形了，而我们知道，现在是存在B1的线使刚才的那个黑色正方形归为到黑色正方形的类中的，那么如果以B2为最大边缘超平面，这样就分类错误了。总的来说，寻找到一个最大边缘超平面的作用就是使得分类的误差达到最小。

那么，我们怎么样去找这样满足高分类效果的线呢？

下面我们将用函数的形式给出说明：

我们将线性支持向量机的最大边缘超平面写成如下的函数形式：

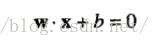
W和b是这个分类模型的两大参数。

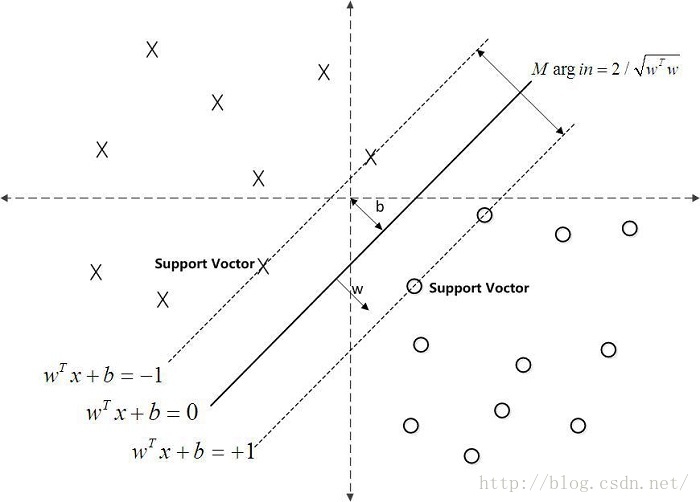
图3

如图3所示，中间的那条实线为决策边界（就是上面所说的超平面），我们令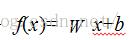

，当f（x）=0的时候，为决策边界。当f(x)=1或f(x)=-1的时候，为两个平行于决策边界的超平面，而在这两个超平面上面的点也就是支持向量。我们需要这俩个超平面到这个决策边界的距离最大，那么我们将转化到下面的式子：

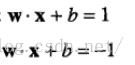
。两式相减，我们将得到,

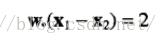
然后转化为 

，其中 ||W||为欧几里得范数，||W||=根号下（w*w）（这里作为了解下）。因此，我们得到的d为最大的边缘。那么也可以得到我们需要最小的||W||，使得最大化的d。

从上面的说的，我们可以知道，W是我们关键找的一个向量，在支持向量机的训练过程中，主要是获得w，一旦我们有了一个训练后的支持向量机（这个向量机保证了最大的边缘超平面，使得在此数据集下有较好的分类精度）。我们就可以用对于的SVM来对线性可分的数据进行分类。。。。。然后给上面训练后的支持向量机一个名称，为线性支持向量机。

所以，学习训练后的分类器的复杂度由支持向量的数目而不是由数据的维数来刻画。

 

好，到此为止，我们可以简单的了解了支持向量机的一个分类方式和分类的要求，也差不多能学会去怎么进行一个分类，但是我们没有了解他是怎么去训练的，这个我们可以不知道，因为太复杂。然后我们来看点高级的分类。

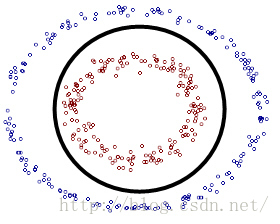
如图所示，

 

这么一个大圆包小圆，我们怎么去找一个超平面去把他们分成2类，如果你按照平面的思想，如果是加一条线割来割去，肯定是割不出头的。那么，我们就会想把他们放到空间里面去，对，就是这样。

我们可以看见，把这2沱 圆放在了空间里面，其实就是重新 把他们换了种方式进行表达，z*z=x*x+y*y;

这样就放空间里面去了嘛。

然后，既然是三维空间了，那么找一个超平面还不简单啊，看，在它旋转的时候，是不是2层之间是有空隙的，那么我们给他来一刀，那样，不就产生超平面了吗。然后我们怎么去砍，也就是类似于二维那样，怎么去找一条最优的线，使得分类的精度最大。割了一刀后，其实图就这样：

  而这里的圆其实在空间里面是一个平面而已。

 

好了。。这样，我们就把分类从平面放到了空间，具体怎么分类的，这样就涉及到了高维的拉格朗日推导和核函数的使用，这里不做具体的介绍。

  

接下来，我们讲一下SVM的运用，

 

根据SVM他可以进行分类，那么在这里我举个 P2P网络借贷的信用评估问题，在这里我提一下，就是现在的这个问题的支持向量机是非线性的。

 

我将举一个支持向量机运行在信用评估的例子。

因为在P2P网贷过程中，每个用户将会提交自己的信用信息，如 收入、年龄、婚姻状态等一系列的因素，而用户上交有些数据是不靠谱的，所以会造成管理者无法判断该用户是否违约，然后我们需要用支持向量机对其进行一个分类，判断其违约还是不违约。然后，看附件，有一份德国的网贷数据。

说明下数据的意思，最后的一列是输出，0 和 1  ，代表不违约或者违约，前面的所有列均为用户的信息，不过此数据已经经过数据预处理，共1000条，我们拿此来做一个训练。1000维数据中，我们拿1-650条数据进行训练，

[alpha,b]=trainlssvm(Pt1,Tt1,type,gam,sig2,'RBF_kernel','preprocess');

这一行是matlab中的代码，Pt1,Tt1分别为真实输入和真实输出，type类型是分类，gam和sig2是支持向量机的惩罚参数和核函数的参数，作约束用的，RBF_kernel是核函数，将高维的数据进行降维，'preprocess'指是数据预处理过的，代表数据的特性。

 

这个核心代码进行了支持向量机的训练，训练出来后，得到前面所述的W和b ，然后，我们需要检验这个训练后得到的那个超平面的效果，即我们可以用剩下的350条数据进行一个测试，

R=simlssvm(Pt1,Tt1,type,gam,sig2,'RBF_kernel','preprocess',alpha,b,P1);

最后的P1是测试的输入数据。

R是一行数据中得到的测试输出，因为在数据中，我们最后有一维是真实的违约情况，现在得到测试的分类，然后将测试的和真实的进行一个对比，这样，我们可以判断这个分类到底有多少是正确的，也就确定了分类的准确性。

以上就是 简单的一个 SVM的 应用， 差不多就这样了，

 

上面的支持向量机在高维分类的推导没讲，有兴趣的自己去看这个http://blog.pluskid.org/?p=685&cpage=1#comment-4697

 

详细的。。

欢迎评论！！！！！