最小马氏距离分类器
Posted yuyaweibest
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最小马氏距离分类器相关的知识,希望对你有一定的参考价值。
摘要:本次实验的第一部分是计算三类样本中每一类样本的均值矢量和协方差矩阵(假设每一类均为正态分布),编写计算马氏距离函数,用不同的颜色在一个图上分别画出这三个类在马氏距离分别为D=1、2、3时的图形,并且为这三个类别的分类设计一个最小马氏距离分类器。第二部分是编写最小马氏距离分类器、最小欧氏距离分类器和贝叶斯分类器函数,分别对四个测试点进行分类,并对分类结果进行对比分析。
一、 技术论述
1、马氏距离
考虑一个由d维向量x组成的样本集合X,若该集合中的样本x服从均值为m,协方差矩阵为S的多元高斯分布,其表达式如下所示:

马氏距离是用来表示数据的协方差距离,它是一种有效的计算两个未知的样本集的相似度的方法,考虑到了各个特性之间的联系。它的原理是通过计算向量x到每一个类均值向量的马氏距离,将x归于离它最近的均值所属的类。
2、最小马氏距离分类器

称上述为最小马氏距离分类器。
3、最小欧式距离分类器
欧式距离的定义为:
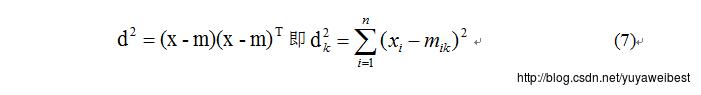
最小欧式距离分类器需要计算均值向量,判定样本归属于最小欧式距离所在的类别。最小欧氏距离分类法原理简单,容易理解,计算速度快,但是因为其只考虑每一类样本的均值,而不用管类别内部的方差(每一类样本的分布),也不用考虑类别之间的协方差(类别和类别之间的相关关系),所以分类精度不高,因此,一般不用它作为对精度有高要求的分类,但它可以在快速浏览分类概况中使用。
4、最小错误率贝叶斯分类器
利用贝叶斯公式对样本进行分类的分类器称为最小错误率贝叶斯分类器,考虑c类样本,令分类器函数为:
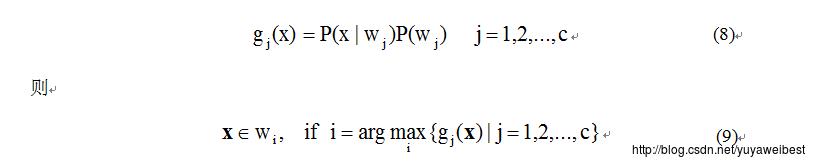
称上述为最小错误率贝叶斯分类器。
5、分类器分类步骤
(1)确定类别m,并提取每一类所对应的已知的样本。
(2)从样本中提取出一些可以作为区分不同类别的特性,也就是我们通常所说的特征提取,如果提取出了n个不同的特性,那么我们就叫它n维空间,特征提取对分类的精度有重大的影响。
(3)分别计算每一个类别的样本所对应的特征,每一类的每一维都有特征集合,通过集合,可以计算出一个均值向量和协方差矩阵,也就是特征中心。
(4)通常为了消除不同特征因为量纲不同的影响,我们对每一维的特征,需要做一个归一化,或者是放缩到(-1,1)等区间,使其去量纲化。
(5)利用选取的距离准则,对待分类的本进行判定。
二、 实验步骤及实验结果
1、基本实验
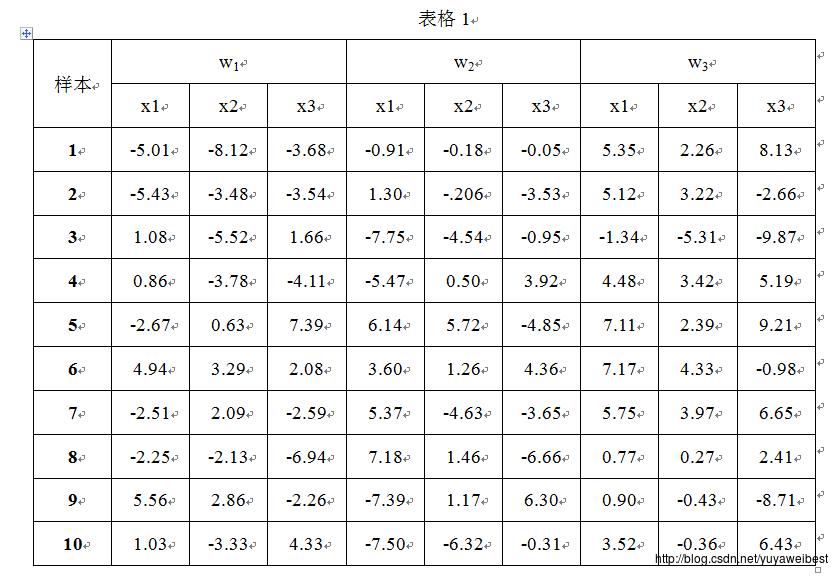
(a) 表格1为三类样本中的10个样本点,假设每一类均为正态分布。计算每一类样本的均值矢量和协方差矩阵,得到的协方差为3*3的矩阵;用不同的颜色在一个图中分别画出这三个类在马氏距离分别为D=1,2,3时的图形,为这三个类别的分类设计一个最小马氏距离分类器。实验结果如图1所示:
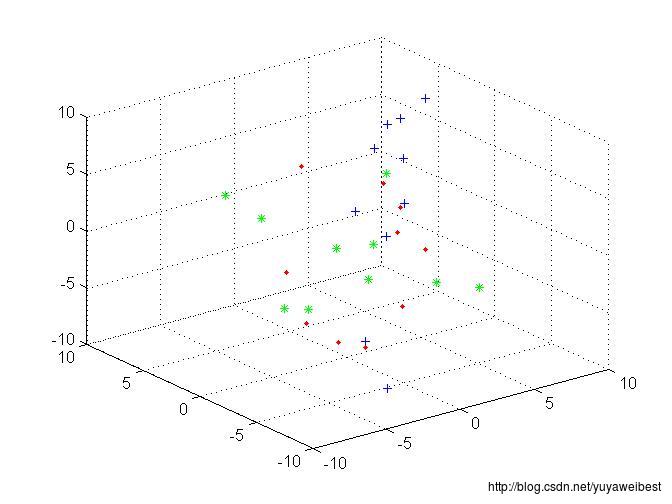
图1.三类样本点(RGB颜色分别代表第一、二和三类样本)

图2.第1类样本点分别在马氏距离D=1,2,3时的图形

图3.第2类样本点分别在马氏距离D=1,2,3时的图形
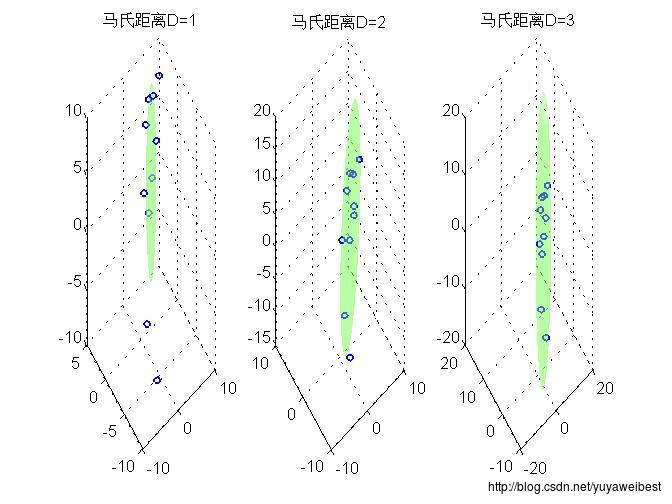
图4.第3类样本点分别在马氏距离D=1,2,3时的图形


2、 扩展实验
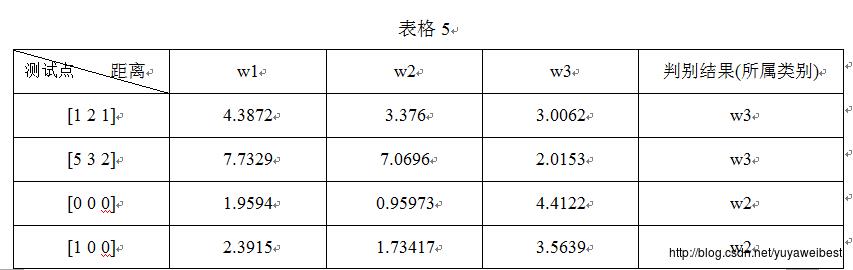
(c) 对上述基本实验中(b)的测试点,分别计算它们到各个类中心的欧氏距离。若使用最小欧氏距离对它们进行分类,将分类结果与(b)中的最小马氏距离分类器的结果进行比较。得到实验结果如下表所示:
将马氏距离的计算公式(2)中的协方差矩阵S^-1去掉后,得到的分类结果与最小欧式距离分类的结果是一致的,如下表所示:

三、 讨论与分析
1.由实验可得,使用最小马氏距离分类的结果是:点 (1,2,1)T ,(0,0,0)T,(1,0,0)T属于第2类,而 (5,3,2)T属于第3类;使用最小欧式距离分类的结果是:点 (1,2,1)T, (5,3,2)T属于第3类,而 (0,0,0)T,(1,0,0)T属于第2类;使用贝叶斯分类器分类的结果是:点 (1,2,1)T属于第2类,点 (5,3,2)T属于第3类,而点 (0,0,0)T,(1,0,0)T, 属于第1类。
2.马氏距离又称样本X到均值的平方Mahalanobis距离。等密度分布的边界是一些到均值m的恒定马氏距离的超椭球体,且这些超椭球体的体积决定了均值附近的样本的离散程度,对于一给定的维数,样本的离散程度直接随协方差矩阵|S|^(1/2)而变化。
3.采用最小欧式距离分类器不需要计算方差和协方差,欧氏距离将样本的不同属性之间的差别同等看待,而马氏距离是表示数据的协方差距离,是一种有效的计算两个未知样本集的相似度的方法,与欧式距离不同的是它考虑到了各种特性之间的联系。
由公式(2)和公式(7),比较表格5、6和7内的数据可知,当样本协方差矩阵的逆矩阵不存在时,欧式距离分类器来代替马氏距离分类器。当不需要考虑样本的协方差矩阵,使用最小马氏距离分类器等价于最小欧式距离分类器。
4.最小马氏距离分类器和贝叶斯分类器的结果有差别,因为两者采用的判别函数不一样,前者使用的是计算向量x到每一个类均值向量的马氏距离,将x归于离它最近的均值所属的类。后者使用的是计算x的后验概率,选择具有最大后验概率的类作为该对象所属的类,但必须知道先验概率。
附录
%主函数
close,close all;
w1=[-5.01,-8.12,-3.68;-5.43,-3.48,-3.54;1.08,-5.52,1.66;0.86,-3.78,-4.11;-2.67,0.63,7.39;...
4.94,3.29,2.08;-2.51,2.09,-2.59;-2.25,-2.13,-6.94;5.56,2.86,-2.26;1.03,-3.33,4.33];
w2=[-0.91,-0.18,-0.05;1.30,-.206,-3.53;-7.75,-4.54,-0.95;-5.47,0.50,3.92;6.14,5.72,-4.85;...
3.60,1.26,4.36;5.37,-4.63,-3.65;7.18,1.46,-6.66;-7.39,1.17,6.30;-7.50,-6.32,-0.31];
w3=[5.35,2.26,8.13;5.12,3.22,-2.66;-1.34,-5.31,-9.87;4.48,3.42,5.19;7.11,2.39,9.21;...
7.17,4.33,-0.98;5.75,3.97,6.65;0.77,0.27,2.41;0.90,-0.43,-8.71;3.52,-0.36,6.43];
figure(1);
plot3(w1(:,1),w1(:,2),w1(:,3),'r.');%用红色画出第一类数据点
hold on
plot3(w2(:,1),w2(:,2),w2(:,3),'g*');%用绿色画出第一类数据点
hold on
plot3(w3(:,1),w3(:,2),w3(:,3),'b+');%用蓝色画出第一类数据点
grid on
mu1=sum(w1)./10;%求第一类均值
mu2=sum(w2)./10;%求第二类均值
mu3=sum(w3)./10;%求第三类均值
for i=1:3
for j=1:3%分别求第一、二、三类的协方差分别为sigma1,sigma2,sigma3
sigma1(i,j)=sum((w1(:,i)-mu1(:,i)).*(w1(:,j)-mu1(:,j)))./9;
sigma2(i,j)=sum((w2(:,i)-mu2(:,i)).*(w2(:,j)-mu2(:,j)))./9;
sigma3(i,j)=sum((w3(:,i)-mu3(:,i)).*(w3(:,j)-mu3(:,j)))./9;
end
end
figure(2)%绘制第1类数据下,不同马氏距离的图形
subplot(131);
plot3(w1(:,1),w1(:,2),w1(:,3),'r.','markersize',4);
ma_plot(mu1,sigma1,1);%绘制马氏距离为1的图形
subplot(132);
plot3(w1(:,1),w1(:,2),w1(:,3),'r.','markersize',4);
ma_plot(mu1,sigma1,4);%绘制马氏距离为2的图形
subplot(133);
plot3(w1(:,1),w1(:,2),w1(:,3),'r.','markersize',4);
ma_plot(mu1,sigma1,9);%绘制马氏距离为3的图形
figure(3) %绘制第2类数据下,不同马氏距离的图形
subplot(131);
plot3(w2(:,1),w2(:,2),w2(:,3),'g*','markersize',4);
ma_plot(mu2,sigma2,1);%绘制马氏距离为1的图形
subplot(132);
plot3(w2(:,1),w2(:,2),w2(:,3),'g*','markersize',4);
ma_plot(mu2,sigma2,4);%绘制马氏距离为2的图形
subplot(133);
plot3(w2(:,1),w2(:,2),w2(:,3),'g*','markersize',4);
ma_plot(mu2,sigma2,9);%绘制马氏距离为3的图形
figure(4)%绘制第3类数据下,不同马氏距离的图形
subplot(131);
plot3(w3(:,1),w3(:,2),w3(:,3),'bo','markersize',4);
ma_plot(mu3,sigma3,1);%绘制马氏距离为1的图形
subplot(132);
plot3(w3(:,1),w3(:,2),w3(:,3),'bo','markersize',4);
ma_plot(mu3,sigma3,4);%绘制马氏距离为2的图形
subplot(133);
plot3(w3(:,1),w3(:,2),w3(:,3),'bo','markersize',4);
ma_plot(mu3,sigma3,9);%绘制马氏距离为3的图形
Pw=[1/3;1/3;1/3];
x1=[1,2,1];
x2=[5,3,2];
x3=[0,0,0];
x4=[1,0,0];
mu=[mu1;mu2;mu3];
sigma=[sigma1;sigma2;sigma3];
ma_classify(x1,mu,sigma);%调用最小马氏距离分类器函数,将测试点进行分类
ma_classify(x2,mu,sigma);%调用最小马氏距离分类器函数,将测试点进行分类
ma_classify(x3,mu,sigma);%调用最小马氏距离分类器函数,将测试点进行分类
ma_classify(x4,mu,sigma);%调用最小马氏距离分类器函数,将测试点进行分类
euclidean_classify(x1,mu);%调用欧氏距离分类器函数,将测试点进行分类
euclidean_classify(x2,mu);%调用欧氏距离分类器函数,将测试点进行分类
euclidean_classify(x3,mu);%调用欧氏距离分类器函数,将测试点进行分类
euclidean_classify(x4,mu);%调用欧氏距离分类器函数,将测试点进行分类
bayes_classify(x1,mu,sigma,Pw);%调用贝叶斯分类器,将测试点进行分类
bayes_classify(x2,mu,sigma,Pw);%调用贝叶斯分类器,将测试点进行分类
bayes_classify(x3,mu,sigma,Pw);%调用贝叶斯分类器,将测试点进行分类
bayes_classify(x4,mu,sigma,Pw);%调用贝叶斯分类器,将测试点进行分类
%绘制三维椭球面
function ma_plot(mu,sigma,D )
%数据拟合成一个曲面
insigma=inv(sigma);
[x,y,z]=meshgrid(linspace(-20,20));%生成网格
v=(((x-mu(1,1)) * insigma(1,1) + (y-mu(1,2))* insigma(2,1) +(z-mu(1,3))* insigma(3,1)) .* (x-mu(1,1)))+(((x-mu(1,1)) * insigma(1,2) +(y-mu(1,2))* insigma(2,2) +(z-mu(1,3))*insigma(3,2)) .*(y-mu(1,2)))+ (((x-mu(1,1))* insigma(1,3) + (y-mu(1,2))* insigma(2,3) +(z-mu(1,3))*insigma(3,3)) .*(z-mu(1,3)));
isosurface(x,y,z,v,D);%使用isosurface函数画出等值面
alpha .4;%设置透明度
grid on;
view(3);
title(['马氏距离为D=',num2str(sqrt(D))]);
end
%最小马氏距离分类器函数
function ma_classify(x,mu,s)
%ma_classify为函数名,利用最小马氏距离进行分类
%x为测试的点,mu为均值向量,s是为协方差矩阵
for i=1:3
r(i)=sqrt((x-mu(i,:))*inv(s(i*3-2:i*2+i,:))*(x-mu(i,:))');
disp(['测试点[',num2str(x),']到第一类的马氏距离为:',num2str(r(i))]);
end
[r_min,c]=min([r(1);r(2);r(3)]);%r_min保存程序的最小值,c为最小值所在行
disp(['判断结果:点[',num2str(x),']属于',num2str(c),'类']);
end
%最小欧式距离分类器函数
function euclidean_classify(x,mu)
%euclidean_classify函数,利用欧式距离对测试点进行分类
%x为测试的点,mu为均值向量
for i=1:3
d(i)=sqrt(sum((x-mu(i,:)).^2));
disp(['测试点[',num2str(x),']到第一类的欧氏距离为:',num2str(d(i))]);
end
[d_min,c]=min([d(1);d(2);d(3)]);%d_min保存程序的最小值,c为最小值所在行
disp(['判断结果:点[',num2str(x),']属于',num2str(c),'类']);
end
%贝叶斯分类器函数
function bayes_classify( x,mu,s,Pw )
%bayes_classify函数,利用贝叶斯分类器对测试点进行分类
%x表示输入的测试点,mu表示均值矢量,s表示协方差矩阵,Pw表示先验概率矩阵
for i=1:3
b(i)=Pw(i,:)*mvnpdf(x,mu(i,:),s(i*3-2:i*2+i,:));
disp(['测试点[',num2str(x),']对第一类的贝叶斯判别值:',num2str(b(i))]);
end
[b_max,c]=max([b(1);b(2);b(3)]);%b_max保存程序的最大值,c为最小值所在行
disp(['判断结果:点[',num2str(x),']属于',num2str(c),'类']);
end
以上是关于最小马氏距离分类器的主要内容,如果未能解决你的问题,请参考以下文章