算法快速排序

Posted 2023-02-18 sysu_lluozh

快速排序(Quicksort)，又称划分交换排序(partition-exchange sort)

算法思想

采用"分而治之"的思想，把大的拆分为小的，小的拆分为更小的。对于给定的记录，选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列

实现逻辑

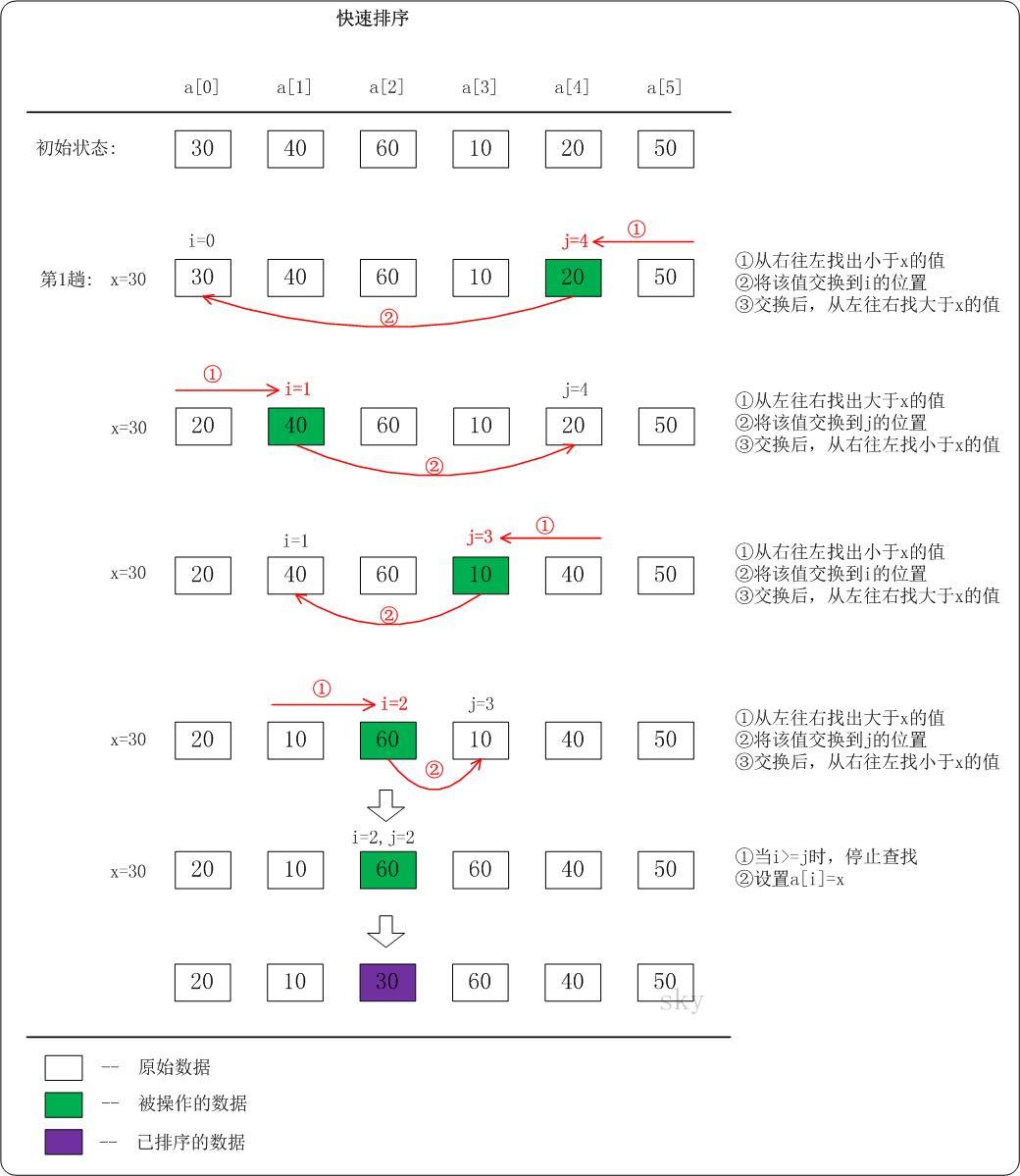
设当前待排序序列为R[low:high]，其中low ≤ high，如果待排序的序列规模足够小，则直接进行排序，否则分3步处理

1. 分解

在R[low:high]中选定一个元素R[pivot]，以此为标准将要排序的序列划分为两个序列R[low:pivot-1]与R[pivot+1：high]，并使序列R[low:pivot-1]中所有元素的值小于等于R[pivot]，序列R[pivot+1：high]所有的值大于R[pivot]，此时基准元素以位于正确位置，它无需参加后续排序

2. 递归

对于子序列R[low:pivot-1]与R[pivot+1：high]，分别调用快速排序算法来进行排序

3. 合并

由于对序列R[low:pivot-1]与R[pivot+1：high]的排序是原地进行的，所以R[low:pivot-1]与R[pivot+1：high]都已经排好序后，不需要进行任何计算，就已经排好序

注：基准元素，一般来说选取有几种方法

• 取第一个元素
• 取最后一个元素
• 取第中间位置元素
• 取第一个、最后一个、中间位置3者的中位数元素

实现代码

def quick_sort(alist, start, end):
    """快速排序"""

    # 递归的退出条件
    if start >= end:
        return

    # 设定起始元素为要寻找位置的基准元素
    mid = alist[start]

    # low为序列左边的由左向右移动的游标
    low = start

    # high为序列右边的由右向左移动的游标
    high = end

    while low < high:
        # 如果low与high未重合，high指向的元素不比基准元素小，则high向左移动
        while low < high and alist[high] >= mid:
            high -= 1
        # 将high指向的元素放到low的位置上
        alist[low] = alist[high]

        # 如果low与high未重合，low指向的元素比基准元素小，则low向右移动
        while low < high and alist[low] < mid:
            low += 1
        # 将low指向的元素放到high的位置上
        alist[high] = alist[low]

    # 退出循环后，low与high重合，此时所指位置为基准元素的正确位置
    # 将基准元素放到该位置
    alist[low] = mid

    # 对基准元素左边的子序列进行快速排序
    quick_sort(alist, start, low-1)

    # 对基准元素右边的子序列进行快速排序
    quick_sort(alist, low+1, end)


alist = [54,26,93,17,77,31,44,55,20]
quick_sort(alist,0,len(alist)-1)
print(alist)

复杂度分析

• 最好的时间复杂度为：O(nlogn)

划分函数需要扫描每个元素，每次扫描元素不超过n，时间复杂度为O(n)
在理想的情况下，每次划分将问题分解为两个规模为n/2的子问题，递归求解两个规模的子问题。所需时间为2T(n/2)
合并：因为是原地排序，合并不需要时间复杂度
因此总运行时间为

T(n)=
		O(1) , n=1
		2T(n/2)+O(n) , n>1

最终求解为最好的时间复杂度为O(nlogn)

• 最坏的时间复杂度为: O(n²)

划分函数需要扫描每个元素，每次扫描元素不超过n，时间复杂度为O(n)
在最坏的情况下，每次划分将问题分解后，基准元素的一侧没有元素，其中一侧为规模为n-1的子问题，递归求解该子问题，所需时间为T(n-1)
合并：因为是原地排序，合并不需要时间复杂度
因此总运行时间为

T(n)=
		O(1) , n=1
        T(n-1)+O(n) , n>1

最终求解为最好的时间复杂度为O(n²)