基于C语言的堆排序

Posted 2022-10-29 胖仙人

->Gitee源码点击这里<-
有了向下调整算法和建堆算法的铺垫，我们就可以利用堆来堆数组排序了。
我们之前学过冒泡排序，而堆排序相比冒泡排序效率更高。
堆排序方思路：
a. 若想要将数组排成升序，则需要先将数组建立成大堆（降序则反之，这里以升序为例）
b. 下图是已经建好的一个堆

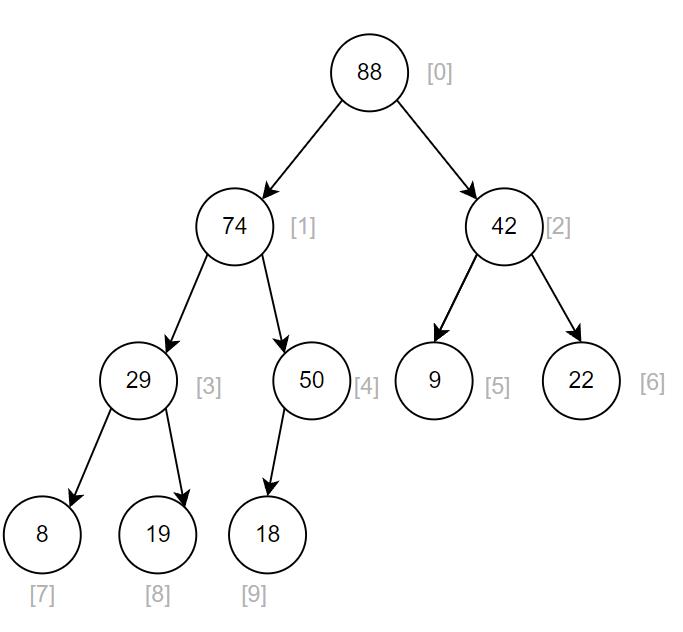
想要将数据排成升序，需要重复如下步骤：
①交换堆顶数据和最后一个数据

②交换过后，"删除"最后一个数据，这里的删除并不是真的删除，而是暂时的不允许访问该空间的值
堆使用数组表示的，访问数组元素需要通过下标，最大的下标值为（数组的长度-1），所以交换过后，我们只需暂时将size(数组长度)-1即可。

③此时剩下的数中，根节点为18，左子树和右子树任然是满足大堆关系，所以堆根节点18向下调整，使剩下的数成为大堆。
循环以上步骤，在此过程中，大的数不断地被排到后面，最终会形成升序排列

代码实现：
堆排是基于向下调整算法和建堆算法实现的，所以我们把上一篇中写好的代码copy过来

void Swap(int* a, int* b) //交换函数

	int tmp = *a;
	*a = *b;
	*b = tmp;


void AdjustDown(int* a, int pos,int size)

	int parent = pos;
	int node = parent * 2 + 1;   //先默认左节点是两个结点中较大的一个
	while (parent * 2 + 1 < size) //调整过程是一个循环,当找到最后一层，即父节点已经没有子节点的时候，则说明调整完成
	
		if (a[node] < a[node + 1] && node+1<size) //比较左节点和右节点的大小,同时要注意没有右节点的情况
		
			node = node + 1;   //如果右节点较大，则和parent交换的结点就要变成右节点
		
		if (a[parent] < a[node])  //判断父结点和子节点的大小，如果子节点大，则交换
		
			Swap(&a[parent], &a[node]);//交换
            
			//交换完成后，需要重新定位父节点和子节点
			parent = node;
			node = parent * 2 + 1;
		
		else 
		
			break;   //如果父节点大，则说明已经整个二叉树已经调整完成了
		
	


void CreateHeap(int* a, int size)

	int child = size - 1;   //要找到最后一个子树的父节点，就要先找最后一棵子树的子节点
	int parent = ((child)-1) / 2;  //通过子节点找到父节点
	for (int i = parent; parent >=0 ; parent--)  //循环，将所有子树转换为大堆，当二叉树的根结点也向下调整完毕后，循环停止
	
		AdjustDown(a, parent, size);
	

接着就是排序过程

void HeapSort(int* a, int size)

	CreateHeap(a, size); //第一步建堆
	
	while (size > 0) //第二部排序
	
		Swap(&a[0], &a[size - 1]);
		size = size - 1;
		AdjustDown(a, 0, size);
	

测试：

int main()

	int a[10] =  18,29,42,8,50,9,22,88,19,74 ;
	int size = sizeof(a) / sizeof(a[0]);
	HeapSort(a, size);
	for (int i = 0; i < size; i++)
	
		printf("%d ", a[i]);
	
	return 0;