四旋翼飞控里 为啥一定要用四元数?用欧拉角不一样吗? 就算用四元数也是将四元数转化为欧拉角进
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了四旋翼飞控里 为啥一定要用四元数?用欧拉角不一样吗? 就算用四元数也是将四元数转化为欧拉角进相关的知识,希望对你有一定的参考价值。
四旋翼飞控里 为什么一定要用四元数?用欧拉角不一样吗? 就算用四元数也是将四元数转化为欧拉角进行调节的,意义何在?
四元数多是用在中间环节,在最终的PID输出的时还是用的欧拉角。我认为造成这个现象的根本原因是抄袭!!对,就是抄袭。
通过6轴或者9轴融合姿态角的算法有两种,这两种我记得没错的话是英国人开发的(国籍可能记错了),并开源了,国内的那些没有研发能力的团体和个人就是用的这个算法,而那个算法的中间环节均为四元数,输出是欧拉角。
我也是没有研发能力的个人,所以也不能透彻理解这个转换的意义,猜测可能是像拉式变换或者傅立叶一样,通过一种域的变换使计算过程简便,也就是三维的'复数域',再可能是通过四元数防止计算过程中出现超过欧拉角表示范围的问题。四元数在旋转合成方面会方便一些,计算量也少于欧拉角,但是!姿态算法里根本没有四元数的旋转合成。
国内的开源的四轴代码都是这样,还有以前看的一个开源代码开始还是开源的,后来还有限制了,就那破代码,也就开发者自己还觉得不错了。
这些代码没有核心的姿态算法的开发能力,就在传感器的数据上'下功夫',就是被玩坏的滤波器,MWC用的滑动均值滤波、互补滤波简单明了,可靠有效,但是我们的开发者不这么认为,不用上椭圆滤波器,多阶低通滤波器,卡尔曼滤波这些复杂的算法就是低端的体现,浮点运算随心情写,也不管用不用的上,能用浮点绝不定点,这都还好,反正他们用的芯片完成他们的代码就是用大炮打蚊子,有的是资源没用,双精度都算的过来。
其中我最受不了的就是他们的卡尔曼滤波了,那个叫卡尔曼?天启者 卡尔玛吧。那都什么算法啊,有什么用,定义个QR就开始计算了,几个矩阵就高大上了,完全的低通性能,就是抑制dv/dt,确实给信号的波动减少了同时也把传感器的中高频信号给过滤掉了,这个可以,问题是中高频都滤掉了,控制频率给提到400+hz是什么意思,信号带宽给限制到了100hz,再把控制频率给升高,有什么用?有什么用?
说的这些都是我能看到源码的算法,当然有很多没有公开源码的好的算法,国内的牛人很多很多,只是他们专注于卖套件,谁都想把自己的劳动有回报,也不会公开,就是这个情况。
开源的国内代码就是这个质量,别想有什么突破,心态就是这样,别想短时间内有突破。
废话说了一堆也没解决你疑惑,实在抱歉。 参考技术A 楼上的朋友说了很多,但基本没怎么回答lz的问题…其实答案很简单,首先欧拉角比较直观更适合人类想象或观察,但四元数更适合机器运算;其次四元数非常适合插值,这是因为他是4维向量;最后四元数可以避免万向节锁死问题。总结就是四元数的计算占用资源较少,可以更方便的对数据进行操作并可以避免一些欧拉角的缺点。 参考技术B 欧拉角是你觉得好用,但机器不觉得啊。需要考虑怎么样计算机器的负载最小
Unity编程四元数(Quaternion)与欧拉角
欧拉旋转、四元数、矩阵旋转之间的差异
除了欧拉旋转以外,还有两种表示旋转的方式:矩阵旋转和四元数旋转。接下来我们比较它们的优缺点。
欧拉角
- 优点:三个角度组成,直观,容易理解。
- 优点:可以进行从一个方向到另一个方向旋转大于180度的角度。
- 弱点:死锁问题。 前面《【Unity编程】欧拉角与万向节死锁(图文版)》已经介绍过万向节死锁问题。
四元数
内部由四个数字(在Unity中称为x,y,z和w)组成,然而这些数字不表示角度或轴,并且通常不需要直接访问它们。除非你特别有兴趣深入了解四元数学,你只需要知道四元数表示三维空间中的旋转,你通常不需要知道或修改x,y和z属性。
- 优点:四元旋转不存在万向节锁问题。
- 优点:存储空间小,计算效率高。
- 弱点:单个四元数不能表示在任何方向上超过180度的旋转。
- 弱点:四元数的数字表示不直观。
矩阵旋转
- 优点:与四元数一样,不存在万向节锁问题
- 优点:可以表示围绕任意轴的旋转,四元数的旋转轴均为通过物体中心点的轴,矩阵则不受限
- 缺点:矩阵旋转使用4x4矩阵,记录16个数值,而四元数只需要4个数值。计算复杂,效率低。
由于Unity中的旋转使用四元数,因此本文重点就放在四元数数学上。矩阵还是某些场合需要用到,比如坐标变换。不过你几乎不需要手动去执行矩阵计算,除非你在做Shader编程,或者是某些需要极端提高效率的场合。后续我计划写一篇文章专门介绍矩阵变换。
四元数的数学
由于前面两篇文章均尽可能采用无数字计算的方式,为的是方便理解。而这里由于需要理解四元数的计算,我们还是需要理解一些复数和欧拉旋转计算方面的基本数学。
复数
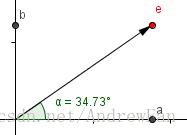
首先了解一下复数,上图中,左右方向的轴(X轴)称为实数轴,上下的轴(Y轴)称为虚数轴。
任意一个二维矢量,都可以使用一个复数形式进行表示。也就是:e = a + bi
其中a是实数,i是虚数,i * i=-1。
至于什么是虚数,我的理解它就是个不同维度的后缀标记和符号而已。i标记了实数轴和虚数轴之间的差异,也就是旋转90度旋转的差别,乘以i意味着这种旋转关系。
为什么i * i=-1?也就是两个虚数i乘积又变成了实数-1?因为从实数轴(1表示)围绕上图中逆时针90度(1*i)到达虚数轴(=i),再逆时针旋转90(1 * i * i)就到达了负实数轴方向(=-1)。所以这里规定i * i=-1。
复数运算
- 加法: (a+bi)+(c+di)=(a+c)+(b+d)i
- 减法: (a+bi)-(c+di)=(a-c)+(b-d)i
- 乘法: (a+bi)(c+di)=ac+bci+adi+bdi^{2}=(ac-bd)+(bc+ad)i
更多复数相关知识,请参考“维基百科-复数_(数学)”
欧拉旋转定理
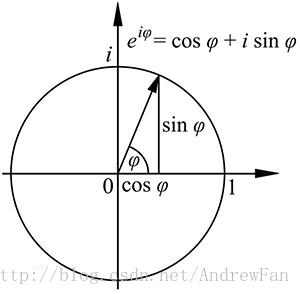
为了方便讨论旋转,我们避开矢量长度的影响,也就是假设问题是基于长度为1的矢量去讨论。由上图可以看出,当长度为1时,矢量落在长度为1的圆形上,此时实数轴上的a = cos(φ),虚数轴上的b = sin(φ),其中φ为旋转角度。
此时的表示形式为 e = cos(φ) + sin(φ)i
那么,使用这样一种形式到底有什么意义呢?数学从来都是工具,如果没有用处,它也就不会存在了。我们接下来看它的作用。
当圆上的一个矢量进行了连续的旋转时时,假设先旋转φ,再旋转θ,则结果应该是两个旋转的角的和的复数形式,即 e = cos(φ+θ)+sin(φ+θ)i
假设:
e1= cos(φ) + sin(φ)i (表示旋转了φ角度)
e2= cos(θ) + sin(θ)i (表示旋转了θ角度)
那么e和e1、e2之间的关系是怎样的?
根据和差公式可以得知
cos(φ+θ)+sin(φ+θ)i
= (cos(φ)cos(θ)-sin(φ)sin(θ))+(sin(θ)cos(φ)+cos(θ)sin(φ))i
= cos(φ)cos(θ)+cos(φ)sin(θ)i+cos(θ)sin(φ)i- sin(φ)sin(θ)
= (cos(φ) + sin(φ)i)*(cos(θ) + sin(θ)i)
= e1 * e2
=>
e = e1*e2
也就是说,连续的旋转(例如这里旋转φ再旋转θ),可以使用两个复数的乘积进行表示。在计算机运算中:
- 如果知道φ=30度,那么计算此单位矢量再旋转θ=40度是很容易的,只需要直接运算cos(φ+θ)和sin(φ+θ)即可。
- 如果知道一个矢量(a+bi),不知其φ值,要对其进行旋转θ=40度,那么也就有了快速的计算方法,即:
(a+bi) * (cos(40)+sin(40)i) = (a * cos(40)-b * sin(40)) + (b * cos(40) + a * sin(40))i
结果:二维向量 x = a * cos(40)-b * sin(40),y= b * cos(40) + a * sin(40)
可以快速计算出二维矢量结果,而不必先求φ。
因此这就是复数和欧拉旋转定理的作用,它可以使用复数很方便地表示出二维矢量的旋转变化。
四元数
相对于复数为二维空间,为了解决三维空间的旋转变化问题,爱尔兰数学家威廉·卢云·哈密顿把复数进行了推广,也就是四元数。
以下均为定义,所谓定义,就是我们人为设置的概念和计算方法,它们本身或许没有什么意义,但是如果按照这些概念和方法计算出某些有意义的结果,那么这些定义也就有了相应的意义。
四元数定义
四元数定义i、j、k三个虚数单位参与运算,并有以下运算规则:
以上是关于四旋翼飞控里 为啥一定要用四元数?用欧拉角不一样吗? 就算用四元数也是将四元数转化为欧拉角进的主要内容,如果未能解决你的问题,请参考以下文章