应用统计学总体均值的假设检验

Posted 2023-02-18 古月书斋

一、假设检验的基本原理

“小概率原理”，是指概率很小的事件在次试验中通常是不可能出现的。若在原假设成立的前提下，通过一次抽样就使小概率事件得以发生，可以认为原假设是不正确的，应予以否定;反之，则不能否定原假设。这就是假设检验判断的基本逻辑。在假设检验的应用中，通常以显著性水平α(o<α<1)作为小概率的界限。一般地，α取0.05 (5%) 。

二、检验类型

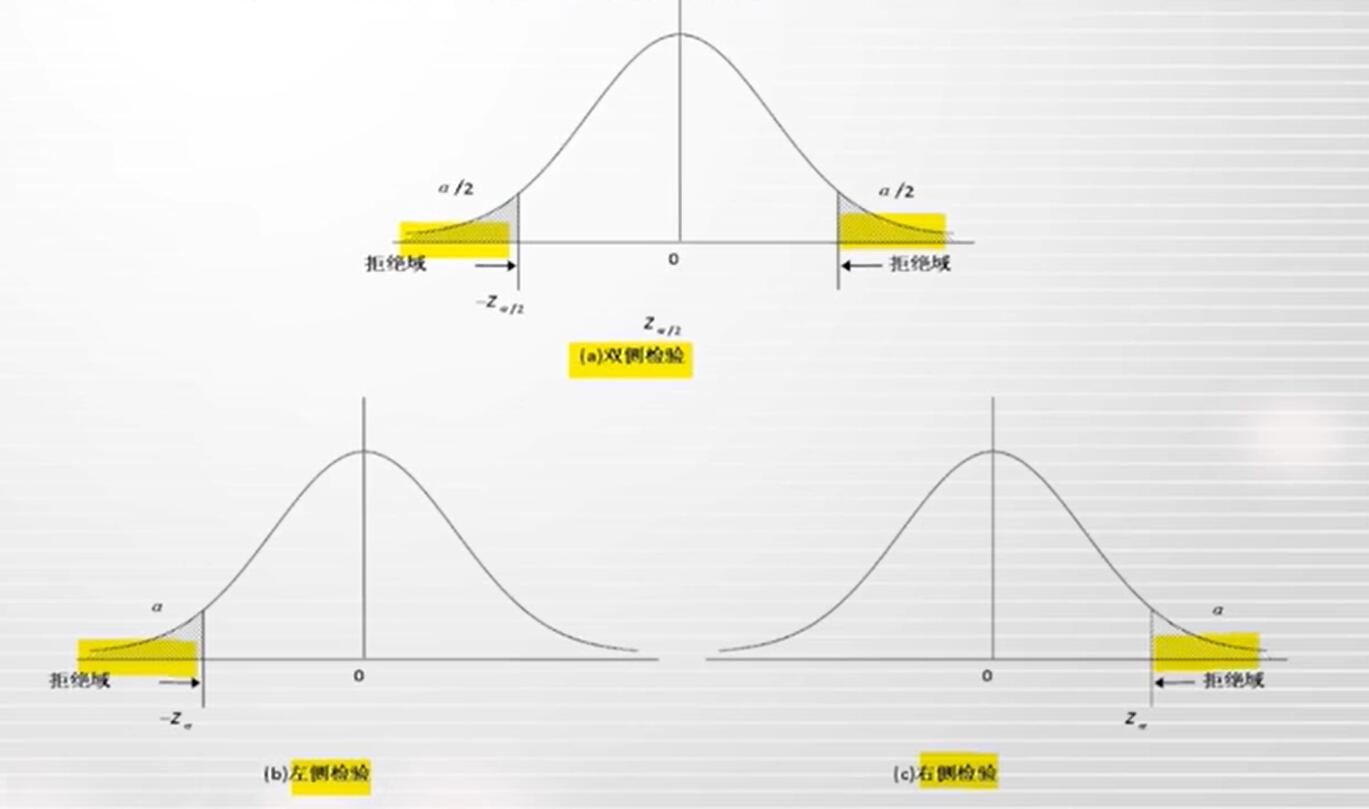
 双侧检验用于检验两个检测值是否相对；左侧检验则用于小于等于的检验；右侧检验则用于小于等于的检验。

三、两类错误

1．第一类错误（弃真错误），指错误的拒绝了真实的原假设。显著性水平α是犯第一类错误的概率。
2．第二类错误（纳伪错误），指错误的接受了错误的原假设。犯第二类错误大小的概率用β表示。

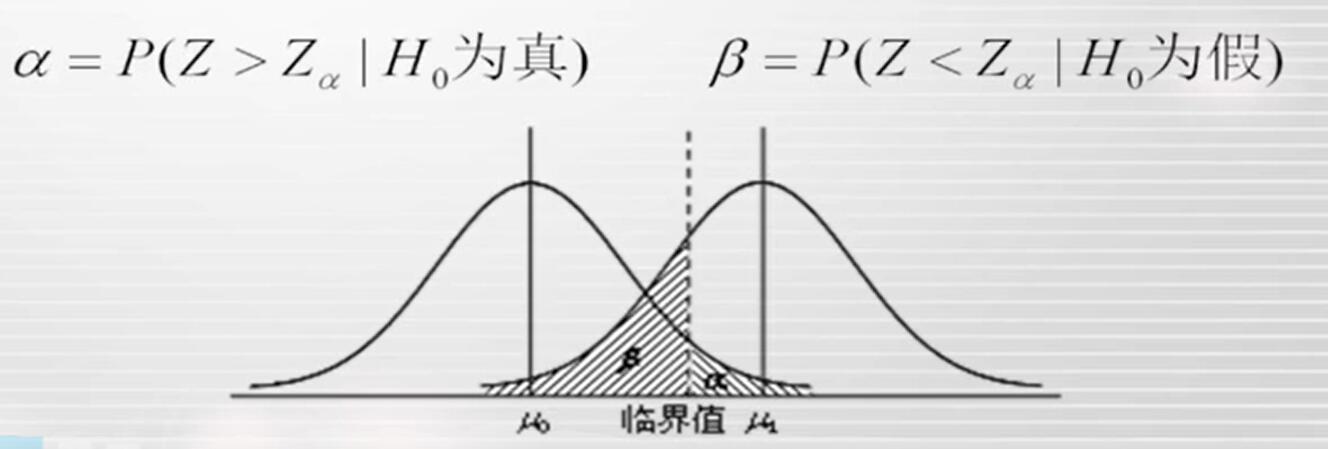
由于β表示为接受不真实原假设结论的概率，那么1-β就指拒绝不真实原假设的概率。若1-β的数值越接近于1，表明不真实的原假设几乎都能够被拒绝。反之，若1-β接近于0，表明犯第二类错误的可能性很大。因此，1-β可以用来表示假设检验工作好坏的一个指标，称之为检验功效。在α给定的条件下，1-β越大，检验的功效越好。

四、总体均值的假设检验

（一）、总体标准差已知

和区间估计类似，如果总体标准差已知，对于总体服从正态分布或者总体分布状况未知,但样本容量n充分大（n>=30）的情况，我们也可以构造服从标准正态分布的检验统计量Z来进行假设检验:

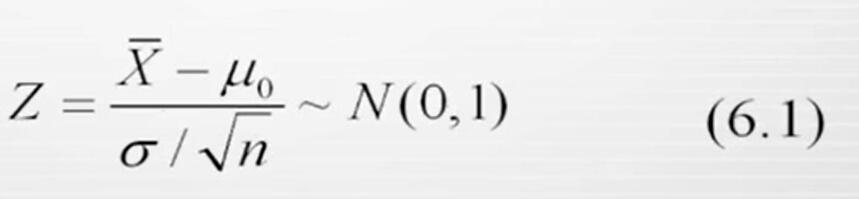
 例6-1 某调查公司想了解城市居民户每天看电视的平均时间，以了解人们看电视的平均时间是否与10年前一样。根据报道，10年前每户家庭看电视时间的总体均值为7.5小时/天。该调查公司随机选择了200户家庭户进行调查，样本数据显示，目前每户家庭看电视的平均时间为6.7小时/天。已知每天每户看电视时间的总体标准差为2.5小时，试问在显著水平下，城市居民户每天观看电视时间与10年前是否有显著差异?

 （二）、总体标准差未知

和区间估计类似，如果总体标准差未知，对于总体服从正态分布或者总体分布状况未知,但样本容量n充分大（n>=30）的情况，我们也可以构造服从自由度为n-1的t分布的检验统计量t来进行假设检验:

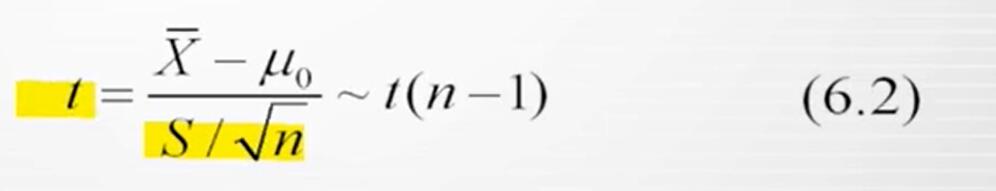
在大样本下，t分布与标准正态分布近似，此时可以用Z统计量代替t统计量。

【例6-2】

某糖果生产基地，生产的标准是每袋糖果的净重为500(克)。今从一批产品中抽出10袋，实际测得每袋糖果的净重（克）为:512，503，498，507，496，489，499，501，496，506给定显著性水平，假定糖果的净重服从正态分布，试问该批产品的重量是否显著地高于标准？

【例6-15】(单总体均值检验)某城镇去年居民家庭平均每人每月生活费收入275元。根据抽样调查,得到今年该城镇50户居民家庭平均每人每月生活费收入数据。试问该城镇居民家庭平均每人每月生活费收入今年与去年比较是否明显提高（α=0.05) ?

 临近值=T.INV.2T(0.05,COUNT(X)-1)

五、两个总体均值之差的检验

（一）、独立样本的均值检验

1、总体标准差已知

当总体服从正态分布时，根据正态分布再生定理，样本平均数服从正态分布。当总体不服从正态分布时,根据中心极限定理，当n充分大时(通常要求n≥30），样本平均数近似服从正态分布。

和两个总体均值之差的区间估计类似：

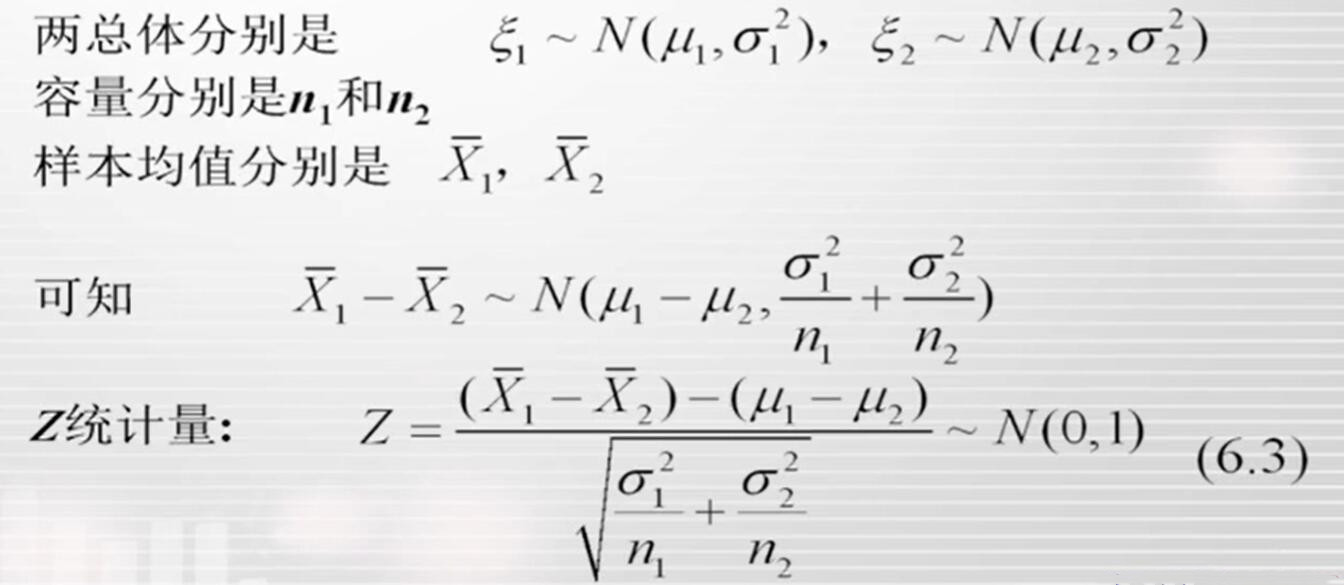
 例6-3

为了研究商学院学生和工学院学生在毕业之后平均收入的高低，从某学校中抽查了30名商学院毕业生和24名工学院毕业生，测得收入的平均值分别为2100元和1800元，假定两学院毕业生的薪金均服从正态分布，且已知总体标准差分别为250元和300元;试问抽样结果是否支持“商学院学生比工学院学生工薪较高”的这一观点( α=0.05）?

 

2、总体标准差未知，但相等

 例6-4

某公司研究两家原材料供应商的送货时间，越短的平均送货时间将获得较高的满意度。目前来看，该公司对供应商A基本满意，如果其平均送货时间等于或小于供应商B，则公司将继续与供应商A合作;否则公司将从供应商B购买材料。现分别从供应商A和供应商B处订购23份和19份的产品，从送货时间来看，供应商A的平均送货时间为12.5天/份，标准差为3天;供应商B的平均送货时间为14天/份，标准差为2天。现假定供应商A与供应商B送货时间的总体标准差相同，试问，在5%的显著水平下，供应商A的送货时间是否显著比供应商B更少?公司应如何选择?

 

【例6-16】(两独立样本均值检验，等方差）某商店销售的商品来自甲、乙两家厂商，为了考察商品性能的差异，从甲、乙两家厂商的产品中分别抽取了8件和9件，测定其性能指标，得到如下数据:
甲厂产品X:0.30，0.12，018，0.25，0.27，0.08，0.190，13;
乙厂产品Y: 0.28，0.30，0.11，0.14，0.35，0.26，0.14，0.31，0.20。
根据以往的经验，两厂商产品的性能指标服从相同方差的正态分布。问在显著性水平0.1下，两家产品的性能是否存在明显的差异。 

解答：

选择t-检验双样本等方差假设

 

 

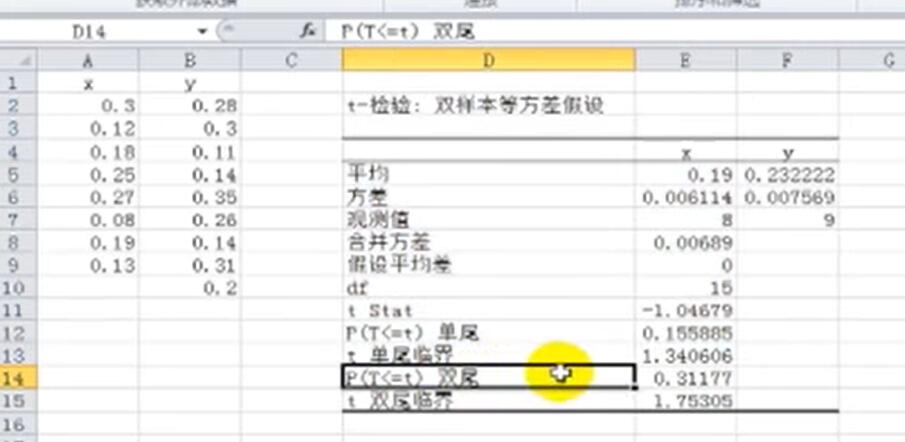
P双尾值为0.3177，大于显著性水平0.1 。因此，我们不能拒绝原假设。

 

六、配对样本的均值检验

 例6-5

某厂商生产两种型号洗衣机，一款为豪华型，一款为经济型。厂商在4周内分别从同时销售两款洗衣机的7个零售商那里获取销售资料，以了解两种型号洗衣机的市场受欢迎度是否相同。数据记录如下（单位:千元）:

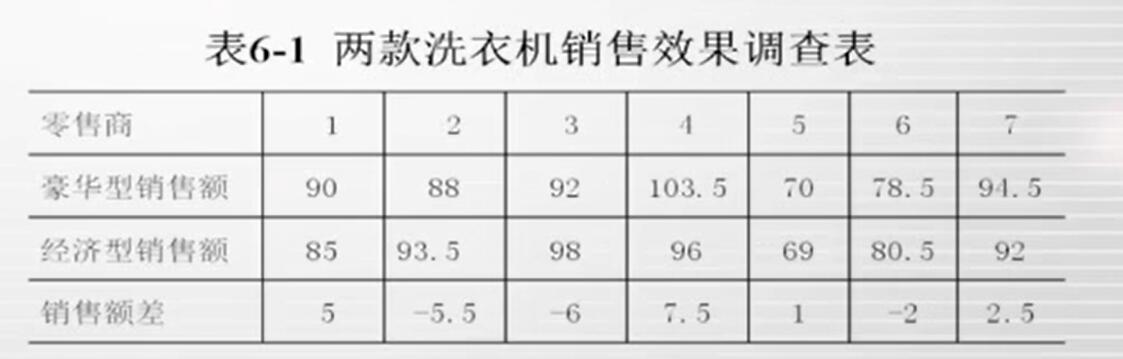
 试在显著性水平0.05下，检验调查结果是否支持“厂家认为两款洗衣机有相同市场欢迎度“的观点。

 

  七、总体成数的假设检验

 例6-6 某企业声明有30%以上的消费者对其产品质量满意。如果随机调查600名消费者，表示对该企业产品满意的有220人。试在显著性水平0.05下，检验调查结果是否支持企业的自我声明。

 

  八、P值的计算