网格擦除效果——类似宝剑大师

Posted 2022-10-18 CZandQZ

最近找工作有时间可以把之前工作中遇到的一些问题及解决办法写出来，当然这份代码并不是公司的那份代码，这份代码是在源项目上解决思路写出来的，所以做出来可能有点乱。首先思路跟2D的思路差不多的，因为我们只是在做3D表现而已。首先在擦除的时候他的原理跟2D的一样，但是他的网格渲染方式可能跟2D就不一样了，还是一样我们需要首先生成一个3D的网格。

3D网格生成的核心代码如下：

private GameObject GeneratorBody(string bodyName, Polygon points)
    
        GameObject obj = new GameObject(bodyName);
        obj.transform.position = Vector3.zero;

        Mesh mesh = new Mesh();
        obj.AddComponent<MeshRenderer>().material = _bodyMaterial;
        var mf = obj.AddComponent<MeshFilter>();

        List<Vector3> verticles = new List<Vector3>();
        List<Vector3> middle = new List<Vector3>();
        for (int i = 0; i < points.Count; i++)
        
            Vector3 p1 = new Vector3(points[i].X / FloatScale, points[i].Y / FloatScale, 0f);
            verticles.Add(p1);
            middle.Add(p1 + new Vector3(0, 0, Width / 2f));
        

        mf.mesh = Recalc(false, verticles, verticles, middle, obj.transform);
        obj.AddComponent<MeshCollider>().sharedMesh = mesh;

        return obj;
    

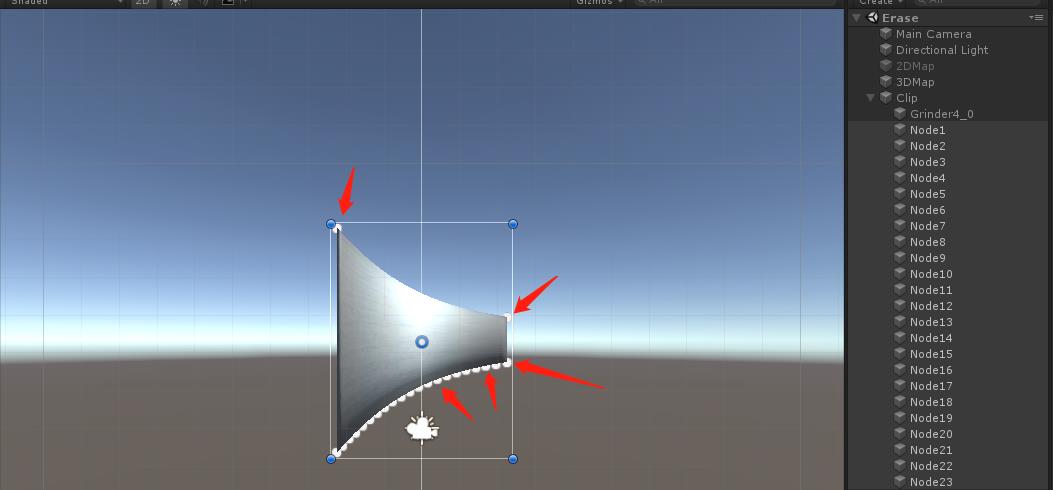
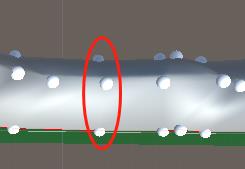
所有的顶点信息都记录在verticles内，但是看这里有一个middle数组，这个数组的意义是什么呢？我们截图看一下整个初始网格的信息。

红色箭头标的就是我们 middle，所以这里就很好解释了middle.Add(p1 + new Vector3(0, 0, Width / 2f));

这里渲染的逻辑是前后2个面是一起渲染的，中间的一个环又是单独渲染的。为啥中间那个环一个要分为4个三角面的呢，其实这里2个三角面就完全够了么，这里岂不是多此一举？并不是的，这样写的逻辑是因为最后一个磨刀锋的环节需要，Recalc方法就是主要计算前后2个面和周围边的渲染了。

1 首先说一下第一步就是擦除

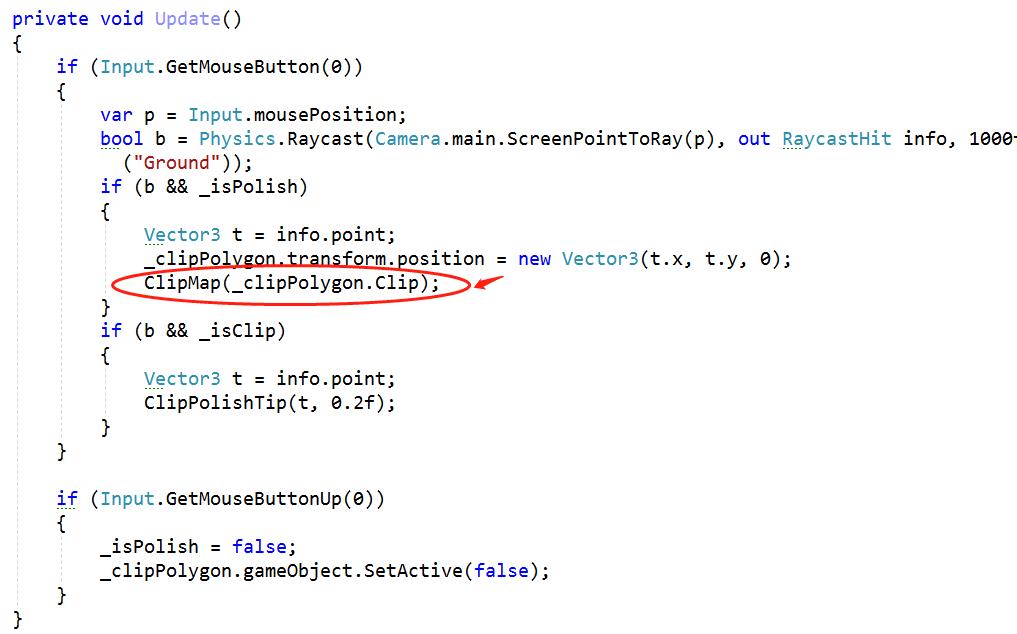
 ClipMap方法中传进去的参数是就是一个包含一些顶点信息的数组。数组的顶点

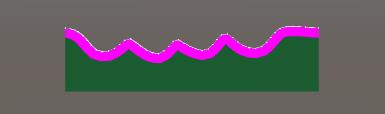
 数组的顶点根据当前模型组成一个包围点，而这些包围点可以理解为集合B，初始生成的模型顶点组成集合A，所以这里还是A-B就是剩下的集合点。下面就是我们擦除的效果图如下：

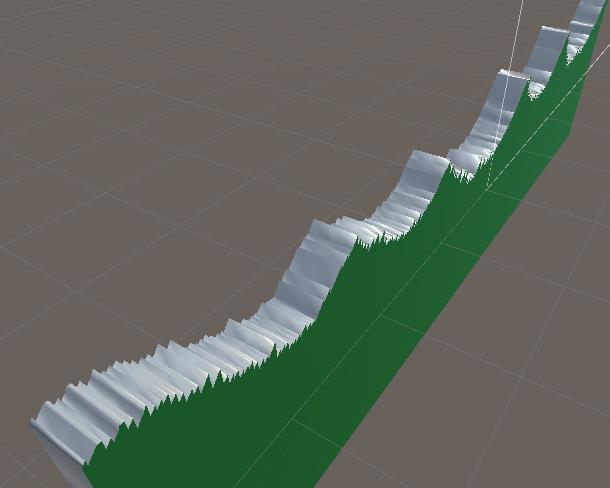
 很明显出现了很严重的锯齿的，导致这种情况一种是玩家的操作，一种是擦除的模型包围顶点不够圆滑。所以这里我们需要一种拟合曲线来完成，什么叫拟合曲线呢？，看个图就了解了，至于怎么求，可以在维基百科上找贝尔赛线拟合。这个贝塞尔曲线拟合算法我也是在老外的网站上找到的。我这里下载的是dll文件

 

 拟合的就是根据一些点找到一条曲线，然后让曲线大概能描述点的分布情况。我们看一下拟合后的顶点的分布。

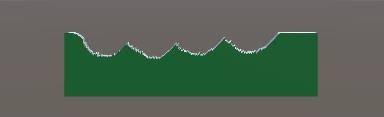
 图形上的一些白色的球 就是我们拟合之后的顶点信息，拟合之前首先求得所有贝塞尔拟合关键贝塞尔顶点信息，

 CurvePreprocess.Linearize函数的意义是根据误差为0.1，在list所有数组中补点，打个比方加入a点和b点之前相差0.3,那么我们需要在a和b之间补足a1，a2。a1距离a为0.1，a2距离a为0.2，说的直白一点就是判断路径上所有点 判断他们之间的距离如果大于0.1就在两者之间补点，反之就将原先的点补充进来。具体不懂可以查阅该dll的源代码。

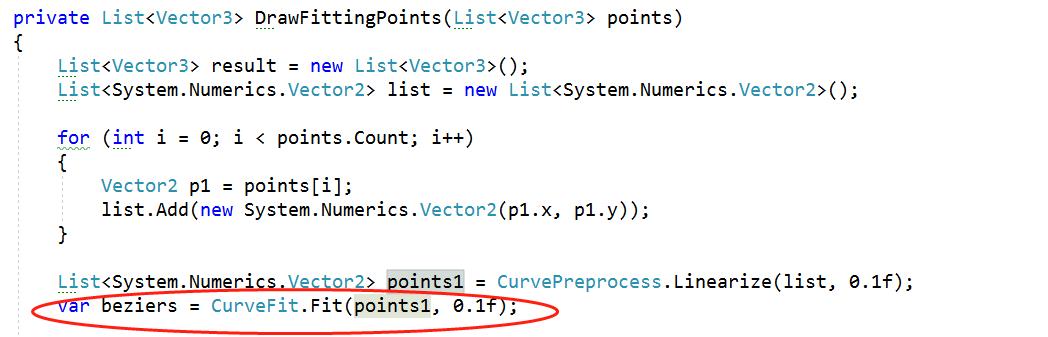
CurveFit.Fit函数第一个参数是顶点信息，第二个参数意义是最大误差，误差越大 那么拟合的曲线也可能偏差越大，误差越小那么拟合的曲线可能越接近，这个很好理解。拟合曲线求解出来之后就是根据曲线采样顶点了。就是这样一段曲线我们需要采多少个顶点

private List<Vector3> DrawFittingPoints(List<Vector3> points)
    
        List<Vector3> result = new List<Vector3>();
        List<System.Numerics.Vector2> list = new List<System.Numerics.Vector2>();

        for (int i = 0; i < points.Count; i++)
        
            Vector2 p1 = points[i];
            list.Add(new System.Numerics.Vector2(p1.x, p1.y));
        

        List<System.Numerics.Vector2> points1 = CurvePreprocess.Linearize(list, 0.1f);
        var beziers = CurveFit.Fit(points1, 0.1f);

        Gizmos.color = Color.red;

        Spline spline = new Spline(10);
        for (int i = 0; i < beziers.Length; i++)
        
            spline.Add(beziers[i]);
        

        int num = (int)Math.Round(spline.Length * 5f);
        float num2 = 1f / (float)(num - 1);
        for (int i = 0; i < num; i++)
        
            float u = (float)i * num2;
            Spline.SamplePos samplePosition = spline.GetSamplePosition(u);
            System.Numerics.Vector2 p = spline.Curves[samplePosition.Index].Sample(samplePosition.Time);

            Vector3 p1 = new Vector3(p.X, p.Y, 0);
            result.Add(p1);
        

        return result;
    

2 第一步擦除之后就到了打磨了，打磨的过程就是把刀锋网格生成的过程了，首先得知道那些是刀锋上的顶点，那些刀背上的顶点的，具体看一下图来讲解一下

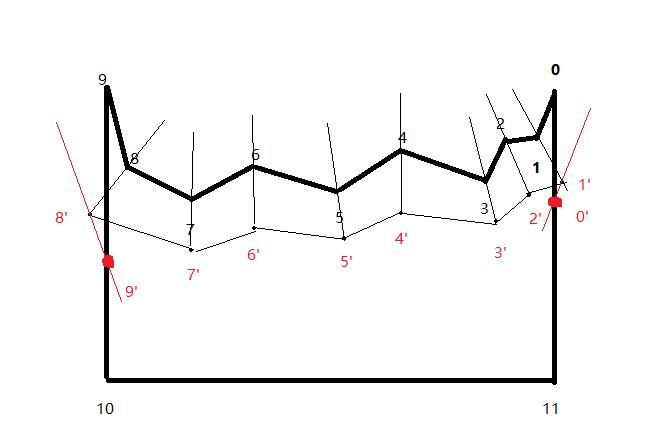
 从图中我们可以看出0-9号顶点是刀锋，首先1到8号点 是通过角平分线求得1’-8’点，讲述一下1’顶点求得原则。首先2号点-1号点定义向量A，0号点-1号点定义向量B，A，B向量的夹角Angle，夹角小于180度，但是其实A向量需要旋转的角度其实是（360-Angle）/2,但是像6号节点他所旋转的角度就是Angle/2,所以根据A，B向量进行Cross求得一个垂直向量，如果这个垂直向量和当前图形组成的面的垂直向量一致的话 那么就是Angle/2，反之就是（360-Angle）/2，所以代码就是

float width = 0.3f;
for (int i = 1; i < list.Count - 1; i++)

    Vector2 p1 = list[i - 1] - list[i];
    Vector2 p2 = list[i + 1] - list[i];
    float angle = Vector3.Angle(p1, p2);
    Vector3 normal = Vector3.Cross(p1, p2);
    float value = Vector3.Dot(normal, Vector3.back);
    if (value < 0)
    
        angle = 360 - angle;
    

     Vector3 p3 = Quaternion.AngleAxis(angle / 2f, Vector3.back) * p1;
     Vector3 targetPos = p3.normalized * width + list[i];
     results.Add(targetPos);

这个时候9’号点和0’号点的求法是 首先0’点是以1’点为中心0号点-1号点为方向组成的直线和0-11号点组成的线段求得交点，同理9’点的求法类似。

int index = list.Count - 1;
        Vector3 t1 = GetLine2Line(results[0], list[1] - list[0], list[0], check1 - list[0]);
        Vector3 t2 = GetLine2Line(results[results.Count - 1], list[index] - list[index - 1], list[index], check2 - list[index]);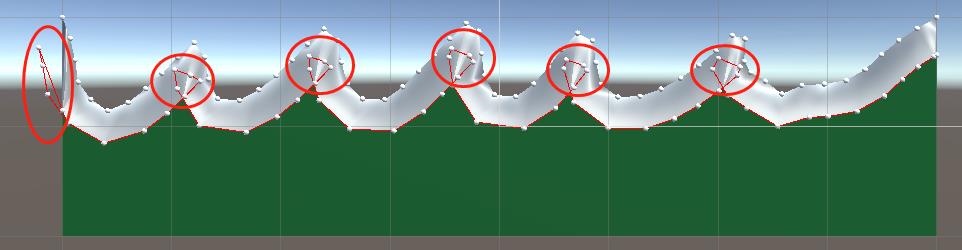

 上图就是通过上面代码的计算后就是得到了一些点，但是出现了一个环，这些环我们是需要去掉的，同时在在多边形外的顶点也是我们需要去掉的。

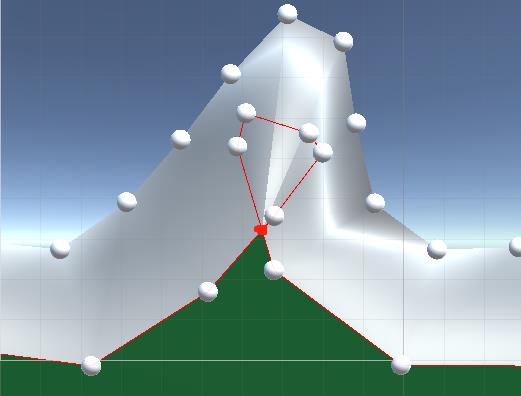
 我们如何去掉环同时加上红色的顶点呢，这里的做法首先把环上所有的顶点都赋值为红色的顶点，然后再移除相同的顶点。下面是将环上的顶点变为红色的顶点。

private void RecalculatePathCross(List<Vector3> pathList)
    
        for (int i = 0; i < pathList.Count - 1; i++)
        
            Vector3 p1 = pathList[i];
            Vector3 p2 = pathList[i + 1];
            Segment2 check = new Segment2(new Vector2(p1.x, p1.y), new Vector2(p2.x, p2.y));

            for (int j = i + 2; j < pathList.Count - 1; j++)
            
                Vector3 p3 = pathList[j];
                Vector3 p4 = pathList[j + 1];
                Segment2 t1 = new Segment2(new Vector2(p3.x, p3.y), new Vector2(p4.x, p4.y));
                Segment2Segment2Intr intr;
                bool b = Intersection.FindSegment2Segment2(ref check, ref t1, out intr);
                if (b)
                
                    for (int k = i + 1; k <= j; k++)
                    
                        pathList[k] = new Vector3(intr.Point0.x, intr.Point0.y, 0);
                    
                    i = j;
                
            
        
    

原理是很简单，一种暴力求解，第一趟循环判断0-1线段和2-3,3-4....等等，如果有相交的话就将环中的顶点全部赋值为交点。同时把j赋值给i，减少循环的次数。第二次循环就从1-2线段和3-4,4-5...等等。同时把在多边形外的顶点去掉。

private List<Vector3> ModifyOutPolygonPoint(List<Vector3> originList)
    
        List<Vector3> results = new List<Vector3>();

        Vector3 c1 = originList[0];
        Vector3 c2 = originList[originList.Count - 1];

        for (int i = 0; i < originList.Count; i++)
        
            Vector3 c3 = originList[i];
            if (c3.x > c1.x)
            
                results.Add(c1);
                continue;
            
            if (c3.x < c2.x)
            
                results.Add(c2);
                continue;
            
            results.Add(c3);
        

        return results;

    

去掉相同的节点。然后就可以渲染出上图绿色的部分了，应为需要用到Triangulate.Points这个api，所以不能存在相同的节点（位置一样的节点）。但是我们渲染刀锋得时候如果上面的节点和下面的节点个数不一致，就没法重新组织三角面，因为你根本就无法判断那几个点组成一个三角面，所以在绘制刀锋得时候我们不需要去掉相同的节点。

图中我们可以看到3个点，最高的那个点即中间那个点就是通过拟合之后所求得点， 而前面那个点就是通过角平分然后去掉环，去掉不在多边形内（顶点的x坐标>最右边顶点X坐标和顶点的x坐标<最左边顶点X坐标）等操作后求得点，而最后面那个顶点是在最前面顶点+new Vector3(0, 0, Width)，因为需要保持中间顶点数组和前后顶点数组数量保持一致，所以这里不能剔除一些相同的节点，应为那样不方便绘制。至于刀锋顶点数组的判断其实很好理解，定义求得最右边且y大于最小Y值即（-height / 2f）的顶点索引f，定义求得最左边且y大于最小Y值即（-height / 2f）的顶点索引l。然后一次循环即可求得所有顶点。至于刀锋顶点索引关系这些可能需要一点3D空间想象能力了，这里用一张图来帮助理解这整个的索引关系。

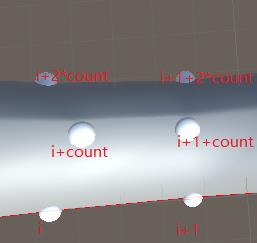
 首先有一个前提就是刀锋所有的顶点都是顺时针添加的，Unity用的左手定则，count等于一圈的顶点，前=中=后。以图中所组成的6个点所组成的所以顶点的绘制顺序为

 triangles.Add(i + 1 + count); triangles.Add(i);  triangles.Add(i + count);
 triangles.Add(i + 1); triangles.Add(i);  triangles.Add(i + 1 + count);

 triangles.Add(i + 1 + 2 * count); triangles.Add(i + count);  triangles.Add(i + 2 * count);
 triangles.Add(i + 1 + count); triangles.Add(i + count);  triangles.Add(i + 1 + 2 * count);

同时最后一个点的下一个点是第一个点，所以最后一个点的绘制得单独拿出来绘制，所以它的绘制顺序为

 triangles.Add(count); triangles.Add(count - 1); triangles.Add(2 * count - 1);
 triangles.Add(0); triangles.Add(count - 1); triangles.Add(count);

triangles.Add(2 * count); triangles.Add(2 * count - 1); triangles.Add(3 * count - 1);
triangles.Add(count); triangles.Add(2 * count - 1); triangles.Add(2 * count);

基本上所有的原理及实现思路都介绍完了，最后贴出项目的源码了

链接: https://pan.baidu.com/s/1O93qGqfzDYrSIUNdjOEQVQ 提取码: x5uj 如果有不是很明白的可以加本人的qq：1850761495