求高手帮忙sql写法:树节点放一个表中,怎么用一条语句查询一个节点及对应的所有父节点信息。
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了求高手帮忙sql写法:树节点放一个表中,怎么用一条语句查询一个节点及对应的所有父节点信息。相关的知识,希望对你有一定的参考价值。
表结构和jyl_19给出的就可。我要的是一个子节点对应的父节点信息和它显示在一行里。
类似于:select * from table1 t1 left outer join table1 t2 on t1.pid=t2.id left ......知道t2.pid=0结束。这样的结果。我想用存储过程,但不知道在存储过程里怎么执行一个存放语句的varchar变量并把结果给另一个变量。如:@sql varchar(5000),@co int;set @co=--执行@sql的结果。
oracl语法示例如下、
CREATE TABLE TBL_TEST
(
ID NUMBER, --主键
NAME VARCHAR2(100 BYTE),
PID NUMBER DEFAULT 0 --------父节点主键
);
插入测试数据:
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('1','10','0');
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('2','11','1');
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('3','20','0');
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('4','12','1');
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('5','121','2');
从Root往树末梢递归
select * from TBL_TEST
start with id=1
connect by prior id = pid
从末梢往树ROOT递归
select * from TBL_TEST
start with id=5
connect by prior pid = id
SQL server 2005语法示例如下、
CREATE TABLE TBL_TEST
(
ID int,
NAME VARCHAR(100),
PID int DEFAULT 0
);
插入测试数据:
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('1','10','0');
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('2','11','1');
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('3','20','0');
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('4','12','1');
INSERT INTO TBL_TEST(ID,NAME,PID) VALUES('5','121','2');
select * from TBL_TEST
-- 从Root往树末梢递归
with cte as
(select *,0 as TLevel from TBL_TEST where ID=1
union all
select t1.*,t2.TLevel+1 from TBL_TEST t1 inner join cte t2 on t1.PID=t2.ID)
select * from cte
-- 从末梢往树ROOT递归
with cte as
(select *,0 as TLevel from TBL_TEST where ID=5
union all
select t1.*,t2.TLevel+1 from TBL_TEST t1 inner join cte t2 on t1.ID=t2.PID)
select * from cte追问
这种方法也可以查出结果集,不过是针对一条生成了列表,我需要的是这些显示为一行,也就是类似left outer join ,把所有父级信息显示在此行的后面! 很感谢~!
追答如果只找一级父节点,可以直接left join
select * from table1 t1 left outer join table1 t2 on t1.pid=t2.id
传参数可以用sp_executesql,实例传回id=2的父节点、
declare @str nvarchar(1000)
declare @co int
set @str='select @i=t2.id from TBL_TEST t1 left outer join TBL_TEST t2 on t1.pid=t2.id where t1.id=2'
exec sp_executesql @str,N'@i int out',@i=@co out
select @co
不是一级,不确定是多少级。
追答适用于sqlserver2005以上环境
with cte as
(select *,ID as Seed from TBL_TEST where ID=5
union all
select t1.*,t2.Seed from TBL_TEST t1 inner join cte t2 on t1.ID=t2.PID)
select parent=cast((select cast(PID as varchar)+',' from cte for xml path('')) as varchar)
Id Pid Name
1 0 A
2 1 B
3 2 C
4 1 D
5 0 E
6 5 F
……
--在SQL中定义一个函数: [GET_CHILD]
CREATE FUNCTION [GET_CHILD]
(
@ID VARCHAR(14)
)
RETURNS @T_LEVEL
TABLE(ID VARCHAR(14),
LEVEL INT)
WITH ENCRYPTION --加密存储过程
AS
BEGIN
DECLARE @LEVEL int
SET @LEVEL = 1
INSERT @t_LEVEL
SELECT @ID
,@LEVEL
WHILE @@ROWCOUNT > 0
BEGIN
SET @LEVEL = @LEVEL + 1
INSERT @T_LEVEL
SELECT A.ID
,@LEVEL
FROM Table A
,@T_LEVEL B
WHERE A.PID = B.ID
AND B.LEVEL = @LEVEL - 1
END
RETURN
--调用该函数得到结果的SQL语句:
SELECT A.*
FROM TB A, GET_CHILD('002') B
WHERE A.ID = B.ID
看看这样是否可以通过一个子节点把它的所有父节点列出来? 参考技术B 你的表结构是什么样子的,是包含 子节点 和父节点两个字段吗?追问
表结构和jyl_19给出的就可。我要的是一个子节点对应的父节点信息和它显示在一行里。
类似于:select * from table1 t1 left outer join table1 t2 on t1.pid=t2.id left ......知道t2.pid=0结束。这样的结果。
完全二叉树的节点个数,你怎么求?
我们从普通二叉树和完全二叉树两个角度来分析!
222.完全二叉树的节点个数
给出一个完全二叉树,求出该树的节点个数。
示例 1:
-
输入:root = [1,2,3,4,5,6] -
输出:6
示例 2:
-
输入:root = [] -
输出:0
示例 3:
-
输入:root = [1] -
输出:1
思路
本篇给出按照普通二叉树的求法以及利用完全二叉树性质的求法。
普通二叉树
首先按照普通二叉树的逻辑来求。
这道题目的递归法和求二叉树的深度写法类似, 而迭代法,遍历模板稍稍修改一下,记录遍历的节点数量就可以了。
递归遍历的顺序依然是后序(左右中)。
递归
如果对求二叉树深度还不熟悉的话,看这篇:。
-
确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回以该节点为根节点二叉树的节点数量,所以返回值为int类型。
代码如下:
int getNodesNum(TreeNode* cur) {
-
确定终止条件:如果为空节点的话,就返回0,表示节点数为0。
代码如下:
if (cur == NULL) return 0;
-
确定单层递归的逻辑:先求它的左子树的节点数量,再求的右子树的节点数量,最后取总和再加一 (加1是因为算上当前中间节点)就是目前节点为根节点的节点数量。
代码如下:
int leftNum = getNodesNum(cur->left); // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum = leftNum + rightNum + 1; // 中
return treeNum;
所以整体C++代码如下:
// 版本一
class Solution {
private:
int getNodesNum(TreeNode* cur) {
if (cur == 0) return 0;
int leftNum = getNodesNum(cur->left); // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum = leftNum + rightNum + 1; // 中
return treeNum;
}
public:
int countNodes(TreeNode* root) {
return getNodesNum(root);
}
};
代码精简之后C++代码如下:
// 版本二
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == NULL) return 0;
return 1 + countNodes(root->left) + countNodes(root->right);
}
};
-
时间复杂度:O(n) -
空间复杂度:O(logn),算上了递归系统栈占用的空间
网上基本都是这个精简的代码版本,其实不建议大家照着这个来写,代码确实精简,但隐藏了一些内容,连遍历的顺序都看不出来,所以初学者建议学习版本一的代码,稳稳的打基础。
迭代法
如果对求二叉树层序遍历还不熟悉的话,看这篇:。
那么只要模板少做改动,加一个变量result,统计节点数量就可以了
class Solution {
public:
int countNodes(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
int result = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
result++; // 记录节点数量
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};
-
时间复杂度:O(n) -
空间复杂度:O(n)
完全二叉树
以上方法都是按照普通二叉树来做的,对于完全二叉树特性不了解的同学可以看这篇 ,这篇详细介绍了各种二叉树的特性。
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
完全二叉树(一)如图: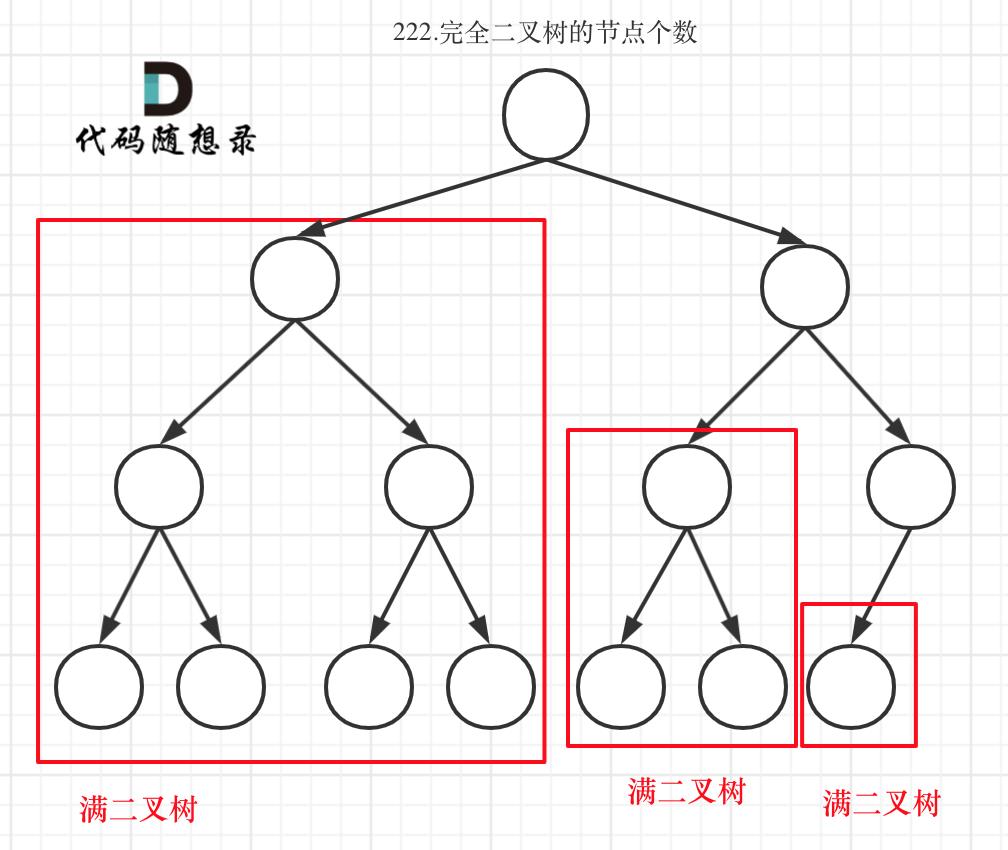
完全二叉树(二)如图:
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
C++代码如下:
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftHeight = 0, rightHeight = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left) { // 求左子树深度
left = left->left;
leftHeight++;
}
while (right) { // 求右子树深度
right = right->right;
rightHeight++;
}
if (leftHeight == rightHeight) {
return (2 << leftHeight) - 1; // 注意(2<<1) 相当于2^2,所以leftHeight初始为0
}
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
-
时间复杂度:O(logn * logn) -
空间复杂度:O(logn)
其他语言版本
Java
class Solution {
// 通用递归解法
public int countNodes(TreeNode root) {
if(root == null) {
return 0;
}
return countNodes(root.left) + countNodes(root.right) + 1;
}
}
class Solution {
/**
* 针对完全二叉树的解法
*
* 满二叉树的结点数为:2^depth - 1
*/
public int countNodes(TreeNode root) {
if(root == null) {
return 0;
}
int leftDepth = getDepth(root.left);
int rightDepth = getDepth(root.right);
if (leftDepth == rightDepth) {// 左子树是满二叉树
// 2^leftDepth其实是 (2^leftDepth - 1) + 1 ,左子树 + 根结点
return (1 << leftDepth) + countNodes(root.right);
} else {// 右子树是满二叉树
return (1 << rightDepth) + countNodes(root.left);
}
}
private int getDepth(TreeNode root) {
int depth = 0;
while (root != null) {
root = root.left;
depth++;
}
return depth;
}
}
Python
递归法:
class Solution:
def countNodes(self, root: TreeNode) -> int:
return self.getNodesNum(root)
def getNodesNum(self, cur):
if not cur:
return 0
leftNum = self.getNodesNum(cur.left) #左
rightNum = self.getNodesNum(cur.right) #右
treeNum = leftNum + rightNum + 1 #中
return treeNum
递归法:精简版
class Solution:
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
return 1 + self.countNodes(root.left) + self.countNodes(root.right)
迭代法:
import collections
class Solution:
def countNodes(self, root: TreeNode) -> int:
queue = collections.deque()
if root:
queue.append(root)
result = 0
while queue:
size = len(queue)
for i in range(size):
node = queue.popleft()
result += 1 #记录节点数量
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result
完全二叉树
class Solution:
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
left = root.left
right = root.right
leftHeight = 0 #这里初始为0是有目的的,为了下面求指数方便
rightHeight = 0
while left: #求左子树深度
left = left.left
leftHeight += 1
while right: #求右子树深度
right = right.right
rightHeight += 1
if leftHeight == rightHeight:
return (2 << leftHeight) - 1 #注意(2<<1) 相当于2^2,所以leftHeight初始为0
return self.countNodes(root.left) + self.countNodes(root.right) + 1
旧文链接:
-------------end------------
以上是关于求高手帮忙sql写法:树节点放一个表中,怎么用一条语句查询一个节点及对应的所有父节点信息。的主要内容,如果未能解决你的问题,请参考以下文章
怎么把下面的的sql语句查询出来的结果插入到一张新表中去 求大神帮忙