文本检测DB:Real-time Scene Text Detection with Differentiable Binarization

Posted 2022-10-14 超级无敌陈大佬的跟班

目录

网络整体流程

一. Label generation

1.1 probability map生成

1.2 threshold map 生成

二.Differentiable Binarization可微二值化

2.1 传统二值化和DB可微二值化的区别

2.2 ☆可微二值化

2.2.1 可微分的二值化公式：

2.2.2 DB函数反向传播求导的过程

 2.2.3 可微二值化实际计算示例

三. 损失函数

 四、实验结果

---

DB:Real-time Scene Text Detection with Differentiable Binarization

关键创新点：Differentiable Binarization(DB,可微分二值化)，作者提出了一种可微分的二值化方式，相比于传统的二值化操作，DB能够在网络中进行端到端训练。另外还是用可变形卷积用于更好的处理不同长度的文本。

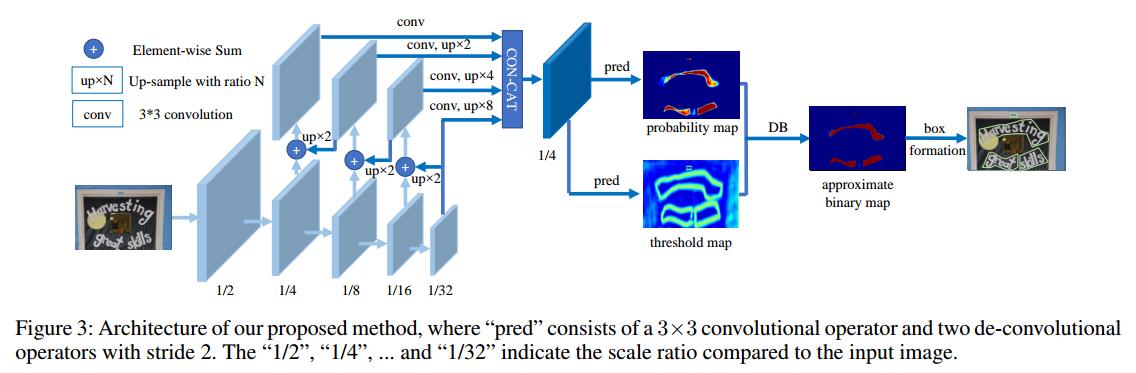
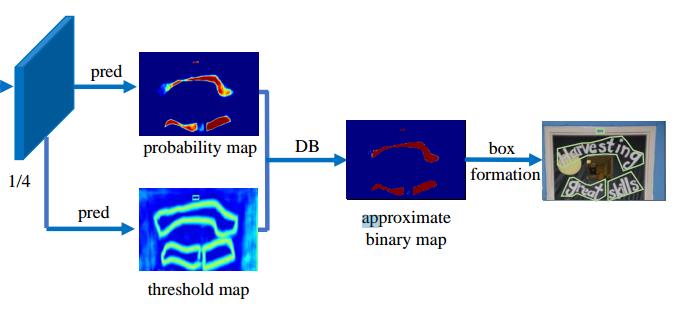
网络整体流程

网络整体流程如下图所示：

• backbone提特征 + FPN结构 进行多尺度图像特征融合
• FPN结构融合特征后会生成两个特征图 probability map(预测图) 跟 threshold map(阈值图)
• 通过probability map 与threshold map 两个特征图做DB差分操作得到文字区域二分图
• 二分图经过cv2 轮廓得到文字区域信息

一. Label generation

label生成的流程图如下所示，特征图 probability map(预测图) 跟 threshold map(阈值图)

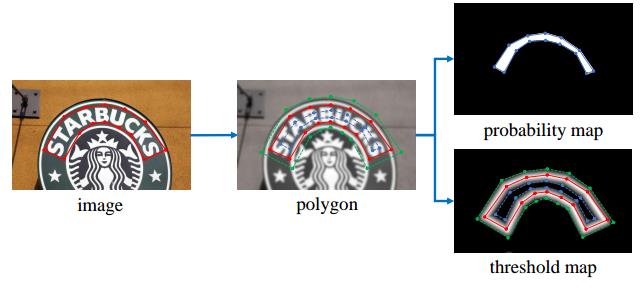
1.1 probability map生成

        使用Vatti clipping algorithm 对gt多边形polygon 进行缩放，将G缩减到Gs（蓝线内部）。probability map中蓝线以内的区域取值为1，其它区域值为0。

        收缩的偏移量D的计算方式：

        偏移量D根据原始多边形(红线区域)的周长L和面积A计算得出的，r是shrink ratio，设置为0.4。

                         

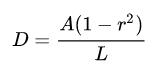
1.2 threshold map 生成

        threshold map使用与生成probability map一样的方法，向外进行扩张，得到绿线和蓝线中间的区域，并根据到红线的距离制作标签，（设置最大值为thresh_max=0.7），其他区域使用thresh_min=0.3进行填充。

• 蓝线以内区域的值为0.3
• 绿线以外区域的值也为0.3
• 绿线和蓝线中间的区域的值，越靠近红线越接近0.7，越远离红线越接近0.3

probability map 的gt是一个完全的0、1 mask ,polygon 的缩小区域为1，其他背景区域为0；

但是在threshold_map文字边框值并非0,1。

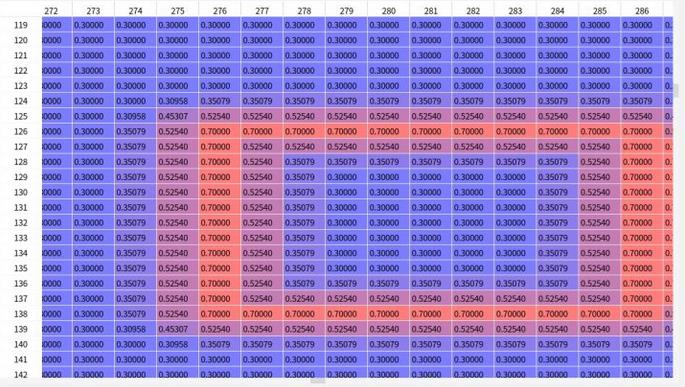
         红色边框为文字区域边框，文字最外圈边缘为0.7，靠近中心区域是为0.3的值。（0.3-0.7为预设的阈值最大最小值）。图中可以看到文字边界处的阈值最大，然后根据文字实例边缘距离逐渐递减。

二.Differentiable Binarization可微二值化

可微二值化(Differentiable Binarization)是论文中的核心创新点.

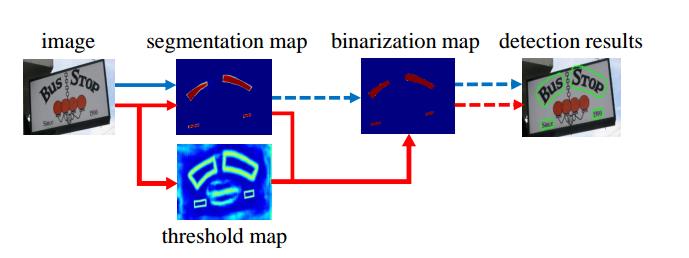
2.1 传统二值化和DB可微二值化的区别

传统二值化操作方式(上图蓝色箭头)：

• 首先，使用一个固定的阈值，用于将segmentation map转换为二值化图像；
• 然后，使用像素聚类等方式将像素分组为文本实例；

DB可微二值化的操作方式(上图红色箭头)：

• 将 segmentation map与threshold map做一次可微分二值化(DB)得到二值化图，然后再经过后处理得到最终结果。
• 将二值化操作放到网络中进行优化，可以自适应地预测图像每个位置的阈值，从而可以将像素与前景和背景完全区分开。 但是，标准二值化函数是不可微分的，因此，本文提出了一种二值化的近似函数，称为可微分二值化（DB），训练阶段该函数完全可微分。

传统二值化公式：

                                         

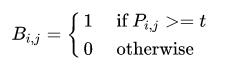
        P_ij代表了probability_map中第i行第j列的概率值。将概率大于某个固定阈值t的像素作为文字像素。

        标准二值化是不可微的。 因此，在训练期间无法与分割网络一起对其进行优化。 为了解决这个问题，作者使用下面的近似阶跃函数(sigmod函数)执行二值化。

2.2 ☆可微二值化

2.2.1 可微分的二值化公式：

                                        

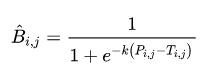
        其中B是近似二值图； T是从网络获知的自适应阈值图； k表示放大因子。 k根据经验设置为50。 该近似二值化函数的行为类似于标准二值化函数，可以在训练期间与分割网络一起进行优化。 具有自适应阈值的可微分二值化不仅可以帮助区分文本区域和背景，还可以分离紧密连接的文本实例。

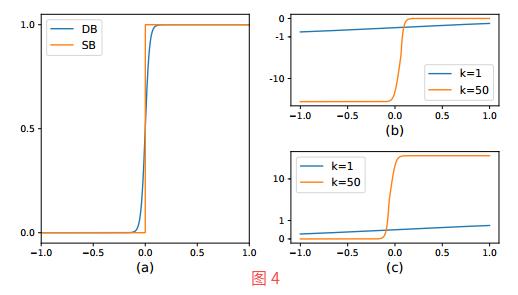
        公式借鉴了sigmod函数的形式将输入映射到0~1之间，将概率值P_ij与阈值T_ij之间的差值作为sigmod函数的X变量，然后再经过放大系数K（取50），将其输出无限逼近两个极端 0 或者1； 如下图所示，SB为标准二值化，DB为可微二值化的函数图像.

                             

2.2.2 DB函数反向传播求导的过程

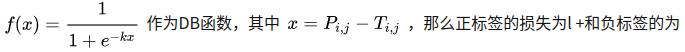
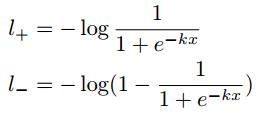
 通过链式求导法则计算正负标签的导数， l+和l-的导数如上图4的(b) (c) 所示。

 2.2.3 可微二值化实际计算示例

        我们来根据label generation中的gt 与 threshold_map来分别计算下。经过这个可微分二值化的sigmod函数后，各个区域的像素值会变成什么样子：

1）文字实例中心区域的像素：

• probability map 的gt为 1
• threshold map的gt值为0.3

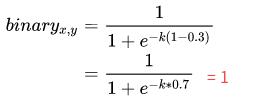
        如果不经过放大系数K的放大，那么区域正中心的像素如上图所示经过sigmod函数后趋向于0.6左右的值。但是经过放大系数k后，会往右倾向于1。 

2）文字实例边缘区域像素：

• probability map 的gt为 1
• threshold map的gt值为0.7

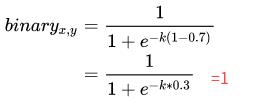
3）文字实例外的像素：

• probability map 的gt为 0
• threshold map的gt值为0.3

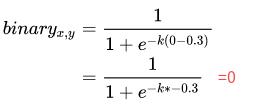
三. 损失函数

1）总的损失函数：

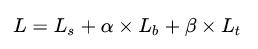
        L_s是probability map的loss，L_b是binary map的loss，L_t是threshold map的loss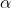，和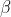设置为1和10。 

2）L_s和L_b为交叉熵损失:

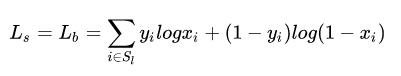
其中S_l表示使用OHEM进行采样，使得正负样本的比例为1：3。 

3）L_t使用L1 Loss，R_d表示绿线以内的区域。

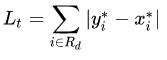
 四、实验结果

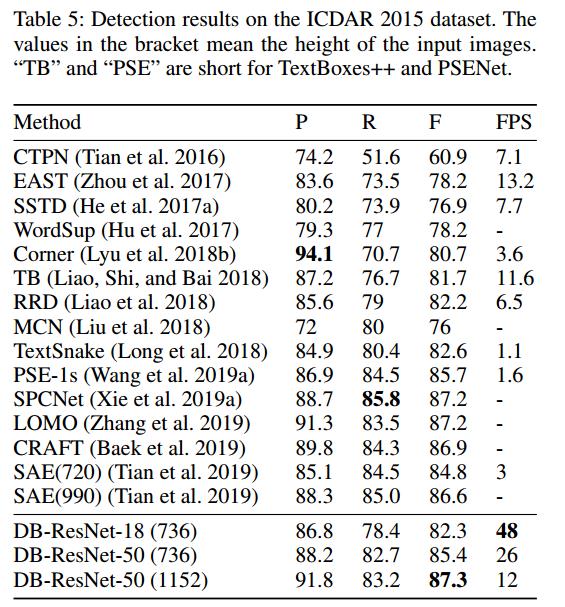
附录：

probability map生成的源码：

# 使用Polygon库计算多边形区域的周长和面积，使用pyclipper库进行shrink
def shrink_polygon_pyclipper(polygon, shrink_ratio):
    from shapely.geometry import Polygon
    import pyclipper
    polygon_shape = Polygon(polygon)
    distance = polygon_shape.area * (1 - np.power(shrink_ratio, 2)) / polygon_shape.length
    subject = [tuple(l) for l in polygon]
    padding = pyclipper.PyclipperOffset()
    padding.AddPath(subject, pyclipper.JT_ROUND, pyclipper.ET_CLOSEDPOLYGON)
    shrinked = padding.Execute(-distance)
    if shrinked == []:
        shrinked = np.array(shrinked)
    else:
        shrinked = np.array(shrinked[0]).reshape(-1, 2)
    return shrinked

threshold map 生成的源码：

'''
# 当前位置到每一条变的距离
absolute_distance = self.distance(xs, ys, polygon[i], polygon[j])
# 规约到[0,1]
distance_map[i] = np.clip(absolute_distance / distance, 0, 1)
# 取该点到各条边的最小值，越靠近响应值越大
distance_map = distance_map.min(axis=0)
# 规约到[0.3,0.7]
canvas = canvas * (self.thresh_max - self.thresh_min) + self.thresh_min
'''
class MakeBorderMap():
    def __init__(self, shrink_ratio=0.4, thresh_min=0.3, thresh_max=0.7):
        self.shrink_ratio = shrink_ratio
        self.thresh_min = thresh_min
        self.thresh_max = thresh_max

    def __call__(self, data: dict) -> dict:
        """
        :param data: 'img':,'text_polys':,'texts':,'ignore_tags':
        :return:
        """
        im = data['img']
        text_polys = data['text_polys']
        ignore_tags = data['ignore_tags']

        canvas = np.zeros(im.shape[:2], dtype=np.float32)
        mask = np.zeros(im.shape[:2], dtype=np.float32)

        for i in range(len(text_polys)):
            if ignore_tags[i]:
                continue
            self.draw_border_map(text_polys[i], canvas, mask=mask)
        # 设置最大值为0.7，最小值为0.3
        canvas = canvas * (self.thresh_max - self.thresh_min) + self.thresh_min

        data['threshold_map'] = canvas
        data['threshold_mask'] = mask
        return data

    def draw_border_map(self, polygon, canvas, mask):
        polygon = np.array(polygon)
        assert polygon.ndim == 2
        assert polygon.shape[1] == 2

        polygon_shape = Polygon(polygon)
        if polygon_shape.area <= 0:
            return
        # 向外扩张
        distance = polygon_shape.area * (1 - np.power(self.shrink_ratio, 2)) / polygon_shape.length
        subject = [tuple(l) for l in polygon]
        padding = pyclipper.PyclipperOffset()
        padding.AddPath(subject, pyclipper.JT_ROUND,
                        pyclipper.ET_CLOSEDPOLYGON)

        padded_polygon = np.array(padding.Execute(distance)[0])
        cv2.fillPoly(mask, [padded_polygon.astype(np.int32)], 1.0)

        xmin = padded_polygon[:, 0].min()
        xmax = padded_polygon[:, 0].max()
        ymin = padded_polygon[:, 1].min()
        ymax = padded_polygon[:, 1].max()
        width = xmax - xmin + 1
        height = ymax - ymin + 1
                
        polygon[:, 0] = polygon[:, 0] - xmin
        polygon[:, 1] = polygon[:, 1] - ymin
                # 生成x、y的loc
        xs = np.broadcast_to(
            np.linspace(0, width - 1, num=width).reshape(1, width), (height, width))
        ys = np.broadcast_to(
            np.linspace(0, height - 1, num=height).reshape(height, 1), (height, width))
                # 根据不同的距离得到不同的值
        distance_map = np.zeros(
            (polygon.shape[0], height, width), dtype=np.float32)
        for i in range(polygon.shape[0]):
            j = (i + 1) % polygon.shape[0]
            absolute_distance = self.distance(xs, ys, polygon[i], polygon[j])
            distance_map[i] = np.clip(absolute_distance / distance, 0, 1)
        distance_map = distance_map.min(axis=0)
                # 将值添加到canvas中
        xmin_valid = min(max(0, xmin), canvas.shape[1] - 1)
        xmax_valid = min(max(0, xmax), canvas.shape[1] - 1)
        ymin_valid = min(max(0, ymin), canvas.shape[0] - 1)
        ymax_valid = min(max(0, ymax), canvas.shape[0] - 1)
        canvas[ymin_valid:ymax_valid + 1, xmin_valid:xmax_valid + 1] = np.fmax(
            1 - distance_map[
                ymin_valid - ymin:ymax_valid - ymax + height,
                xmin_valid - xmin:xmax_valid - xmax + width],
            canvas[ymin_valid:ymax_valid + 1, xmin_valid:xmax_valid + 1])

    def distance(self, xs, ys, point_1, point_2):
        '''
        compute the distance from point to a line
        ys: coordinates in the first axis
        xs: coordinates in the second axis
        point_1, point_2: (x, y), the end of the line
        '''
        height, width = xs.shape[:2]
        square_distance_1 = np.square(xs - point_1[0]) + np.square(ys - point_1[1])
        square_distance_2 = np.square(xs - point_2[0]) + np.square(ys - point_2[1])
        square_distance = np.square(point_1[0] - point_2[0]) + np.square(point_1[1] - point_2[1])

        cosin = (square_distance - square_distance_1 - square_distance_2) / (2 * np.sqrt(square_distance_1 * square_distance_2))
        square_sin = 1 - np.square(cosin)
        square_sin = np.nan_to_num(square_sin)

        result = np.sqrt(square_distance_1 * square_distance_2 * square_sin / square_distance)
        result[cosin < 0] = np.sqrt(np.fmin(square_distance_1, square_distance_2))[cosin < 0]
        # self.extend_line(point_1, point_2, result)
        return result

参考文档：

 文字检测（三）Differentiable Binarization论文阅读 - 知乎

[AAAI2020]论文翻译DB:Real-time Scene Text Detection with Differentiable Binarization - 简书

可微二值化的实时场景文本检测 - 知乎

DB：Real-time Scene Text Detection with Differentiable Binarization - 简书