神经网络与深度学习 作业3:分别使用numpy和pytorch实现FNN例题
Posted Jacobson Cui
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了神经网络与深度学习 作业3:分别使用numpy和pytorch实现FNN例题相关的知识,希望对你有一定的参考价值。
目录
1、对比【numpy】和【pytorch】程序,总结并陈述。
2、激活函数Sigmoid用PyTorch自带函数torch.sigmoid(),观察、总结并陈述。
3、激活函数Sigmoid改变为Relu,观察、总结并陈述。
4、损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代,观察、总结并陈述。
7、权值w1-w8初始值换为随机数,对比“指定权值”的结果,观察、总结并陈述。
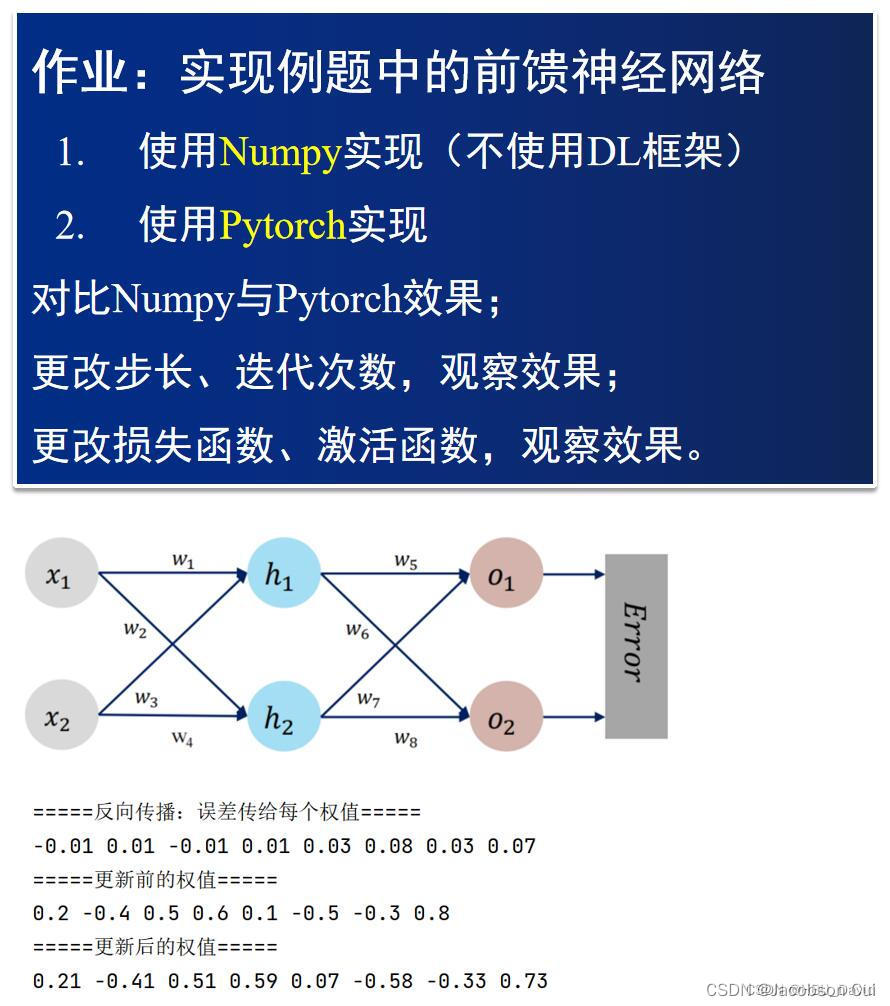
过程推导——了解BP原理
BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络。
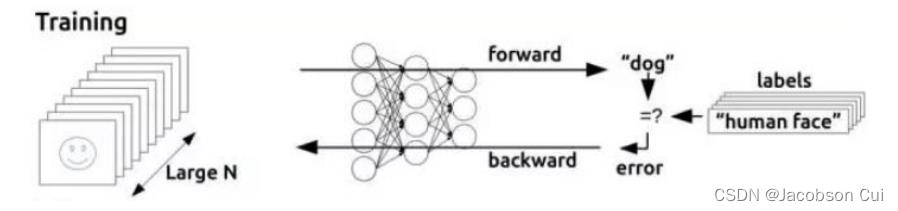
BP算法的学习过程由前向传播过程和反向传播过程组成。在前向传播过程中,输入信息通过输入层经隐含层,逐层处理并传向输出层。如果在输出层得不到期望的输出值,则取输出与期望的误差的平方和作为目标函数,转入反向传播,逐层求出目标函数对各神经元权值的偏导数,构成目标函数对权值向量的梯度,作为修改权值的依据,网络的学习在权值修改过程中完成。误差达到所期望值时,网络学习结束。如图所示为BP算法模型示意图:

推导过程:(还不太习惯用平板写字,字比较丑请见谅^_^)

数值计算
将题目中给出的数值代入推导出的公式中
以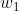 为例:
为例:

代码实现
使用numpy实现
import numpy as np
w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8
x1, x2 = 0.5, 0.3
y1, y2 = 0.23, -0.07
print("输入值 x0, x1:")
print(x1, x2)
print("输出值 y0, y1:")
print(y1, y2)
def sigmoid(z):
a = 1 / (1 + np.exp(-z))
return a
def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2)
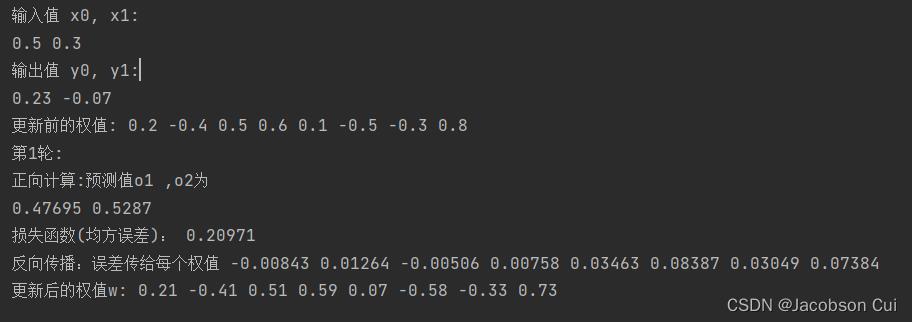
print("正向计算:预测值o1 ,o2为")
print(round(out_o1, 5), round(out_o2, 5))
error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2
print("损失函数(均方误差):",round(error, 5))
return out_o1, out_o2, out_h1, out_h2
def back_propagate(out_o1, out_o2, out_h1, out_h2):
# 反向传播
d_o1 = out_o1 - y1
d_o2 = out_o2 - y2
d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
d_w1 = (d_o1 * out_h1 * (1 - out_h1) * w5 + d_o2 * out_o2 * (1 - out_o2) * w6) * out_h1 * (1 - out_h1) * x1
d_w3 = (d_o1 * out_h1 * (1 - out_h1) * w5 + d_o2 * out_o2 * (1 - out_o2) * w6) * out_h1 * (1 - out_h1) * x2
d_w2 = (d_o1 * out_h1 * (1 - out_h1) * w7 + d_o2 * out_o2 * (1 - out_o2) * w8) * out_h2 * (1 - out_h2) * x1
d_w4 = (d_o1 * out_h1 * (1 - out_h1) * w7 + d_o2 * out_o2 * (1 - out_o2) * w8) * out_h2 * (1 - out_h2) * x2
print("反向传播:误差传给每个权值", round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
round(d_w7, 5), round(d_w8, 5))
return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1 = w1 - step * d_w1
w2 = w2 - step * d_w2
w3 = w3 - step * d_w3
w4 = w4 - step * d_w4
w5 = w5 - step * d_w5
w6 = w6 - step * d_w6
w7 = w7 - step * d_w7
w8 = w8 - step * d_w8
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
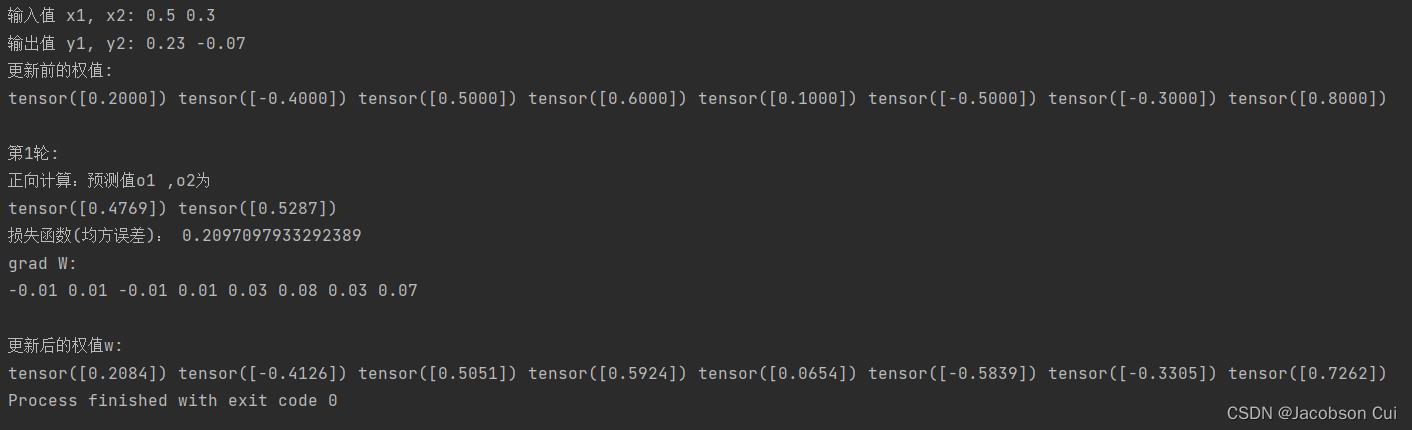
print("更新前的权值:",round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
round(w8, 2))
for i in range(1):
print("第" + str(i+1) + "轮:")
out_o1, out_o2, out_h1, out_h2 = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值w:", round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
round(w8, 2))
运行结果:
使用pytorch实现
import torch
x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值:x1, x2;真实输出值:y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
[0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8]) # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2 # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss.item())
return loss
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意:将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(1):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播,求 Loss,构建计算图
L.backward() # 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
print("\\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
运行结果:
1、对比【numpy】和【pytorch】程序,总结并陈述。
通过改变训练轮数,发现无论训练多少轮,还是当梯度都为0时(即找到最优解),结果都十分相近,因此可认为两种方法的求解效果基本相同。
例如:
训练轮数等于2时【numpy】程序结果:

训练轮数等于2时【pytorch】程序结果:

2、激活函数Sigmoid用PyTorch自带函数torch.sigmoid(),观察、总结并陈述。
使用Sigmoid函数和使用Pytorch自带函数torch.sigmoid()没较为明显的差距。
3、激活函数Sigmoid改变为Relu,观察、总结并陈述。
训练2轮Sigmoid函数:
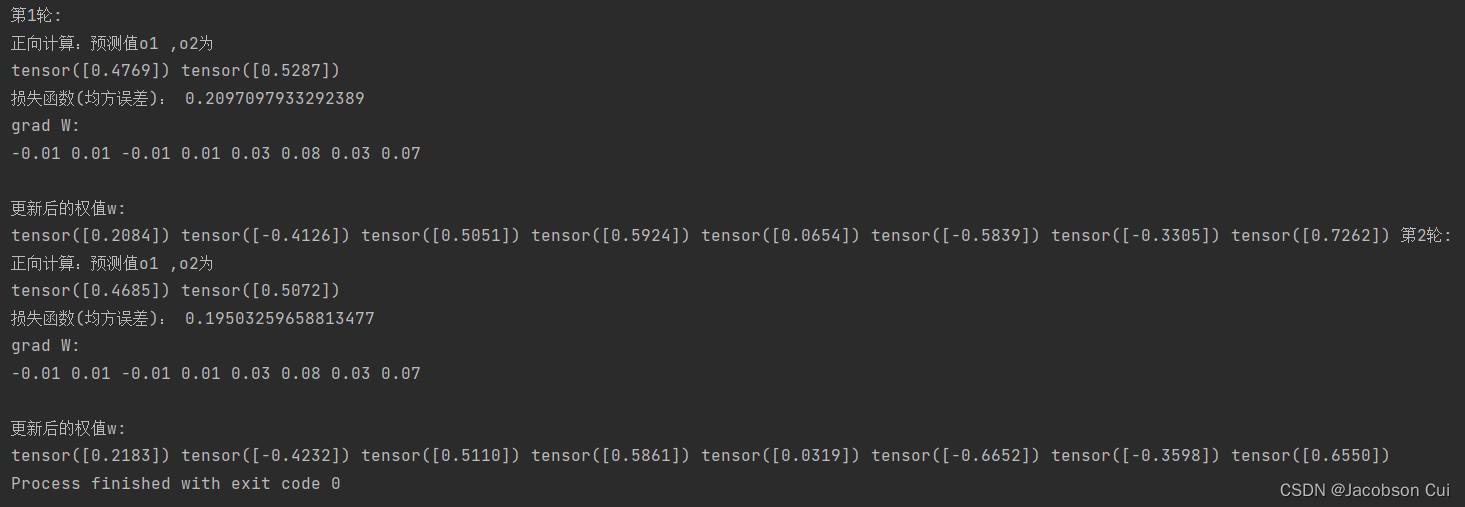
训练2轮Relu函数:
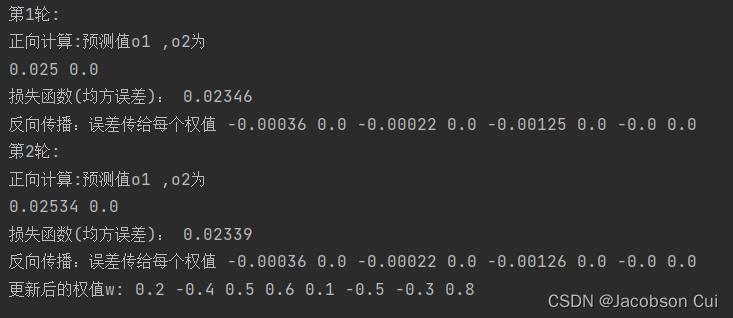
和sigmoid函数相比,Relu函数均方误差降低速度快,因此使用Relu激活函数收敛速度要优于使用sigmoid激活函数。
def sigmoid(z):
a = 1 / (1 + np.exp(-z))
return adef relu(z):
return np.maximum(0, z)(1)作为激活函数,计算简单,更加高效,速度快
神经元得到一个值,可以直接看这个值的大小,然后直接得出结果,不用多余的加减乘除计算
单侧抑制,小于0全部抑制;宽兴奋边界,大于0的部分达到无穷都可以,没有限制,即兴奋程度可以很高;有很好的稀疏性,能让小于0的全部变为0,增大了稀疏性。
ReLU的一个重要优势是它能够输出真正的零值。 这与Sigmoid激活函数不同,后者学习近似零输出,例如非常接近零的值,但不是真正的零值。 这意味着负输入可以输出真实零值, 从而允许神经网络中的隐藏层激活以包含一个或多个真实零值。
4、损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代,观察、总结并陈述。
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
loss_func = torch.nn.MSELoss() # 创建损失函数
y_pred = torch.cat((y1_pred, y2_pred), dim=0) # 将y1_pred, y2_pred合并成一个向量
y = torch.cat((y1, y2), dim=0) # 将y1, y2合并成一个向量
loss = loss_func(y_pred, y) # 计算损失
print("损失函数(均方误差):", loss.item())
return loss通过运行结果观察发现自带函数和原先编写的函数运行结果相同。
5、损失函数MSE改变为交叉熵,观察、总结并陈述。
def loss_fuction(x1, x2, y1, y2):
y1_pred, y2_pred = forward_propagate(x1, x2)
loss_func = torch.nn.CrossEntropyLoss() # 创建交叉熵损失函数
y_pred = torch.stack([y1_pred, y2_pred], dim=1)
y = torch.stack([y1, y2], dim=1)
loss = loss_func(y_pred, y) # 计算
print("损失函数(交叉熵损失):", loss.item())
return loss 运行结果:
改为交叉熵之后损失函数出现负数
6、改变步长,训练次数,观察、总结并陈述。
step=1:
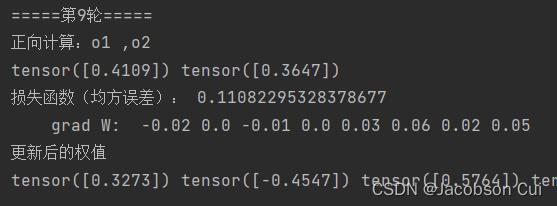
step=10:
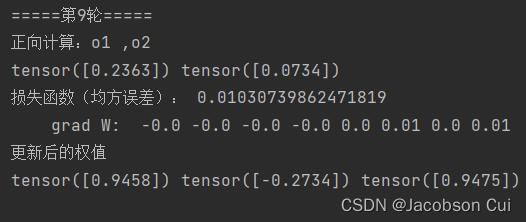
可见,步长越大,均方误差下降越快,收敛就越快;
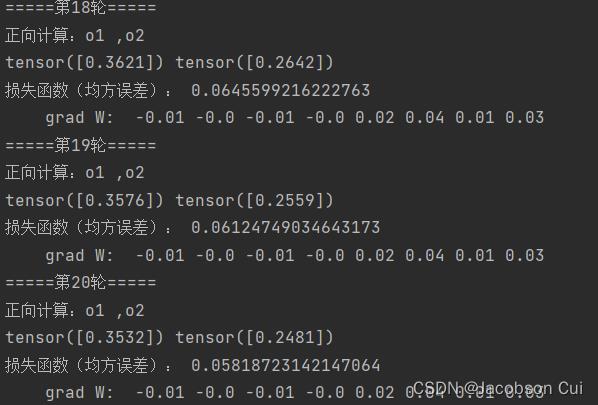
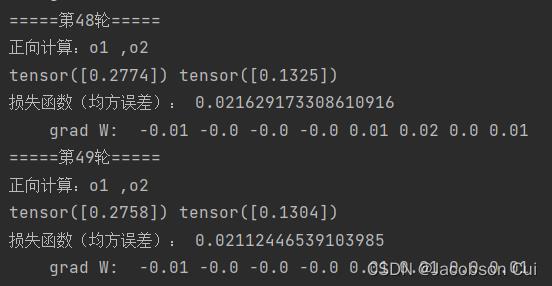
改变步数发现,随着步数的增大,均方误差下降速度也在逐渐降低,收敛速度下降
7、权值w1-w8初始值换为随机数,对比“指定权值”的结果,观察、总结并陈述。
指定权值 :
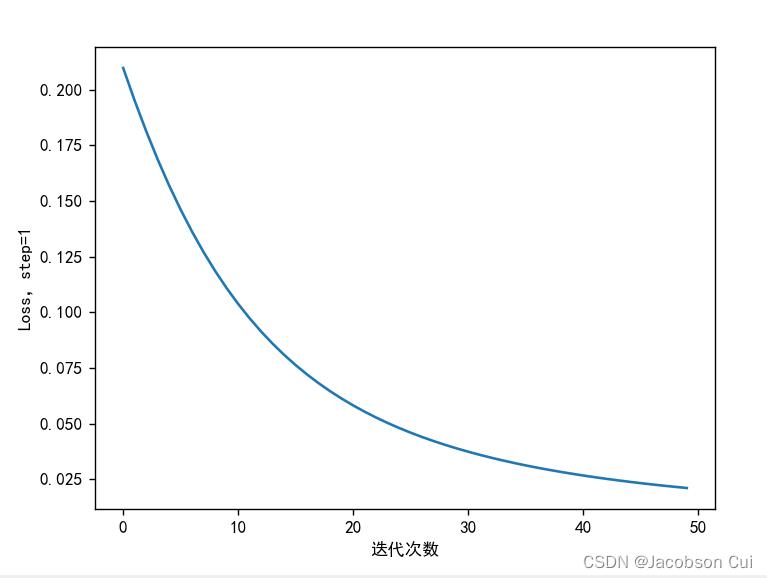
随机数: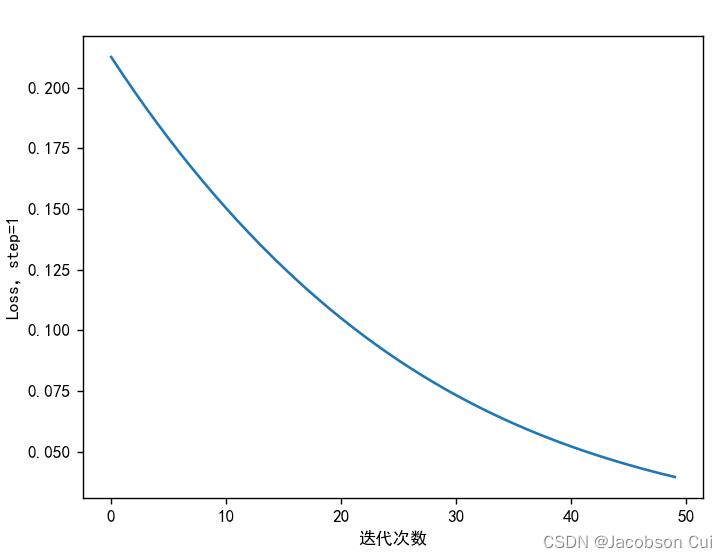
由图可见,当w1-w8初始值换为随机数后,均方误差的下降速度与指定权值时相比有所降低,收敛速度小于指定权值。
8、权值w1-w8初始值换为0,观察、总结并陈述。
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor(
[0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0])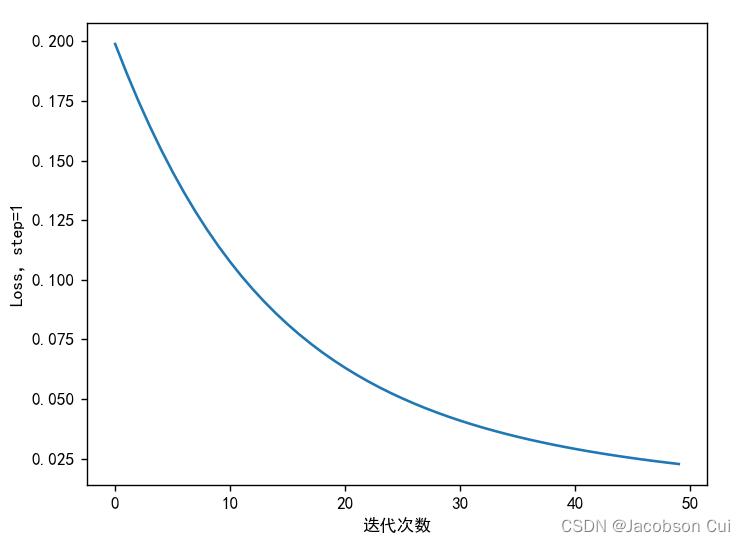
w1-w8初始值换为0,对收敛速度没有影响。
9、心得体会
在上学期的机器学习课程里面就接触过反向传播算法,但当时掌握得并不是很好,通过这次作业,对公式进行了推导并再一次翻看了周志华老师的西瓜书里相应的内容,使我对反向传播算法理解得到了进一步的加深,通过习题也详细了解到了各个参数以及激活函数的改变对结果的影响。
参考
“反向传播算法”过程及公式推导_aift的博客-CSDN博客_反向传播算法
【2021-2022 春学期】人工智能-作业2:例题程序现_HBU_David的博客-CSDN博客
【2021-2022 春学期】人工智能-作业3:例题程序复现 PyTorch版_HBU_David的博客-CSDN博客
以上是关于神经网络与深度学习 作业3:分别使用numpy和pytorch实现FNN例题的主要内容,如果未能解决你的问题,请参考以下文章