机器学习数据的预处理

Posted 2022-09-28 我爱Python数据挖掘

内容如下

• • 数据清洗
  • • 1、重复观测处理
    • 2、缺失值处理
  • 删减特征
  • • 1\\. 去除唯一属性
  • 数据查看
  • 特征缩放
  • • 1、为什么要特征数据缩放？
    • 2、特征缩放常用的方法
    • • 1、归一化
      • 2、标准化
      • 相同点及其联系

本文技术来自技术群小伙伴的推荐，加入按照如下方式

目前开通了技术交流群，群友已超过3000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友
方式①、添加微信号：dkl88191，备注：来自CSDN+技术交流
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：加群+CSDN

数据清洗

在数据处理过程中，一般都需要进行数据的清洗工作，如数据集是否存在重复、是否存在缺失、 数据是否具有完整性和一致性、数据中是否存在异常值等。

1、重复观测处理

data=pd.DataFrame([[8.3,6],[9.3,4],[6,8],[3,1],[3,1]])

print('数据集中是否存在重复观测：\\n',any(data.duplicated()))

data.drop_duplicates(inplace = True)

print('数据集中是否存在重复观测：\\n',any(data.duplicated()))

2、缺失值处理

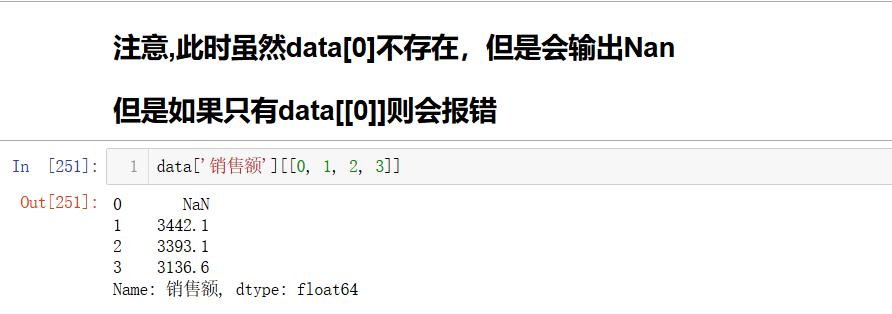
一般而言，当遇到缺失值（Python中用NaN 表示）时，可以采用三种方法处置，分别是删除法、替换法和插补法。

• 删除法

data=pd.DataFrame([[8.3,6,],[9.3,4,],[6,8,8],[5,6],[3,1,8]],columns=('a','b','c'))

print('数据集中是否存在缺失值：\\n',any(data.isnull()))

data.drop(["c"],axis =1 ,inplace=True)

data=data.dropna(axis=0,how='any')

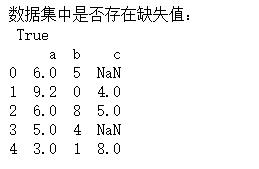
解析：

​​​​​1、删除全为空值的行或列

  data=data.dropna(axis=0,how='all')   #行

  data=data.dropna(axis=1,how='all')   #列

2、删除含有空值的行或列

 data=data.dropna(axis=0,how='any')   #行

data=data.dropna(axis=1,how='any')   #列

函数具体解释：

DataFrame.dropna(axis=0, how=‘any’, thresh=None, subset=None, inplace=False)
函数作用：删除含有空值的行或列

axis：维度，axis=0表示index行,axis=1表示columns列，默认为0

how："all"表示这一行或列中的元素全部缺失（为nan）才删除这一行或列，"any"表示这一行或列中只要有元素缺失，就删除这一行或列

thresh：一行或一列中至少出现了thresh个才删除。

subset：在某些列的子集中选择出现了缺失值的列删除，不在子集中的含有缺失值得列或行不会删除（有axis决定是行还是列）

inplace：刷选过缺失值得新数据是存为副本还是直接在原数据上进行修改。

• 替换法

#data.fillna(method = 'ffill')

#data.fillna(method = 'bfill')

#data['c']=data['c'].fillna(data['c'].mean())

#data['c']=data['c'].fillna(data['c'].mode())

data['c']=data['c'].fillna(data['c'].median())

• 插补法

插值法是利用已知点建立合适的插值函数，未知值由对应点xi求出的函数值f(xi)近似代替，常用的有格朗日插值法、牛顿插值法、均值/中位数/众数插补、使用固定值、最近插补、回归方法等

我用格朗日插值法来举个例子：在餐饮系统中的销售量可能会出现缺失值，我们使用拉格朗日插值法对缺失的数据进行填补。

时间	2015/2/25	2015/2/24	2015/2/23	2015/2/22	2015/2/21	2015/2/20
销售额	3442.1	3393.1	3136.6	3744.1	6607.4	4060.3

时间	2015/2/19	2015/2/18	2015/2/16	2015/2/15	2015/2/14	2015/2/13
销售额	3614.7	3295.5	2332.1	2699.3	空值	3036.8

import pandas as pd

from scipy.interpolate import lagrange

inputfile = '../data/catering_sal.xls'
outfile = '../tmp/sales.xls'

data = pd.read_excel(inputfile)

data['销量'][(data['销量'] < 400) | (data['销量'] > 5000)] = None

def ployinterp_columns(s, n, k=5 ):
	y = s[list(range(n-k, n)) + list[range(n+1, n+1+k)]] 
	y = y[y.notnull()] 
	return lagrange(y.index, list(y))(n) 


for i in data.columns:
	for j in range(len(data)):
		if (data[i].isnull())[j]: 
			data[i][j] = ployinterp_column(data[i], j)
data.to_excle(outputfile) 

使用拉格朗日插值法对缺失值进行插补，使用缺失值前后5个未缺失的数据参与建模，在进行插值之前，会对数据进行异常值检测，发现2015/2/21日的数据是异常的（数据大于5000）， 所以把该日期数据定义为空缺值，利用拉格朗日插值对2015/2/21， 2015/2/14的数据进行插补，结果是4275.255和4156.86， 这两天使周末，而周末的销售额一般要大于周一到周五的值，所以插值的结果比较符合实际情况。

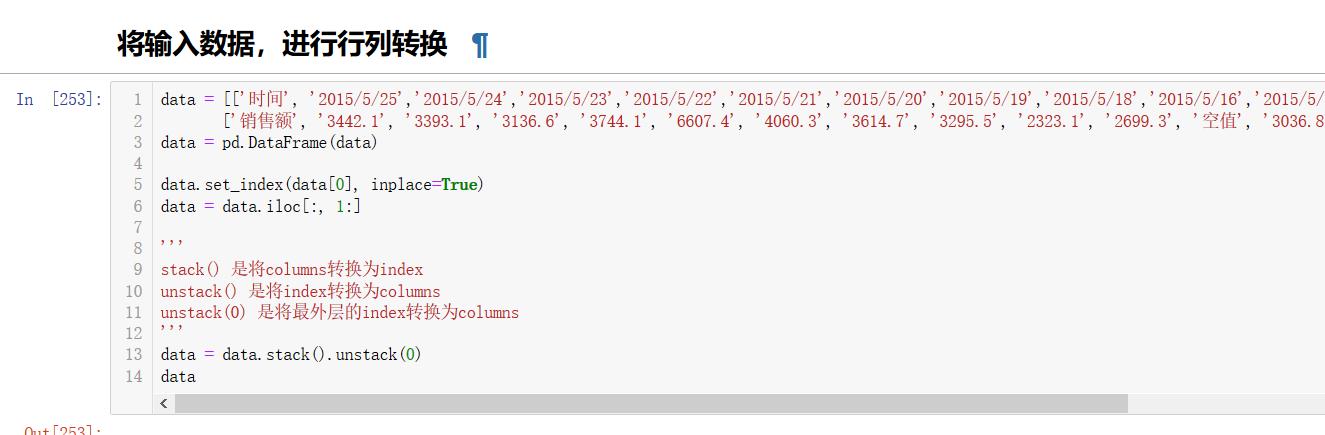
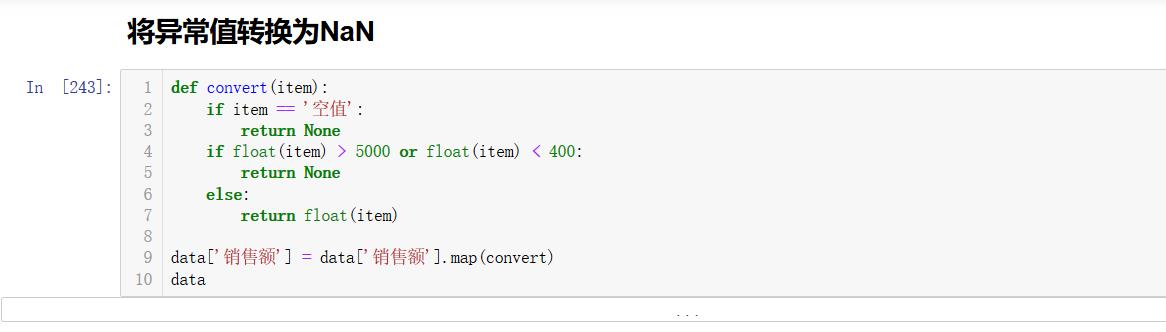
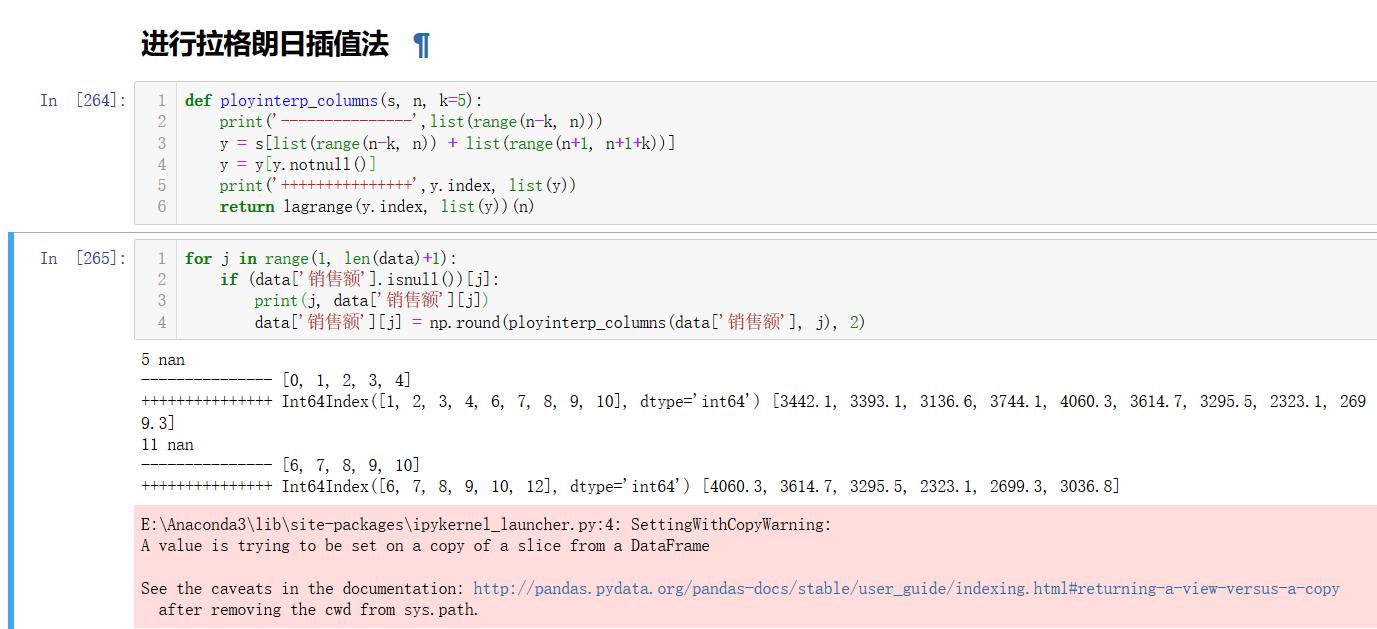
删减特征

1. 去除唯一属性

唯一属性通常是一些id属性，这些属性并不能刻画样本自身的分布规律，所以简单地删除这些属性即可。

数据查看

• 查看行列： data.shape
• 查看数据详细信息： data.info()，可以查看是否有缺失值
• 查看数据的描述统计分析： data.describe()，可以查看到异常数据
• 获取前/后10行数据： data.head(10)、data.tail(10)
• 查看列标签： data.columns.tolist()
• 查看行索引： data.index
• 查看数据类型： data.dtypes
• 查看数据维度： data.ndim
• 查看除index外的值： data.values，会以二维ndarray的形式返回DataFrame的数据
• 查看数据分布（直方图）： seaborn.distplot(data[列名].dropna())

特征缩放

1、为什么要特征数据缩放？

有特征的取值范围变化大，影响到其他的特征取值范围较小的，那么，根据欧氏距离公式，整个距离将被取值范围较大的那个特征所主导。

为避免发生这种情况，一般对各个特征进行缩放，比如都缩放到[0,1]，以便每个特征属性对距离有大致相同的贡献。

作用： 确保这些特征都处在一个相近的范围。

优点： 1、这能帮助梯度下降算法更快地收敛，2、提高模型精度

直接求解的缺点：
1、当x1 特征对应权重会比x2 对应的权重小很多，降低模型可解释性
2、梯度下降时，最终解被某个特征所主导，会影响模型精度与收敛速度
3、正则化时会不平等看待特征的重要程度（尚未标准化就进行L1/L2正则化是错误的）

哪些机器学习算法不需要(需要)做归一化?

概率模型（树形模型）不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、RF。而像Adaboost、SVM、LR、Knn、KMeans之类的最优化问题就需要归一化。

2、特征缩放常用的方法

1、归一化

• 数值的归一，丢失数据的分布信息，对数据之间的距离没有得到较好的保留，但保留了权重。
• 1.小数据/固定数据的使用；2.不涉及距离度量、协方差计算、数据不符合正态分布的时候；3.进行多指标综合评价的时候。

将数值规约到(0,1)或(-1,1)区间。

一个特征X的范围[min，max]

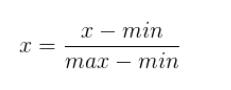
data=pd.DataFrame([[8.3,6],[9.3,4],[6,8],[3,1]])

data[0]=(data[0]-data[0].min())/(data[0].max()-data[0].min())

data[1]=(data[1]-data[1].min())/(data[1].max()-data[1].min())

结果：

2、标准化

• 数据分布的归一，较好的保留了数据之间的分布，也即保留了样本之间的距离，但丢失了权值
• 1.在分类、聚类算法中，需要使用距离来度量相似性；2.有较好的鲁棒性，有产出取值范围的离散数据或对最大值最小值未知的情况下。

将数据变换为均值为0，标准差为1的分布切记，并非一定是正态的。

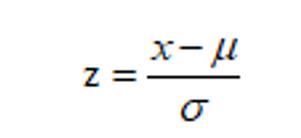
其中μ为所有样本数据的均值，σ为所有样本数据的标准差。

先求均值（mean）

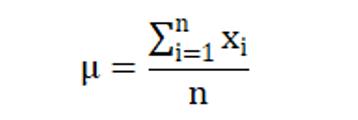
再求方差（std）

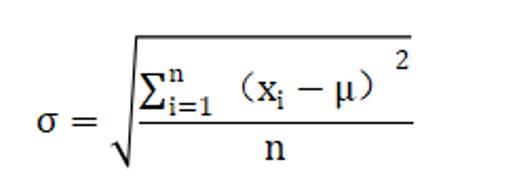
from sklearn.preprocessing import StandardScaler

data=np.array([[2,2,3],[1,2,5]])

# transform函数则是利用这两个值来标准化（转换）

结果：

大家可以用以上公式进行验证一下

这两组数据的均值是否为0，方差（σ2）是否为1

相同点及其联系

• 归一化广义上是包含标准化的，以上主要是从狭义上区分两者。本质上都是进行特征提取，方便最终数据的比较。都是为了缩小范围，便于后续的数据处理。
• 加快梯度下降，损失函数收敛； 提升模型精度； 防止梯度爆炸(消除因为输入差距过大而带来的输出差距过大，进而在反向传播的过程当中导致梯度过大，从而形成梯度爆炸)