怎样求最大公约数？

Posted 2023-04-18

您好，在求最大公约数时,一般先用最小的公约数去除,直到得数为互质数时为止,再将所有的公约数相乘,积就是几个数的最大公约数。

举个例子：

以12和16为例，两者先都除以2，得6,8。

6和8还可以继续除以2，得到3,4。

3,4互为质数，不可再除。

所以12,和16的最大公约数就等于2乘2，得4。

最大公因数，也称最大 公约数、最大公 因子，指两个或多个 整数共有 约数中最大的一个。 a， b的最大公约数记为（a，b），同样的，a，b，c的最大 公约数记为（a，b，c），多个 整数的最大公约数也有同样的记号。求最大公约数有多种 方法，常见的有 质因数分解法、 短除法、 辗转相除法、 更相减损法。与最大公约数相对应的概念是 最小公倍数，a，b的 最小公倍数记为[a，b]。

参考技术A

最普遍的介绍：

最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。

a，b的最大公约数记为（a，b），同样的，a，b，c的最大公约数记为（a，b，c），多个整数的最大公约数也有同样的记号。求最大公约数有多种方法，常见的有质因数分解法、短除法、辗转相除法、更相减损法。与最大公约数相对应的概念是最小公倍数，a，b的最小公倍数记为[a，b]。

【拓展资料】

一、基本概念及举例说明：

1、如果数a能被数b整除，a就叫做b的倍数，b就叫做a的约数。约数和倍数都表示一个整数与另一个整数的关系，不能单独存在。

举例：只能说16是某数的倍数，2是某数的约数，而不能孤立地说16是倍数，2是约数。

2、“倍”与“倍数”是不同的两个概念，“倍”是指两个数相除的商，它可以是整数、小数或者分数。“倍数”只是在数的整除的范围内，相对于“约数”而言的一个数字的概念，表示的是能被某一个自然数整除的数。

3、几个整数中公有的约数，叫做这几个数的公约数；其中最大的一个，叫做这几个数的最大公约数。

举例：12、16的公约数有1、2、4，其中最大的一个是4，4是12与16的最大公约数，一般记为（12，16）=4。12、15、18的最大公约数是3，记为（12，15，18）=3。

4、几个自然数公有的倍数，叫做这几个数的公倍数，其中最小的一个自然数，叫做这几个数的最小公倍数。

举例：4的倍数有4、8、12、16，……，6的倍数有6、12、18、24，……，4和6的公倍数有12、24，……，其中最小的是12，一般记为[4，6]=12。12、15、18的最小公倍数是180。记为[12，15，18]=180。若干个互质数的最小公倍数为它们的乘积的绝对值。

二、最大公约数的常见求法

1、质因数分解法

思路：把每个数分别分解质因数，再把各数中的全部公有质因数提取出来连乘，所得的积就是这几个数的最大公约数。

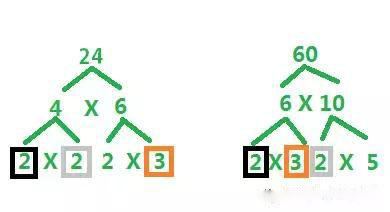
举例：假设我们求24和60的最大公约数。

第一步：分解24和60。

24=2X2X2X3

60=2X3X2X5

第二步：24和60的最大公约数=24和60共有的公因子相乘，即2X2X3=12。

2、短除法

思路：短除法求最大公约数，先用这几个数的公约数连续去除，一直除到所有的商互质为止，然后把所有的除数连乘起来，所得的积就是这几个数的最大公约数。

短除法的本质就是质因数分解法，只是将质因数分解用短除符号来进行。

举例：

12的因数有：1、2、3、4、6、12。

18的因数有：1、2、3、6、9、18。

12与18的公因数有：1、2、3、6。

12与18的最大公因数是6。

3、更相减损法

思路：

第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。

第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。

则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。

举例：

用更相减损术求98与63的最大公约数。

由于63不是偶数，把98和63以大数减小数，并辗转相减：

98-63=35

63-35=28

35-28=7

28-7=21

21-7=14

14-7=7

所以，98和63的最大公约数等于7。

4、辗转相除法

用较小数除较大数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是0为止。如果是求两个数的最大公约数，那么最后的除数就是这两个数的最大公约数。

举例：

求（319，377）：

∵ 319÷377=0（余319）

∴（319，377）=（377，319）；

∵ 377÷319=1（余58）

∴（377，319）=（319，58）；

∵ 319÷58=5（余29）

∴ （319，58）=（58，29）；

∵ 58÷29=2（余0）

∴ （58，29）= 29；

∴ （319，377）=29。

参考技术B 如果有一个自然数a能被自然数b整除，则称a为b的倍数，b为a的约数。几个自然数公有的约数，叫做这几个自然数的公约数。公约数中最大的一个公约数，称为这几个自然数的最大公约数。
这个有几种方法，下面是两种不错的方法：
（1）求差判定法．

如果两个数相差不大，可以用大数减去小数，所得的差与小数的最大公约数就是原来两个数的最大公约数．例如：求78和60的最大公约数．78－60＝18，18和60的最大公约数是6，所以78和60的最大公约数是6．

如果两个数相差较大，可以用大数减去小数的若干倍，一直减到差比小数小为止，差和小数的最大公约数就是原来两数的最大公约数．例如：求92和16的最大公约数．92－16＝76，76－16＝60，60－16＝44，44－16＝28，28－16＝12，12和16的最大公约数是4，所以92和16的最大公约数就是4．

（2）辗转相除法．

当两个数都较大时，采用辗转相除法比较方便．其方法是：

以小数除大数，如果能整除，那么小数就是所求的最大公约数．否则就用余数来除刚才的除数；再用这新除法的余数去除刚才的余数．依此类推，直到一个除法能够整除，这时作为除数的数就是所求的最大公约数．

例如：求4453和5767的最大公约数时，可作如下除法．

5767÷4453＝1余1314

4453÷1314＝3余511

1314÷511＝2余292

511÷292＝1余219

292÷219＝1余73

219÷73＝3

于是得知，5767和4453的最大公约数是73．

辗转相除法适用比较广，比短除法要好得多，它能保证求出任意两个数的最大公约数． 参考技术C 一、自然数的最大公约数的定义可以扩展到分数。一组分数的最大公约数一定是分数，而这组分数分别除以它们的最大公约数应得整数。求一组分数的最大公约数的方法是：
　　1、先将各个分数化为假分数；
　　2、求出各个分数的分母的最小公倍数a；
　　3、求出各个分数的分子的最大公约数b；
　　4、 a/b即为所求。
　　如：求5/6、 2又1 /7 这两个分数的最大公约数。
　　这两个分数化成假分数后是：（5/6，15/7）
　　分母的最小公倍数是：（6，7） ＝42；
　　分子的最大公约数是：（5，15）＝5 ；
　　所以，这四个分数的最大公约数是：5/42
　　二、最大公约数：
　　最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。a，b的最大公约数记为（a，b），同样的，a，b，c的最大公约数记为（a，b，c），多个整数的最大公约数也有同样的记号。
　　求最大公约数有多种方法，常见的有质因数分解法、短除法、辗转相除法、更相减损法。 参考技术D 质因数分解法：把每个数分别分解质因数，再把各数中的全部公有质因数提取出来连乘，所得的积就是这几个数的最大公约数。

短除法：短除法求最大公约数，先用这几个数的公约数连续去除，一直除到所有的商互质为止，然后把所有的除数连乘起来，所得的积就是这几个数的最大公约数。

最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。a，b的最大公约数记为（a，b），同样的，a，b，c的最大公约数记为（a，b，c），多个整数的最大公约数也有同样的记号。求最大公约数有多种方法，常见的有质因数分解法、短除法、辗转相除法、更相减损法。与最大公约数相对应的概念是最小公倍数，a，b的最小公倍数记为[a，b]。

如果数a能被数b整除，a就叫做b的倍数，b就叫做a的约数。约数和倍数都表示一个整数与另一个整数的关系，不能单独存在。如只能说16是某数的倍数，2是某数的约数，而不能孤立地说16是倍数，2是约数。

　"倍"与"倍数"是不同的两个概念，"倍"是指两个数相除的商，它可以是整数、小数或者分数。"倍数"只是在数的整除的范围内，相对于"约数"而言的一个数字的概念，表示的是能被某一个自然数整除的数。
　　
几个整数中公有的约数，叫做这几个数的公约数；其中最大的一个，叫做这几个数的最大公约数。例如：12、16的公约数有1、2、4，其中最大的一个是4，4是12与16的最大公约数，一般记为（12，16）=4。12、15、18的最大公约数是3，记为（12，15，18）=3。

几个自然数公有的倍数，叫做这几个数的公倍数，其中最小的一个自然数，叫做这几个数的最小公倍数。例如：4的倍数有4、8、12、16，……，6的倍数有6、12、18、24，……，4和6的公倍数有12、24，……，其中最小的是12，一般记为[4，6]=12。12、15、18的最小公倍数是180。记为[12，15，18]=180。若干个互质数的最小公倍数为它们的乘积的绝对值。

求圆周率的计算公式？

想练下自己的记忆力，听说记圆周率的倍数是个办法。

最有可能是使用连分数法:由于求二自然数的最大公约数的更相减损术远在《九章算术》成书时代已流行，所以借助这一工具求近似分数应该是比较自然的。于是有人提出祖冲之可能是在求得盈二数之后，再使用这个工具，将3.14159265表示成连分数，得到其渐近分数：3，22／7，333／106，355／113，102573／32650… 最后，取精确度很高但分子分母都较小的355／113作为圆周率的近似值。若是对这些感兴趣可以上网找找，这里有个网站仅供参考 http://zhidao.baidu.com/question/29237343.html 参考技术A 圆周率（Pi）是圆的周长与直径的比值，公式为：
圆周率用希腊字母
π（读作pài）表示，是一个常数（约等于3.141592654），是代表圆周长和直径的比值。它是一个无理数，即无限不循环小数。
在日常生活中，通常都用3.14代表圆周率去进行近似计算。而用十位小数3.141592654便足以应付一般计算。即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百个位。
扩展资料
把圆周率的数值算得这么精确，实际意义并不大。现代科技领域使用的圆周率值，有十几位已经足够了。如果以39位精度的圆周率值，来计算宇宙（observable
universe）的大小，误差还不到一个原子的体积
。
以前的人计算圆周率，是要探究圆周率是否循环小数。自从1761年兰伯特证明了圆周率是无理数，1882年林德曼证明了圆周率是超越数后，圆周率的神秘面纱就被揭开了。
π在许多数学领域都有非常重要的作用。
参考资料来源：百度百科-圆周率
（圆的周长与直径的比值） 参考技术B

圆周率的计算公式有以下几个：

1、马青公式　π=16arctan1/5-4arctan1/239

2、拉马努金公式

3、AGM（Arithmetic-Geometric Mean）算法  高斯-勒让德公式

4、波尔文四次迭代式

5、bailey-borwein-plouffe算法

6、丘德诺夫斯基公式　

7、莱布尼茨公式

圆周率的记忆方法：

【中文背圆周率的口诀】
1π=3.14 

2π=6.28

3π=9.42 

4π=12.56

5π=15.7

6π=18.84

7π=21.98

8π=25.12

参考技术C 就是把圆的内接三角形的面积算出来，让它近似等于圆的面积，然后利用大学的无限思想可以算出圆的面积和半径的关系 参考技术D 圆周率＝圆的周长÷圆的直径　　
或
圆周率＝圆的面积÷圆的半径的平方