AVL树和红黑树的模拟实现

Posted 2022-09-17 玄鸟轩墨

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了AVL树和红黑树的模拟实现相关的知识，希望对你有一定的参考价值。

写在前面

我们要遇到C++里面最难一部分了,也是一些大厂有可能出的面试题,比如说手撕一个红黑树.这个博客的内容可能有点耗脑,我尽量和大家分享的接地气一点.

AVL 树

这种树也叫做平衡二叉树.这个是前面二叉搜索树的变种.我们前面谈过,对于比较有序元素,那么搜索二叉树就有点深了,甚至转换成了单只树,那么这样查找的效率就有点低了.所以我们提出的AVL树.所谓的平衡二叉树就是当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度 .这个就是AVL树的定义,至于如何做到,这里我们先不用关心.

我们先来看一下AVL树的特点,一般情况而言,对于那些比较有序的元素,我们插入元素后通过一系列的手段来降低树的高度,并且最后的树仍旧符合二叉搜索树的特点.

AVL树和红黑树的模拟实现_搜索二叉树

AVL树实现

我们已经知道AVL树是什么了,今天我们就要把他给简单的实现出来.这个过程说实话有点难.我们这里实现KV模型的．不过我们们先来把框架给搭出来.

namespace bit

  template<class T,class T>
  class AVLTree
  

  ;

平衡因子

我们前面把大的框架搭出来了,这里就需要开始搭建树的节点了,我们先暂时看一下,后面完善.这里我们已经搭建出来了,我们为何会加入父节点这个原因我们等到用到的时候再说.

struct AVLTreeNode

    AVLTreeNode(const T& data = T())
        : _praent(nullptr)
        , _left(nullptr)
        , _right(nullptr)
        , _data(data)
         

    AVLTreeNode<T>* _praent;
    AVLTreeNode<T>* _left;
    AVLTreeNode<T>* _right;

    T _data;
;

现在我们需要在谈一个问题,我们是如何确保左右节点的差距只有一呢?这里需要借助一个平衡因子,父节点的平衡因子记录左右子树高度的差值.这样我们插入的时候就可以看平衡因子的改变,从而判断是不是要移动树了.这里我们平衡因子记录的是右子树减去左子树.至于如何修改平衡因子的值这就有说道了.

AVL树和红黑树的模拟实现_搜索二叉树_02

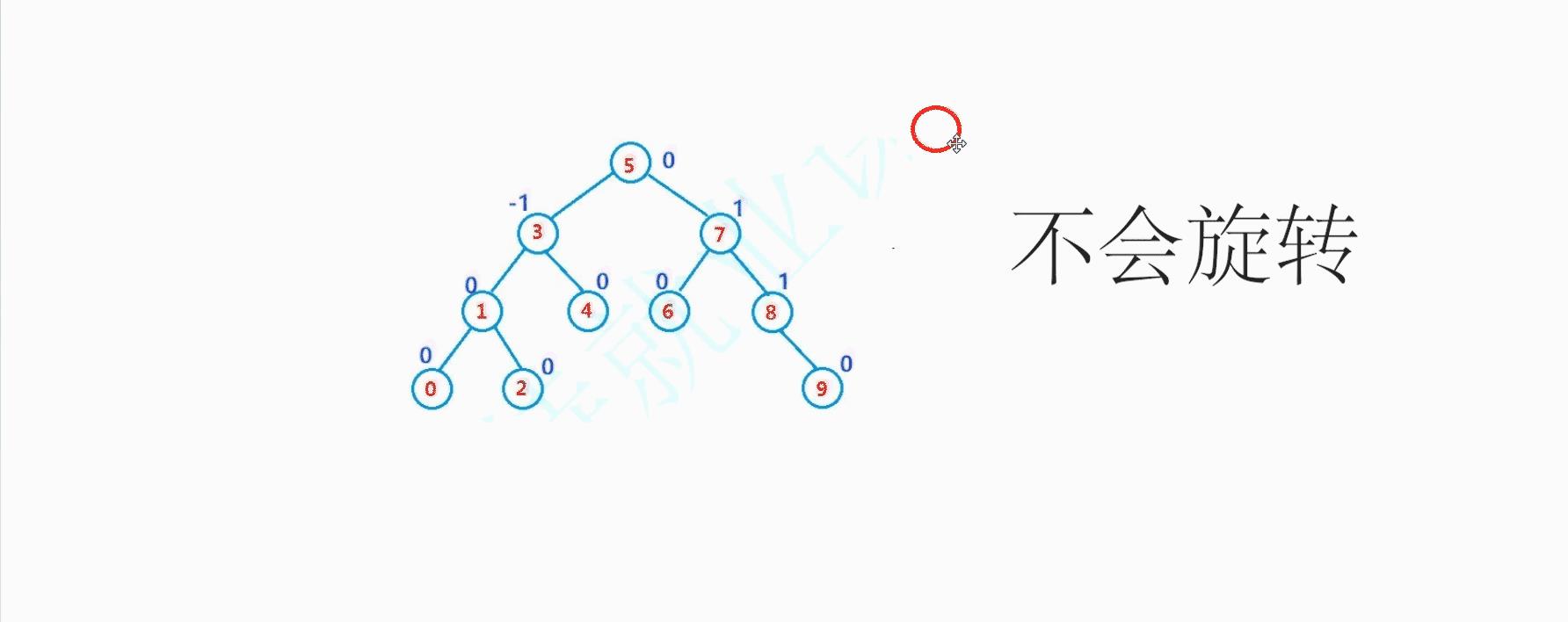
template<class T>
struct AVLTreeNode

    AVLTreeNode(const T& data = T())
        : _praent(nullptr)
        , _left(nullptr)
        , _right(nullptr)
        , _data(data)
        , _bf(0)
     

    AVLTreeNode<T>* _praent;
    AVLTreeNode<T>* _left;
    AVLTreeNode<T>* _right;

    T _data;
    int _bf;

;

插入元素

现在的的我们大框架已经打好了,我们现在开始重点的工作,这个可是比较烧脑的.我们也是只实现插入操作.

template<class T>
struct AVLTreeNode

    AVLTreeNode(const T& data = T())
        : _praent(nullptr)
        , _left(nullptr)
        , _right(nullptr)
        , _data(data)
        , _bf(0)
     

    AVLTreeNode<T>* _praent;
    AVLTreeNode<T>* _left;
    AVLTreeNode<T>* _right;

    T _data;
    int _bf;

;
template<class K, class T>
class AVLTreeV

    public:
    typedef AVLTreeNode<T> Node;
    AVLTree()
        :_pRoot(nullptr)
    

    bool Insert(const T& data)
    
        return true;
    
    public:
    Node* _pRoot;
;

首先第一步是简单的搜索二叉树的简单操作.我们先来找到插入的节点在哪里.

bool Insert(const T& data)

    // 第一步 判断 第一次 插入
    if (_pRoot == nullptr)
    
        _pRoot = new Node(data);
        _pRoot->_bf = 0;
        return true;
    

    // 第二步 搜索二叉树 找位置
    Node* cur = _pRoot;
    Node* parent = nullptr;
    while (cur != nullptr)
    
        if (cur->_data < data)
        
            // 去 右树 查找
            parent = cur;
            cur = cur->_right;
        
        else if (cur->_data > data)
        
            // 左树 查找
            parent = cur;
            cur = cur->_left;
        
        else
        
            // 我们这里不接受 重复值 ,你可以自己实现
            return false;
        
    

    // 第三步 new 出来一个节点
    Node* node = new Node(data);
    node->_bf = 0;               // 记住 不要相信构造函数,有可能不是你写的,不会自动默认0
    // 第四步 判断是插入左树还是 右树
    if (parent->_data > data)
    
        parent->_left = node;
    
    else
    
        parent->_right = node;
    
    // 这里需要链接
    node->_parent = parent;
    cur = node;
    // 更新平衡因子
    // ...
    return true;

我们这里预留了最关键的一步,就是更新平衡因子.这里需要讨论的事情是在是太多了.我们首先要判断是插入的节点是左树还是右树,这样方便我们修改父节点的平衡因子.

bool Insert(const T& data)

    // 第一步 判断 第一次 插入
    if (_pRoot == nullptr)
    
        _pRoot = new Node(data);
        _pRoot->_bf = 0;
        return true;
    

    // 第二步 搜索二叉树 找位置
    Node* cur = _pRoot;
    Node* parent = nullptr;
    while (cur != nullptr)
    
        if (cur->_data < data)
        
            // 去 右树 查找
            parent = cur;
            cur = cur->_right;
        
        else if (cur->_data > data)
        
            // 左树 查找
            parent = cur;
            cur = cur->_left;
        
        else
        
            // 我们这里不接受 重复值 ,你可以自己实现
            return false;
        
    

    // 第三步 new 出来一个节点
    Node* node = new Node(data);
    node->_bf = 0;               // 记住 不要相信构造函数,有可能不是你写的,不会自动默认0
    // 第四步 判断是插入左树还是 右树
    if (parent->_data > data)
    
        parent->_left = node;
    
    else
    
        parent->_right = node;
    
    // 这里需要链接
    node->_parent = parent;
    cur = node;
    // 更新平衡因子
    while (parent != nullptr)
    
        // 如果 插入的是 右子树
        if (cur == parent->_right)
        
            parent->_bf++;
        
        else
        
            parent->_bf--;
        

        //  开始 检测
        if (parent->_bf == 0)
        
            break;
        
        else if (parent->_bf == 1 || parent->_bf == -1)
        
            cur = parent;
            parent = parent->_parent;
        
        else if (parent->_bf == 2 || parent->_bf == -2)
        
            // 这里 才是 大头
            if (cur->_bf == 1 && parent->_bf == 2)
            
            
            else if (cur->_bf == -1 && parent->_bf == -2)
            
            
            // ...
        
        else
        
            assert(false);
        
    

    return true;

前面我们简单的叙述了一下平衡因子的改变,这里具体情况分析一下.首先,我们是按照祖先来更新的,这一点无可置疑

if (cur == prev->_right)

    prev->_bf++;

else

    prev->_bf--;

也就说我们修改平衡因子,当我们子树的高度没变,也就是平衡因子为0的时候,停止更新.要是高度变了,变成了1那么肯定是右子树的高度变高了,这就需要我们继续往上面走,要是-1,是左树树高了,也要往上面走.这里最关键的就是-2和2,这个是我们要谈的重点,也是我们需要旋转的条件.

左单旋

假设右子树比左子树高了两个,而且还满足一定的情况,我们这就使用左单旋.我们先来分析一下情况.

AVL树和红黑树的模拟实现_子树_03

至于如何旋转我们先暂时不谈,先来说几个具体的情况.

当 h = 0时

AVL树和红黑树的模拟实现_父节点_04

当 h = 1 时

AVL树和红黑树的模拟实现_父节点_05

当h = 2的时候这里的情况可就多了.

AVL树和红黑树的模拟实现_子树_06

我们就不往后面分析了,这里说一下具体的用法,还是按照理论来进行旋转.

AVL树和红黑树的模拟实现_父节点_07

把subRL给成parent的右子树
把parent 给成subL的左子树
修改逻辑顺序和平衡因子

AVL树和红黑树的模拟实现_父节点_08

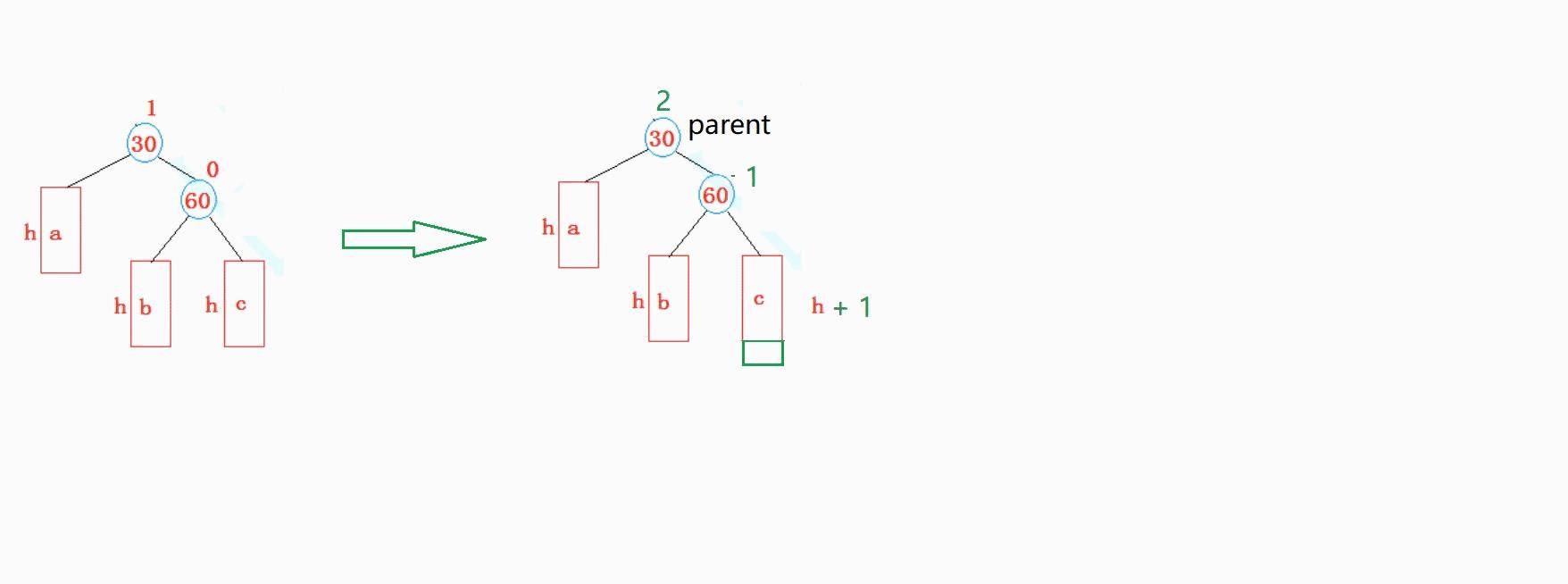
if (cur->_bf == 1 && parent->_bf == 2)

    // 左旋
    RotateL(parent);


void RotateL(Node* parent)

    Node* subR = parent->_right;
    Node* subRL = subR->_left;

    parent->_right = subRL;
    if(subRL)
        subRL->_praent = parent;
    // 记录 祖父节点
    Node* grandparent = parent->_praent;

    parent->_praent = subR;
    subR->_left = parent;

    if (grandparent == nullptr)
    
        // parent 就是 根节点
        _pRoot = subR;
        _pRoot->_praent = nullptr;
    
    else
    
        subR->_praent = grandparent;
        // 在判断  原本 的父节点 和 祖父的关系
        if (parent == grandparent->_left)
        
            grandparent->_left = subL;
        
        else
        
            grandparent->_right = subL;
        
    

    // 修改 平衡因子
    subR->_bf = 0;
    parent->_bf = 0;

我们先来把特殊的情况给分析一下,subRL可能为空,也就是h=0,这就造成subRL修改父节点的时候需要判断一下,还有就是你不感觉我们太顺风顺水了吗,你是如何确定parent一定是根节点的,我们前面的模型是一个子树的模型,不一定确保是完整的树.这个问题还是要判断的,否则就会出现问题.

右单旋

这个就比较简单了,我们这里直接上模型吧.右单旋就是右边高,这里需要向右边移动.

AVL树和红黑树的模拟实现_子树_09

AVL树和红黑树的模拟实现_搜索二叉树_10

else if (cur->_bf == -1 && parent->_bf == -2)

    // 右旋
    RotateR(parent);
    break;


void RotateR(Node* parent)

    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    parent->_left = subLR;
    if (subLR)
        subLR->_parent = parent;
    Node* grandparent = parent->_parent;
    parent->_parent = subL;
    subL->_right = parent;

    if (grandparent == nullptr)
    
        _pRoot = subL;
        _pRoot->_parent = nullptr;
    
    else
    
        subL->_parent = grandparent;
        if (grandparent->_left == parent)
        
            grandparent->_left = subL;
        
        else
        
            grandparent->_right = subL;
        
    
    // 更新平衡因子
    subL->_bf = parent->_bf = 0;

我们先来测试一下单旋,也就是我们尽量插入有序的元素,这里就只需要单旋操作.但是这里我们需要注意,这里我们可不是能够确定我们的树是AVL树，只是看看我们代码是不是和逻辑符合．

void test1()

    AVLTree<int, int> a;
    for (int i = 0; i < 8; i++)
    
        a.Insert(i+1);
    
    cout << "层序遍历" << endl;
    a.levelOrder();
    cout << "中序遍历" << endl;
    a.inorder();

AVL树和红黑树的模拟实现_父节点_11

左右双旋

现在我们开始一个比较复杂的情况,是双旋的问题.我们要是直接插入8,6,7.这就有意思了.看一下.你会发现简单的单旋是解决不了问题的.这里需要一点手段.

AVL树和红黑树的模拟实现_父节点_12

我们先来看一下模型吧,后面在讨论解决方案.这里就像是一个折线图.

AVL树和红黑树的模拟实现_搜索二叉树_13

这里我们也列举几个具体的情况.

AVL树和红黑树的模拟实现_父节点_14

这个时候我们就在想,这个应该如何旋转,这里需要一点变通.我们先来看大方针.

AVL树和红黑树的模拟实现_父节点_15

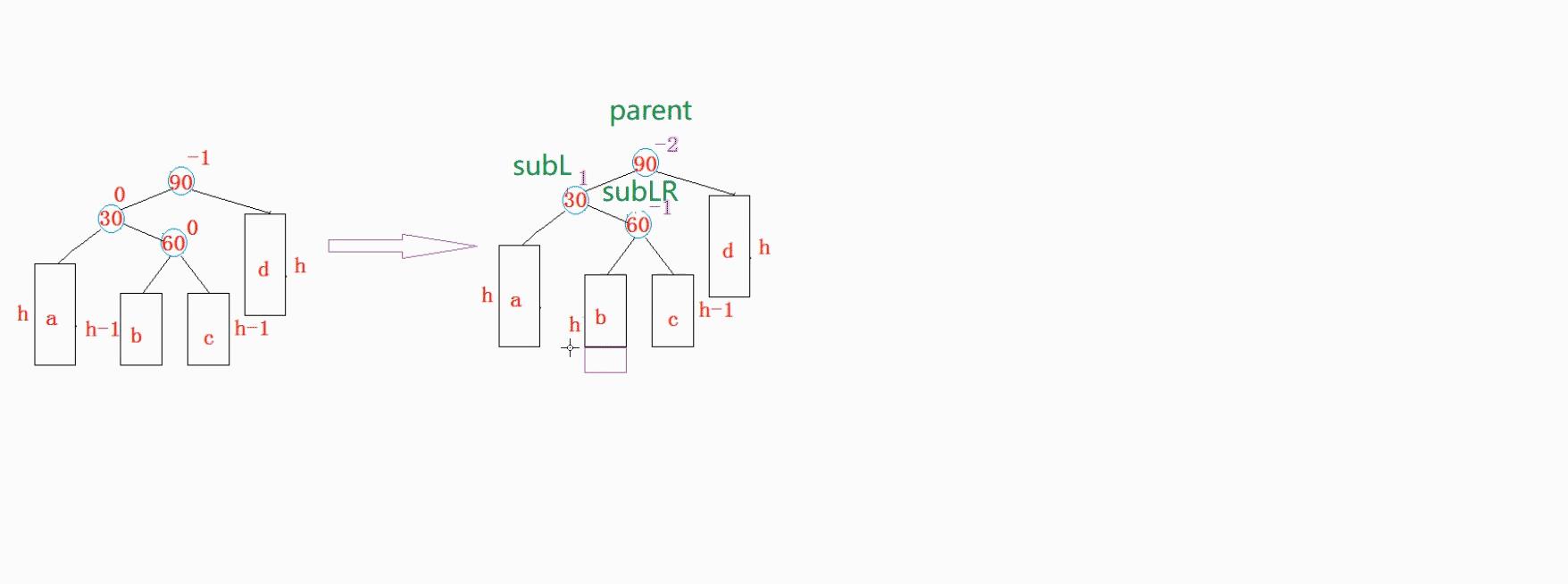
也就是说我们需要以subL做左单旋,后面以parent做右单旋.

else if (cur->_bf == 1 && parent->_bf == -2)

    RotateLR(parent);
    break;

void RotateLR(Node* parent)

    RotateL(parent->_left);
    RotateR(parent);
    // 修改平衡因子
    // ...

注意我们旋转是没有问题的,这里可以直接复用前面的,难的是需要修改平衡因子.那么这里面就存在下面的问题,看一看下面的方法

AVL树和红黑树的模拟实现_子树_16

我们需要把这些节点给保存下来,而且还要讨论如何给这些节点修改平衡因子.

void RotateLR(Node* parent)

    Node* subL = parent->_left;
    Node* subLR = subL->_right;

    RotateL(parent->_left);
    RotateR(parent);
    // 修改平衡因子
    // ...

现在我们剩下的问题就是如何修改平衡因子了,我们知道subLR一定是0,但是subL和parent可就不一定了,这需要分情况讨论,那么我们讨论的依据是什么呢?这就有点意思了.我们根据苏subLR的平衡因子的值来讨论.不过我们需要先把它给记录下来,单旋的时候会把它给修改了.我们根据下面的图来修改就可以了.

AVL树和红黑树的模拟实现_搜索二叉树_17

void RotateLR(Node* parent)

    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    int bf = subLR->_bf;
    RotateL(parent->_left);
    RotateR(parent);
    // 修改平衡因子
    if (bf == 0)
    
        parent->_bf = 0;
        subL->_bf = 0;
        subLR->_bf = 0;
    
    else if (bf == 1)
    
        parent->_bf = 0;
        subL->_bf = -1;
        subLR->_bf = 0;
    
    else if (bf == -1)
    
        parent->_bf = 1;
        subL->_bf = 0;
        subLR->_bf = 0;
    
    else
    
        assert(false);

右左双旋

这个和上面的是一样的,也是折线,我们是需要右单旋加上左单旋.

AVL树和红黑树的模拟实现_搜索二叉树_18

看下解决思路,我这里就不具体的举例子了.

AVL树和红黑树的模拟实现_父节点_19

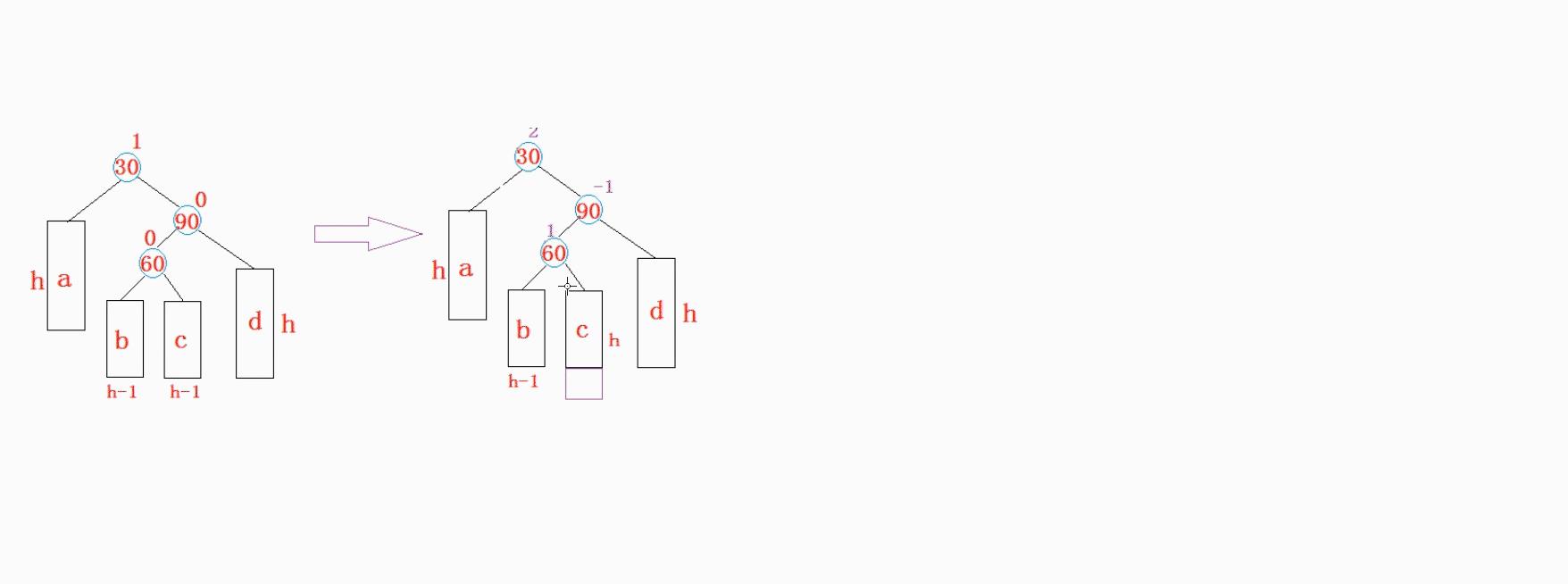
else if (cur->_bf == -1 && parent->_bf == 2)

    RotateRL(parent);
    break;

void RotateRL(Node* parent)

    Node* subR = parent->_right;
    Node* subRL = subR->_left;
    int bf = subRL->_bf;

    RotateR(parent->_right);
    RotateL(parent);

    // 修改平衡因子

我么还是重点关注如何修改平衡因子,这个需要简单的分析一下,但是思路和上面都是一样的.

AVL树和红黑树的模拟实现_搜索二叉树_20

void RotateRL(Node* parent)

    Node* subR = parent->_right;
    Node* subRL = subR->_left;
    int bf = subRL->_bf;

    RotateR(parent->_right);
    RotateL(parent);

    // 修改平衡因子
    if (bf == 0)
    
        subR->_bf = 0;
        parent->_bf = 0;
        subRL->_bf = 0;
    
    else if(bf == 1)
    
        subR->_bf = 0;
        parent->_bf = -1;
        subRL->_bf = 0;
    
    else if (bf == -1)
    
        subR->_bf = 1;
        parent->_bf = 0;
        subRL->_bf = 0;
    
    else
    
        assert(false);

我们这里也测试一下乱序的情况,避免代码出现错误.

void test2()

    int arr[] =  1,4,3,7,5,8,1,10 ;
    int sz = sizeof(arr) / sizeof(arr[0]);
    AVLTree<int, int> a;
    for (int i = 0; i < sz; i++)
    
        a.Insert(arr[i]);
    
    cout << "层序遍历" << endl;
    a.levelOrder();
    cout << "中序遍历" << endl;
    a.inorder();

AVL树和红黑树的模拟实现_子树_21

AVL树的判定

这里我们需要看看自己写的AVL树到底是不是正确的,这里直接上代码.

public:
    bool isBalanceTree()
    
        return _IsBalanceTree(_pRoot);
    
private:
    int _height(Node* root)
    
        if (root == nullptr)
            return 0;

        int lh = _height(root->_left);
        int rh = _height(root->_right);

        return lh > rh ? lh + 1 : rh + 1;
    
    bool _IsBalanceTree(Node* root)
    
        // 空树也是平衡二叉树
        if (root == nullptr)
            return true;

        // 记录 左右节点的高度
        int left = _height(root->_left);
        int right = _height(root->_right);
        int diff = left - right;
        // 判断 平衡因子
        if (abs(diff) >= 2)
        
            cout << "平衡因子更新错误" << endl;
            return false;
        
        if (right - left != root->_bf)
        
            cout << "节点平衡因子不符合实际" << endl;
            return false;
        
        return _IsBalanceTree(root以上是关于AVL树和红黑树的模拟实现的主要内容，如果未能解决你的问题，请参考以下文章 
 二叉树和红黑树
 红黑树和AVL树的区别（转）
 红黑树的变换
 高级树AVL 树和红黑树
 排序二叉树，平衡二叉树和红黑树的概念以及相关的操作讲解
 红黑树插入删除详细步骤动画演示与AVL树的区别