深度学习中常用的几种卷积（上篇）：标准二维卷积转置卷积1*1卷积（附Pytorch测试代码）

Posted 2022-09-07 NorthSmile

卷积分类

• 一、标准二维卷积
• • 1.卷积核和过滤器
  • 2.标准二维卷积
  • 3.调用方式
  • 4.实例
• 二、1×1卷积
• • 1.介绍
  • 2.实例
• 三、转置卷积（去卷积）
• • 1.介绍
  • 2.调用方式
  • 3.实例
  • 4.缺点
• 参考资料

膨胀卷积、可分离卷积等详见下篇： https://blog.csdn.net/qq_43665602/article/details/126708012。

一、标准二维卷积

在图像处理中，卷积操作实际是对于输入特征与卷积核之间的一个“加权求和”的过程，下图可以直观的解释这个过程：蓝色代表（1，5，5）输入特征，采用（1，3，3）卷积核，卷积核从输入的左上角开始沿着W和H的方向进行卷积操作，每一次卷积其实就是卷积核对应于输入的特征之间进行元素乘法，然后将进行元素加法，最后得到灰色的（1，3，3）输出。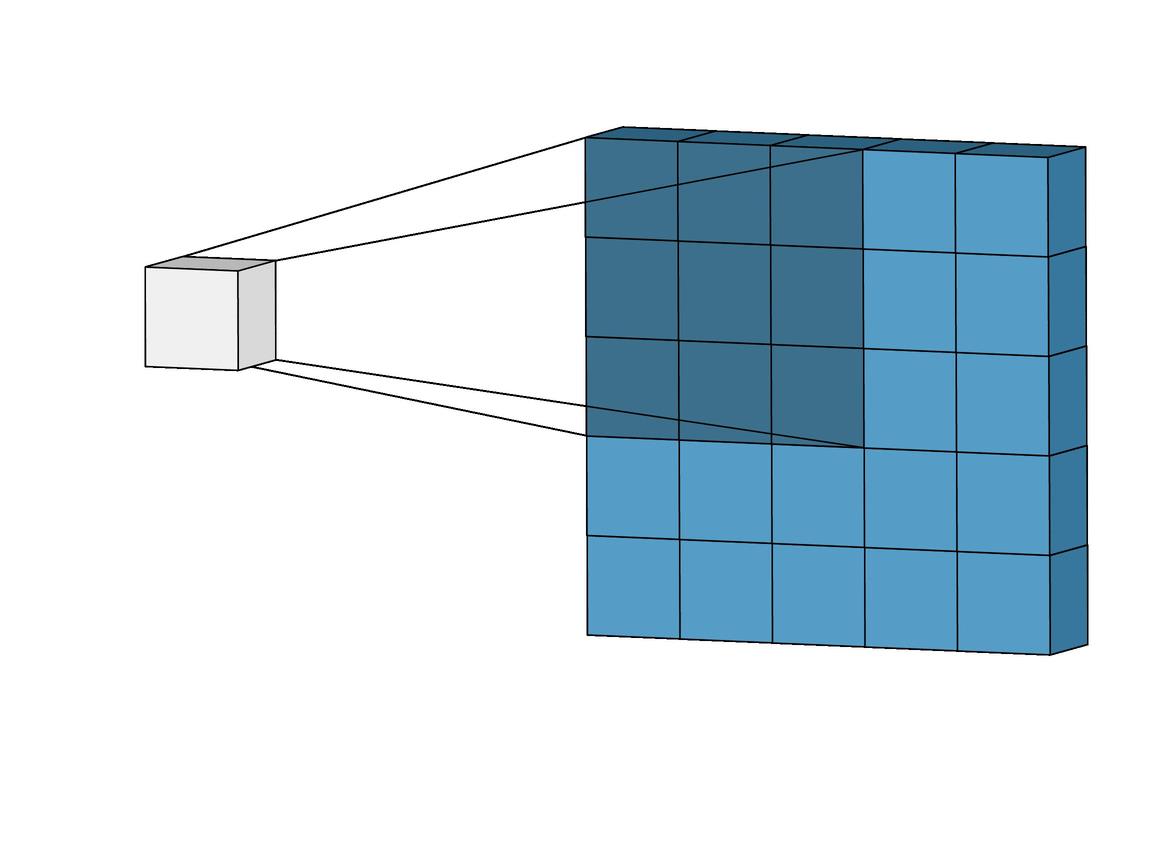
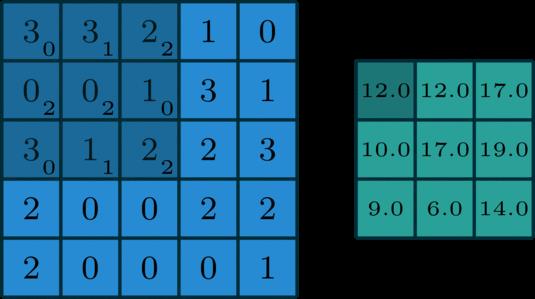
下图蓝色表示输入，绿色表示输出，卷积核为：
卷积核每次移动得到一个值，比如输出中的左上角元素12=3×0+3×1+2×2+0×2+0×2+1×0+3×0+1×1+2×2

1.卷积核和过滤器

（1）卷积核：指定大小、由权重组成的二维数组，如下图：

（2）过滤器：一组卷积核叠加在一起的三维数据，如下图：
通常在神经网络卷积层中，过滤器由一组指定大小的卷积核叠加组成。在标准二维卷积中，该过滤器所含卷积核的个数和输入特征的通道数保持一致，该网络层的输出通道数指的是该层所采用过滤器的个数。比如，layer1的输入为（N，128，H，W），卷积核为（3，3），输出为（N，256，H1，W1），则表示layer1网络层中采用256个过滤器，每个过滤器包含128个3*3的卷积核。

2.标准二维卷积

深度学习中神经网络的输入或输出通常都是形状为（N，C，H，W）的多通道特征图，就该批次特征中的每一个特征映射来说，他们均是形状为（C，H，W）的三维数据。我们知道对这样的数据进行卷积处理时，根据卷积核的移动方式可分为：
1）三维卷积（3D卷积）
此时，过滤器所含卷积核数小于输入特征通道数，网络层所采用的3D过滤器可以沿着输入特征的高、宽、通道的方向移动，每个过滤器在3D空间移动，每次移动的卷积结果为一个值，所有卷积结果以3D数据形式体现。所有过滤器的卷积结果均为一个3D数据，将他们的结果沿着通道的方向叠加起来即为该3D卷积层最后的输出结果。

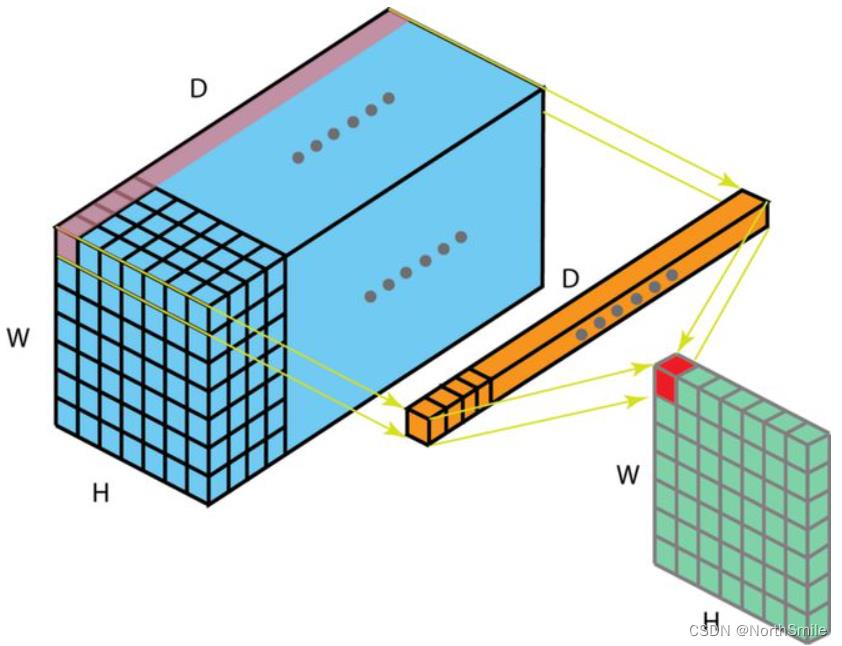
图中黄色填充的3D数据即是3D卷积所采用的滤波器，该滤波器由3个卷积核叠加而来，可沿着蓝色输入的高、宽和通道方向移动，每次移动会进行卷积得到一个数字，对应绿色输出中的一个元素。每个滤波器会得到如图所示的3D绿色输出。
2）二维卷积（2D卷积）
此时，过滤器所含卷积核数等于输入特征通道数，网络层所采用的3D过滤器只能沿着输入特征的高、宽的方向移动。每个过滤器最后的输出为一个单通道数据，将所有过滤器的卷积结果沿着通道的方向叠加起来即为该2D卷积层最后的输出结果。因为二维卷积只能在输入的3D数据上沿着高和宽两个方向移动，因此一般将他称为二维卷积，也是图像处理中最常用的标准二维卷积。

图中黄色填充的3D数据即是2D卷积所采用的滤波器，该滤波器所含卷积核数量与蓝色输入通道数一致，只可沿着蓝色输入的高和宽方向移动，每次移动会进行卷积得到一个数字，对应绿色输出中的一个元素。每个滤波器最后可得到图中所示的一维绿色数据。

3.调用方式

• 对输入向量做2维卷积操作；
• 输入形状：(N,C_in,H_in,W_in)或(C_in,H_in,W_in)；
• 输出形状：(N,C_out,H_out,W_out)或(C_out,H_out,W_out)；其中：
  

torch.nn.Conv2d(
	in_channels, 
	out_channels, 
	kernel_size, 
	stride=1, 
	padding=0, 
	dilation=1, 
	groups=1, 
	bias=True, 
	padding_mode='zeros', 
	device=None, 
	dtype=None)

参数解析：

参数名	含义
in_channels	输入特征的通道数
out_channels	过滤器的数量：卷积层期望输出结果的通道数
kernel_size	卷积核尺寸：整数Kernel_H或2元组（Kernel_H,Kernel_W）
stride	卷积核移动的步长：整数Stride_H或2元组（Stride_H,Stride_W）
dilation	膨胀率：决定卷积核每个元素之间的距离，默认为1；可为整数Dilation_H或2元组（Dilation_H,Dilation_W）。详见膨胀卷积。
padding	所需填充的大小：可为整数Padding_H或2元组（Padding_H,Padding_W）
padding_mode	填充方式：可选’zeros’, ‘reflect’, ‘replicate’ ， ‘circular’；默认’zeros’

注意：

• ‘zeros’, ‘reflect’, ‘replicate’ ， 'circular’分别表示填充方式为：全零填充、反射填充、复制填充和循环填充；
• padding默认为0，表示不进行填充，与padding='valid’等价；
• groups参数主要应用在分组卷积和深度可分离卷积中，详见https://blog.csdn.net/qq_43665602/article/details/126708012
• 步长为1，padding='same’表示进行全零填充，此操作可保持特征图大小不变；
• kernel_size, stride, padding, dilation均支持两种形式，当为单一整数时表示高度、宽度设置同样大小；为2元组（H,W）时，表示对高度、宽度分别设置指定大小；
• 在指定padding大小的时候，可以根据上面的公式通过输入、输出的大小计算合适的padding：
  
  

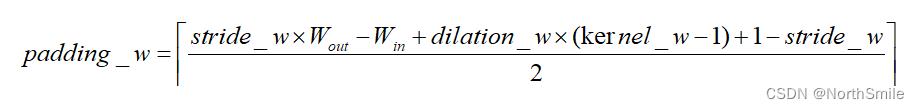
4.实例

inp_tensor=torch.tensor([[[[3., 6., 6., 8., 7.],
          [9., 2., 4., 4., 9.],
          [5., 7., 3., 0., 0.],
          [8., 6., 1., 1., 9.],
          [7., 5., 3., 8., 6.]]]])
print('-'*25)
conv2d=nn.Conv2d(
    in_channels=1,
    out_channels=1,
    kernel_size=3,
    stride=2,
)
out_tensor=conv2d(inp_tensor)
print(out_tensor)
print(out_tensor.shape)
print('-'*25)
print(conv2d.weight)
print(conv2d.weight.shape)
print('-'*25)
print(conv2d.bias)
print(conv2d.bias.shape)
print('-'*25)

输出：
tensor([[[[ 0.4838, -1.0925],
          [ 0.8192,  2.4081]]]], grad_fn=<ThnnConv2DBackward>)
torch.Size([1, 1, 2, 2])
-------------------------
卷积核：
Parameter containing:
tensor([[[[ 0.2619, -0.2953, -0.0338],
          [ 0.0633,  0.1857, -0.0656],
          [-0.2118,  0.2236,  0.1076]]]], requires_grad=True)
torch.Size([1, 1, 3, 3])
-------------------------
偏置：
Parameter containing:
tensor([0.1647], requires_grad=True)
torch.Size([1])
-------------------------

二、1×1卷积

1.介绍

1×1卷积与上一节介绍的2D卷积差别仅在于，1×1卷积的卷积核大小是（1,1）。

1×1卷积通常用于：
（1）特征降维：可通过调整卷积步长、过滤器数量来进行特征降维，降低计算量；
（2）引入非线性：通过在学习中引入非线性激活函数，扩大网络的假设空间，增强网络的学习能力。

2.实例

inp_tensor=torch.randint(10,size=(1,6,5,5),dtype=torch.float32)
print(inp_tensor.shape)  # (1,6,5,5)
# print(inp_tensor)
conv2d=nn.Conv2d(
    in_channels=6,
    out_channels=3,
    kernel_size=1,
    stride=2
)
out_tensor=conv2d(inp_tensor)
# print(out_tensor)
print(out_tensor.shape)
print(conv2d.weight.shape)
print(conv2d.bias.shape)

torch.Size([1, 6, 5, 5])
torch.Size([1, 3, 3, 3])
torch.Size([3, 6, 1, 1])
torch.Size([3])

三、转置卷积（去卷积）

1.介绍

1）卷积通常是实现对特征图的下采样操作，所以为了对特征图进行上采样操作，提出和标准卷积相反的转置卷积，此操作可用于代替传统的插值方法实现上采样操作。
作用：

• 特征上采样；
• 将低维特征映射到高位空间；

通过对标准卷积的卷积核、步长、填充等参数进行合适的设置，可以实现转置卷积：
（1）输入：（1，2，2），kernel_size=3，padding=2，stride=1，dilation=1，则输出中：
H_out=floor((2+2×2-1×(3-1)-1)/1+1)=4，W_out=floor((2+2×2-1×(3-1)-1)/1+1)=4

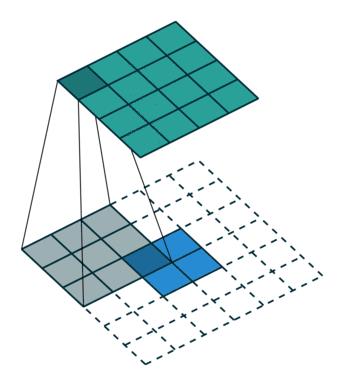
（2）输入：（1，2，2），并在元素之间填充一个空格，形成伪输入：（1，3，3），kernel_size=3，padding=2，stride=1，dilation=1，则输出中：
H_out=floor((3+2×2-1×(3-1)-1)/1+1)=5，W_out=floor((3+2×2-1×(3-1)-1)/1+1)=5

2）转置卷积名字由来
我们常在论文中看到deconvolution（去卷积），但在信号/图像处理中对于去卷积的定义是卷积的逆运算，此处并不是，而只是标准卷积的一个反向操作，常用于实现特征上采样，一般将此操作称为转置卷积更合适。
此处举个例子更直观看到所谓的“转置“从何体现，已知输入、输出以及卷积核均为特定形状的矩阵，故可以从矩阵相关性质去解释，假设卷积核为（3,3）矩阵C，输入为（4,4）矩阵X，输出为（2，2）矩阵Y：
（0）矩阵相关性质（此处指实数矩阵）：

• 矩阵A、矩阵B可进行矩阵乘法AB的前提是：A的列数=B的行数；

（1）标准卷积：标准卷积通常用于下采样，通过卷积核和输入特征之间的互相关操作得到尺寸更小的输出，从矩阵的角度来看卷积核和输入特征对应的矩阵通过矩阵乘法实现下采样操作。具体地，卷积核定义了网络前向传播、反向传播需要的矩阵C以及转置矩阵T（C)，先将卷积核转换为合适的（4，16）稀疏矩阵C，将输入、输出分别按行展开为（16，1）矩阵X，（4，1）矩阵Y，可见CX=Y。

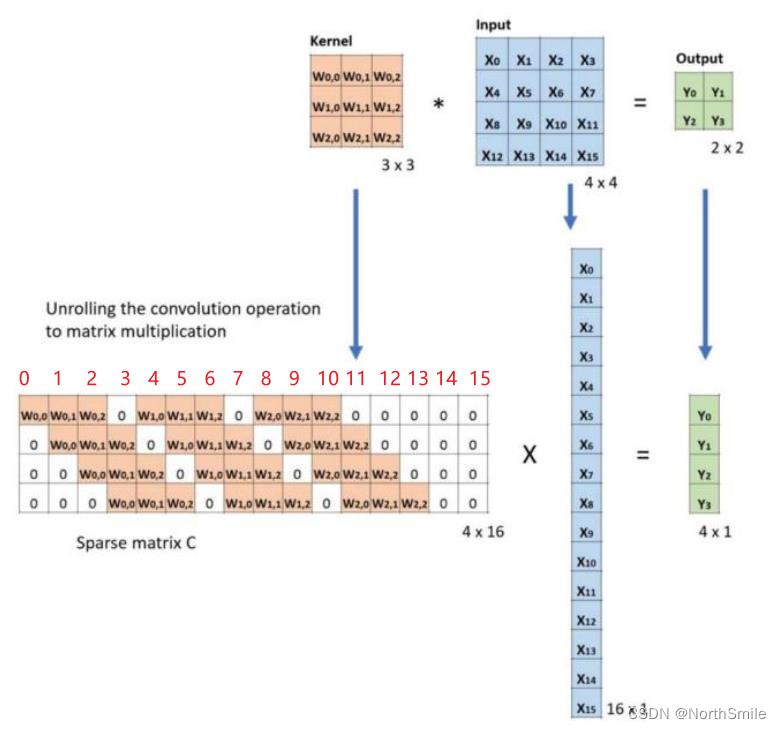
（2）转置卷积：转置卷积通常用于上采样，通过卷积核和输入特征之间的互相关操作得到尺寸更大的输出，从矩阵的角度来看卷积核利用转置矩阵和输入特征对应的矩阵通过矩阵乘法实现上采样操作。具体地，卷积核定义了网络前向传播、反向传播需要的转置矩阵T（C)以及矩阵C，转置卷积以小尺寸（4，1）矩阵Y作为输入，与（16，4）稀疏矩阵T（C)进行矩阵乘法，输出大尺寸（16，1）矩阵X。由此可看到在实现此卷积操作时利用卷积核的转置进行矩阵乘法，这也是转置卷积的由来。

更多内容见：https://arxiv.org/abs/1603.07285第四章内容

2.调用方式

• 对输入向量做2维转置卷积操作；
• 输入形状：(N,C_in,H_in,W_in)或(C_in,H_in,W_in)；
• 输出形状：(N,C_out,H_out,W_out)或(C_out,H_out,W_out)；其中：
  

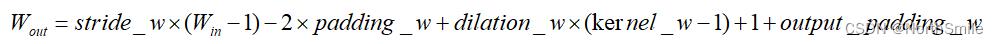
torch.nn.ConvTranspose2d(
	in_channels, 
	out_channels, 
	kernel_size, 
	stride=1, 
	padding=0, 
	output_padding=0, 
	groups=1, 
	bias=True, 
	dilation=1, 
	padding_mode='zeros', 
	device=None, 
	dtype=None)

转置卷积与标准卷积在调用时参数设置及含义类似，区别在于：

参数名	含义
stride	卷积步长：在这是指输入中每个元素之间的距离；如果输入为（2,2），stride=2，则表示输入此时拥有（3,3）大小。
padding	对输入进行dilation * (kernel_size - 1) - padding的全零填充
output_padding	对输出结果附加的尺寸，默认为0；只用于确定输出尺寸，不是对输出结果进行全零填充
padding_mode	转置卷积只支持全零填充

转置卷积在调用时如果所有参数设置的大小与标准卷积设置一致，那么就他们的输入和输出形状而言，二者可逆。比如，标准卷积输入为（5，5），卷积核为（3，3），则输出为（3,3）；对应的，转置卷积输入为（3，3），卷积核为（3，3），先对输入进行（3-1,3-1）=（2,2）填充得到伪输入（7,7），则输出为（5,5）。

3.实例

1）二维转置卷积：展示卷积过程

# torch.Size([1, 1, 2, 2])
inp=torch.tensor([[[[9., 8.],
          [3., 8.]]]])
# print(inp.shape)
# print(inp)
print('-'*25)
conv_trans1=nn.ConvTranspose2d(
    in_channels=1,
    out_channels=1,
    kernel_size=(3,3),
    stride=2,
    padding=0,
    output_padding=0,
)
out1=conv_trans1(inp)
print(out1.shape)
# print(out1)
print('-'*25)
# print(conv_trans1.weight)
print(conv_trans1.weight.shape)
# print(conv_trans1.bias)
print(conv_trans1.bias.shape)

输入为（2，2），卷积核为（3，3），stride=1说明输入元素之间距离为1，先对输入进行（3-1,3-1）=（2,2）填充得到伪输入（6,6），则输出为（4,4）。

stride=1时：
-------------------------
torch.Size([1, 1, 4, 4])
-------------------------
torch.Size([1, 1, 3, 3])
torch.Size([1])

输入为（2，2），卷积核为（3，3），stride=2说明输入元素之间距离为2，输入拥有（3,3）大小，再对输入进行（3-1,3-1）=（2,2）填充得到伪输入（7,7），则输出为（5,5）。

stride=2时：
-------------------------
卷积结果：
torch.Size([1, 1, 5, 5])
tensor([[[[ 0.0260, -1.5984,  0.3259, -1.4333,  0.1680],
          [ 0.9724, -2.3583, -0.3488, -2.1087, -1.1796],
          [ 1.5210, -0.0468,  0.4571, -0.9347, -0.7827],
          [ 0.2492, -0.8610,  0.4517, -2.1087, -1.1796],
          [ 0.4167,  0.0746,  0.9420,  0.3862, -1.0630]]]],
       grad_fn=<SlowConvTranspose2DBackward>)
-------------------------
卷积核Weight：
Parameter containing:
tensor([[[[ 0.0154, -0.1651,  0.0350],
          [ 0.1205, -0.2495, -0.1334],
          [ 0.1764,  0.0623, -0.1188]]]], requires_grad=True)
torch.Size([1, 1, 3, 3])
偏置bias：
Parameter containing:
tensor([-0.1123], requires_grad=True)
torch.Size([1])

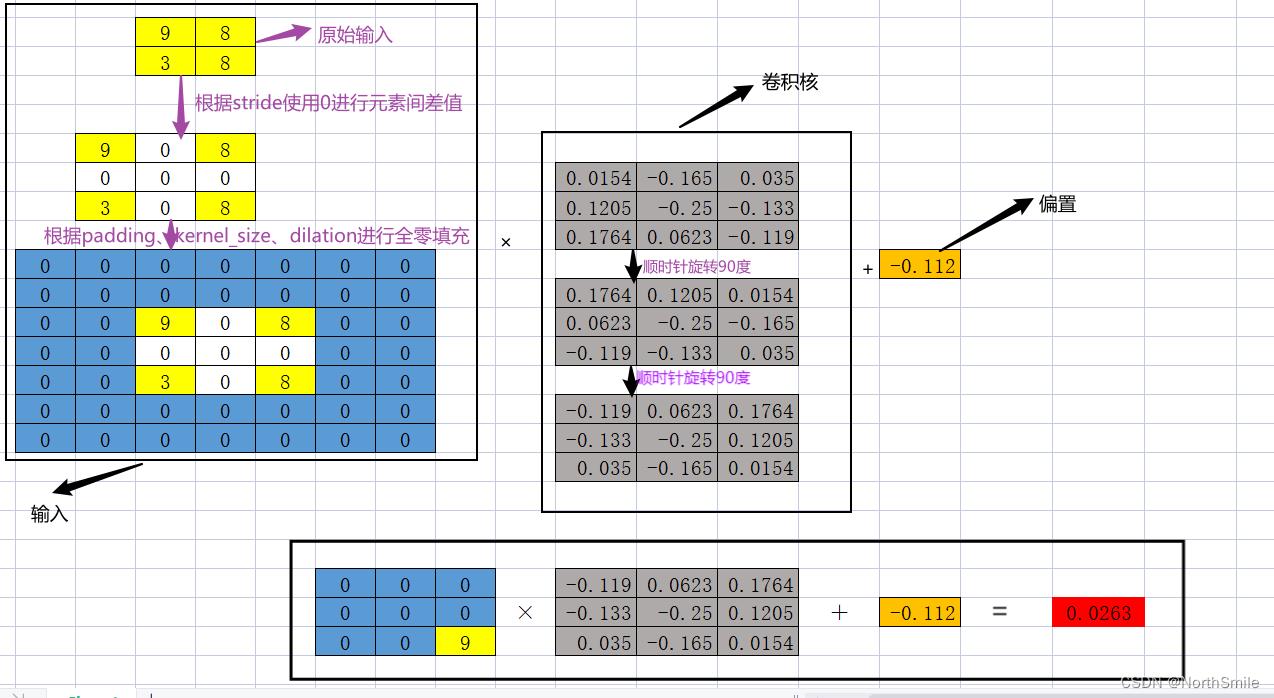
以输出中左上角第一个元素为例，展示卷积过程：

• 对原始输入用0按照stride进行插值，元素间距离为stride-1；
• 根据padding、kernel_size等参数对上述输入进行全零填充；
• 在可视化过程中，需将卷积核进行180度旋转；
• 按照标准卷积方式进行卷积操作；

2）一维转置卷积：验证output_padding参数
因为不同尺寸的输入通过给标准卷积设置合适的参数可以得到相同大小的输出，因此转置卷积作为标准卷积相反操作，对指定大小输入进行卷积可能会输出不同大小的特征，设置output_padding是为了消除这种模糊性，转置卷积在最后的输出结果的每个维度一个边进行填充。在实现时要注意output_padding必须小于stride或者dilation。比如此处stride=2，则output_padding可取0或1，output_padding=0时输出L_out=16，而out_padding=1时输出L_out=17。设置这些参数时主要还是根据你的期望输出大小，代入上面的计算公式中推出合适的参数。比如，输入L_in=8，stride=2，期望输出L_out=16，则可使其他参数保持默认，output_padding=0；而输入L_in=8，stride=2，期望输出L_out=17，则可使其他参数保持默认，output_padding=1；

inp=torch.randint(10,size=(1,1,8),dtype=torch.float32)
print(inp)
print(inp.shape)
print('-'*25)
conv_t=nn.ConvTranspose1d(
    in_channels=1,
    out_channels=1,
    kernel_size=2,
    stride=2,
    output_padding=1
)
out=conv_t(inp)
print(out)
print(out.shape)
print('-'*25)
print(conv_t.weight)
print(conv_t.bias)

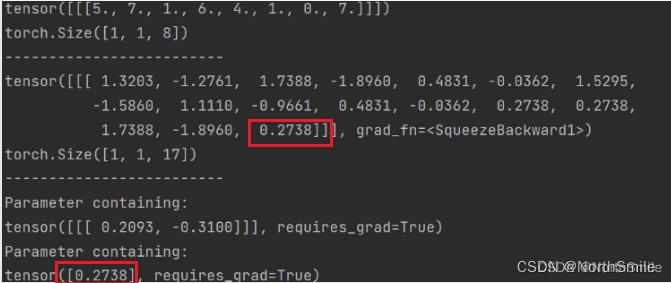
愣是没找到内部怎么去填充output_padding，多次代码测试发现转置卷积对最后的输出结果，按照outp_padding大小，使用该层偏置bias的值进行填充（二维转置卷积也是一样，采用bias的值进行填充）。

4.缺点

由于转置卷积的“不均匀重叠”，卷积结果经常会存在“棋盘伪影”，影响卷积效果。“棋盘伪影”详见https://blog.csdn.net/qq_43665602/article/details/126691423。

参考资料

1.部分图来源：
（1）https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
（2）https://www.163.com/dy/article/E8F50CLJ05118HA4.html
（3）https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md
2.参考：
https://www.163.com/dy/article/E8F50CLJ05118HA4.html
文章通过参考及自己理解汇总，如有错误，欢迎大家评论探讨！我会及时更正，谢谢。